-
随着我国城镇化和工业化进程的持续推进,生态破坏和环境污染逐步成为当下我国“不平衡”和“不充分”的重要表现,制约了经济和社会的可持续发展[1]。党的十八大以来,我国经济发展进入了“新常态”,经济发展模式逐步由高速发展向高质量发展转变,“绿水青山就是金山银山”等新时代发展理念逐步成为了全社会的共识[2]。因此,分析当前我国环境污染的现状,探寻不同影响因素对环境污染的驱动效应,进而提出改善生态环境的可行路径成为了学界和政界关注的重点问题[3]。长三角城市群是我国东部地区三大城市群(京津冀城市群、粤港澳大湾区和长三角城市群)之一,是探索经济可持续发展和区域一体化模式的龙头基地[4]。近年来,尽管政府对环境保护进行了强有力的干预,但人口的增长以及频繁的经济活动使得长三角城市群的空气污染、水污染和土壤污染等问题依旧严峻,亟需探索解决环境污染问题的办法[5]。相关研究表明,产业结构升级和技术创新会对污染物的排放和治理产生极大影响[6]。基于此,本文以长三角城市群为研究对象,通过空间分析技术探究长三角城市群的PM2.5空间分布特征,在此基础上从产业结构升级和技术改进视角分析长三角城市群缓解空气污染状况的实施路径。
本文的创新点主要体现在2个方面:一是研究方法的创新。不同于以往通过单个监测站点获得的数据对特定地域开展的相关研究,本研究使用面板数据可以对PM2.5污染扩散的规律进行较为全面和深入的研究。具体而言,基于跨越2007~2017年的PM2.5浓度数据集,本研究对长三角地区城市群PM2.5污染的时序演变和空间分布特征进行了比较、分析。在一般计量模型的基础上进行改进,本文使用动态空间面板模型量化了多种影响因素尤其是产业结构升级、技术进步以及两者的交互项对PM2.5污染的影响。二是研究视角上的创新,本文以产业结构和技术进步为切入点探究解决路径,相比于以往的研究,所提出的解决路径更具可实施性。
-
基于已有研究,本文建立常规面板模型,见式(1):
式中,Pp表示PM2.5污染,Is表示产业结构升级,Tp表示技术进步,Ed表示经济发展水平,Ul表示城市化水平,Tr表示交通密度,Te表示温度,Pr表示降水。β0表示回归常数项,β1~β7分别表示每个变量的回归系数,ε表示误差项。i涵盖长三角地区的26个城市,t的范围是2007~2017年。式(1)是一个一般化面板模型,它没有考虑PM2.5污染的动态效应和空间效应。鉴于有研究表明PM2.5污染确实存在显著的时序动态属性[1],因此应尝试将此效应纳入回归模型。本文将被解释变量即PM2.5污染的一阶滞后项纳入等式,建立了常规动态面板(ODP)模型,见式(2):
式中,τ表示PM2.5污染一阶滞后项的回归系数,反映了前期相关因素对当前时期PM2.5污染的影响。同理,如果仅考虑PM2.5污染的空间效应并将其空间滞后项纳入等式,建立静态空间面板(SSP)模型,见式(3~4):
式中,ρ和δ均为空间系数,反映了PM2.5污染差异化的空间溢出,即空间滞后和空间误差。Wij是一个地理权重矩阵,常用于表征地理单位的空间关联。本文基于地理距离来确定空间权重矩阵Wij,即wij=1/dij,其中dij代表地区i与地区j之间的欧几里得距离。综上,若同时考虑PM2.5污染的动态效应和空间效应,可以将PM2.5污染的一阶滞后项和空间滞后项同时纳入等式,建立动态空间面板(DSP)模型,见式(5~6):
-
由于统计数据中的空间自相关和空间异质性会影响回归系数和统计分析过程中的推论[2],因此,通常在执行计量经济学模型回归之前进行空间自相关检验。Moran’s I是目前使用最为广泛的空间自相关性分析方法,包括全局Moran’s I和局部Moran’s I。首先,根据公式使用全局Moran’s I测试全局空间自相关,见式(7):
式中,Global Moran’s I是全局Moran’s I指数,N表示地理单位即城市的总数,p表示城市i的PM2.5浓度,
$ \overline p $ 和S2分别表示城市总体PM2.5浓度的平均值和方差。另外,Z值作为一种检验全局Moran’s I指数显著性的统计量,见式(8~10):用于测试局部空间自相关的局部Moran’s I指数则可由以下公式获得。
-
PM2.5污染:为了得到城市PM2.5浓度历史数据,本文采用了达尔豪斯大学大气成分分析小组公布的全球平均PM2.5浓度的栅格数据[3]。该栅格数据是使用地球物理统计方法结合卫星、模型和监测器的信息计算得出。本文将ArcGIS10.5与中国市一级行政矢量图相结合,对栅格数据分解和地区裁剪获得长三角城市群2007~2017年的PM2.5年均浓度数据并以此衡量PM2.5污染。
-
产业结构升级:区域产业结构的升级是指要素禀赋从生产效率低的产业部门向生产效率高的产业部门转移的过程。目前,学者们还没有形成一个衡量产业结构升级的统一标准。现有大多数研究基于三大产业中产值和就业的百分比或者通过构建综合指标体系来计算产业结构升级的指数[4-5]。本文参考CHENG et al[6]的研究,使用区域第三产业的产值比例表征产业结构升级。该指标能在一定程度上反映整个产业的内部调整结果,并反映整个产业结构本身的优化。
技术进步:本文以全要素生产率的变化衡量技术进步。为了对这一指数进行测算本文,本研究采用了DEA-Malmquist方法[7],这一方法的优势在于可以同时避免方程偏差和规格误差问题。所有计算工作均基于2006~2017年的指标数据库和DEAP 2.1。本文设定的投入项包括资本投入、能源投入和劳动力投入。具体而言,本文使用固定资本存量作为资本输入,前者是根据2006年的价格水平和永续盘存法计算得出的;将地级市消耗的各种能源转换为标准煤,并以此作为能源输入;将从业人员的规模作为劳动输入。最后,本文使用经2006年价格指数平减而得的GDP表征产出。
-
经济发展水平:经济发展水平是影响空气质量的重要因素[8]。本文使用人均GDP来衡量经济发展水平。为了避免严重的多重共线性的影响,本文仅考虑人均GDP的一次项并通过估计系数的正负性判断长三角城市群所处的经济发展阶段。
城市化水平:城市化进程改变了原始的自然和社会条件,城市成为PM2.5污染的空间容器。现有研究已经证实了城市化水平对PM2.5污染扩散的推动作用[9]。本文使用城市人口比例表征城市化水平。
交通密度:交通系统是PM2.5形成的重要来源[10]。近年来,长三角城市群的交通拥堵状况趋于严重,机动车尾气成为加剧PM2.5污染的重要因素。考虑到数据的可用性,本文使用公路长度与城市土地面积之比来衡量交通密度。
温度:TIE et al [11]分析了气候因素对PM2.5污染的影响,发现一定程度的升温会使PM2.5污染状况恶化,战杨志豪等[12]的研究结果也支持这一观点。本文使用地区年平均温度来衡量温度这一变量。
降水:已有研究证明大气降水的沉淀作用是去除细颗粒污染物的重要方法[13]。本文使用地区年降水量来衡量降水。
-
本研究用于分析的PM2.5数据是达尔豪斯大学大气成分分析小组提供的免费公共产品。经济、人口和能源数据来自《中国城市统计年鉴(2008—2018)》、各城市发布的统计公报和其他公开数据。温度和降水数据是从各个城市设置的气象监测站获得的。个别缺失数据通过插补法处理。变量的描述性统计,见表1。
数据的主要处理过程如下:首先搜集长三角城市群26市2007~2017年间,PM2.5污染程度、第三产业产比等指标的数据构成平稳面板数据。其次为了避免伪回归,确保估计结果的有效性,对各面板序列进行了面板单位根检验。在单位根检验的基础上,对模型进行了协整检验和修正。最后通过Hausman检验确定了模型应采用随机效应模型。对于计量分析而言,多重共线性是难以避免的,它会增大回归系数的方差并最终降低模型估计的可信度和效度。在进行正式回归之前,本文基于最小二乘估计对解释变量组进行了多重共线性测试。结果表明,所有变量的VIF均不高于5,这表明解释变量间不存在严重的多重共线性。
-
2007~2017年长三角城市群PM2.5浓度的发展状况,见图1。
图1可知,研究期内,长三角城市群PM2.5污染状况有轻微恶化,PM2.5平均浓度由2007年的53.19 μg/m3略微上升到53.66 μg/m3。从分布状况来看,长三角城市群的北部是PM2.5浓度高值区,尤其是泰州、扬州和盐城等城市。以宁波、台州和舟山等城市所在的东南地区是长三角城市群PM2.5浓度的低值区。高值区和低值区之间的城市连结形成污染中值区。总体来看,2007~2017年间,长三角城市群的PM2.5污染状况保持稳定,略有增加,空间上呈现出由南向北递增的趋势。
本研究认为,2007~2017年间长三角城市群PM2.5呈现稳中略增,形成北多南少分布特征的主要原因在于以下两个方面:(1)尽管长三角城市群各级政府的环保意识在逐渐加强,但生产活动的频繁、产业结构的不合理、生产技术的落后、工业化和城镇化的快速发展等因素使得环境污染的推力和抑制力之间形成了一种平衡的博弈,导致了2007~2017年间,空气污染物排放水平保持基本稳定;(2)经济发展水平会对空气污染物的排放程度带来显著影响。PM2.5的空间分异特征基本与经济发展水平的空间分异特征一致。
-
研究区PM2.5浓度的Moran’s I和Z统计量结果,见表2。
各年份的Moran’s I均﹥0.30且Z统计量显著为正,表明研究区PM2.5浓度具有显著的空间相关性和聚集性。2007~2017年间Moran’s I有所上升,这表明PM2.5浓度在市一级的聚集性有所增强。
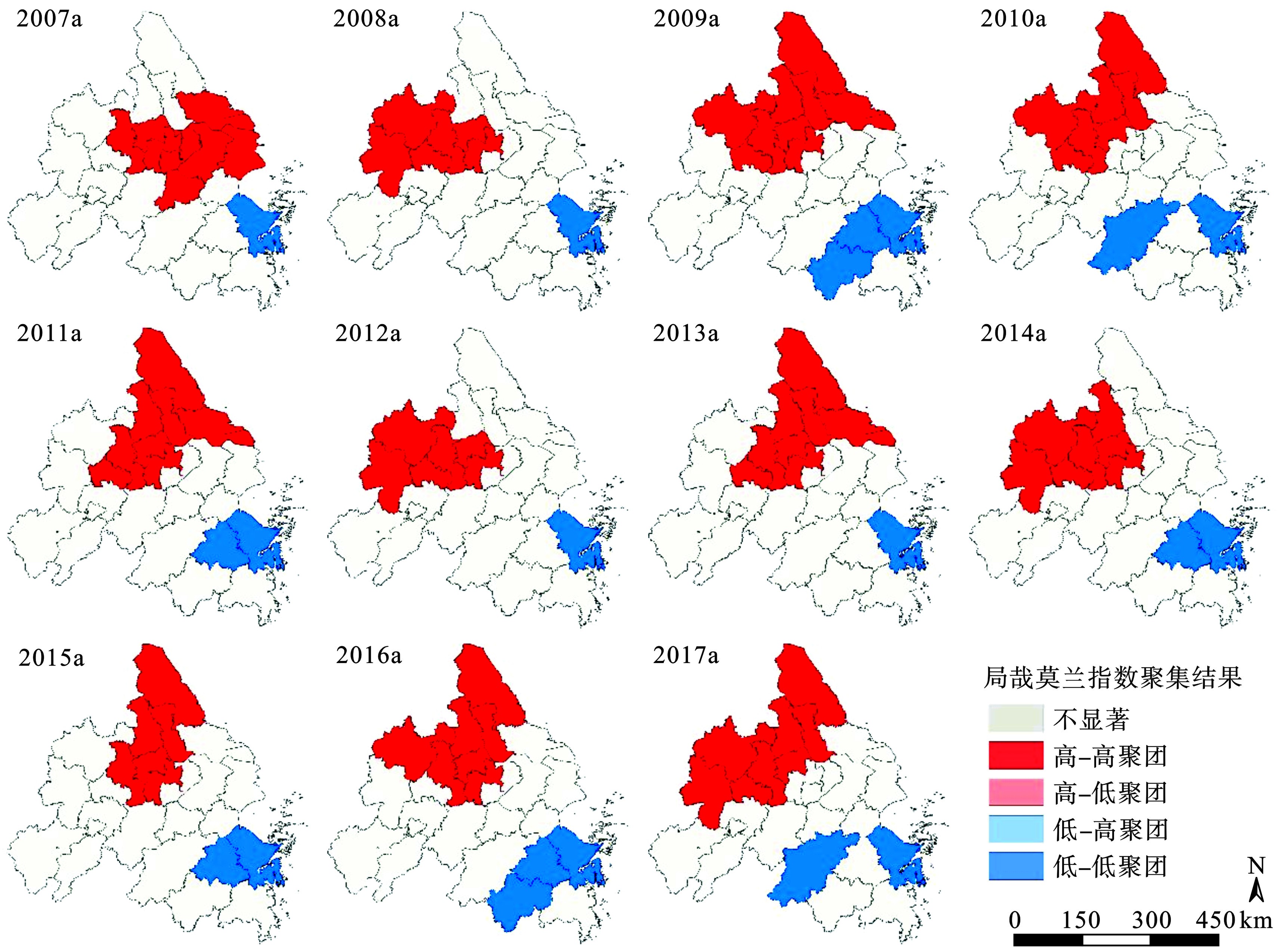
为进一步明晰长三角城市群PM2.5污染的局部空间关联特征,基于ArcGIS 10.5,本文绘制了LISA集聚图,见图2。
LISA集聚图展示的信息与研究区内PM2.5污染的动态高度吻合。高-高聚团和低-低聚团分别集中在研究区的北部和东南部,高-低聚团和低-高聚团较少。由此可见,长三角城市群PM2.5浓度空间聚类类型的分布基本上是稳定的,表明PM2.5污染分布是路径依赖的或是空间锁定的。高-高聚团主要分布在盐城、扬州、南通和滁州等北部城市,低-低聚团主要分布在杭州、宁波和绍兴等南部城市。这一结论进一步论证了长三角城市群PM2.5存在显著的空间分异性,由南向北逐渐加重的结论。
-
基于以上对长三角城市群PM2.5浓度动态演变的和空间相关的可视化分析,可以发现研究区PM2.5浓度具有显著的动态性和空间关联性。因此,相较于ODP模型和SSP模型,DSP模型具有理论上的有效性。为了验证DSP模型的有效性能否在实践中得到延续,本文基于Stata 15软件对3种模型进行依次估计并比较结果。
在DSP模型中,被解释变量的滞后项被作为解释变量且模型具有横截面相依性。因而,使用一般的静态面板模型进行模型测算时必将导致估计参数有偏。为了得到一致的估计量,相关研究广泛采用的估计方法是ARELLANO et al [14]提出的差分广义矩估计。值得注意的是, 当被解释对象的稳态水平调整速度很慢时,该种估计方法将趋于低效。BLUNDELL et al [15]基于差分广义矩估计改进而成的系统广义矩估计很好地解决了上述问题。本研究采用系统广义矩估计对ODP模型进行回归。KUKENOV et al [16]在研究动态面板模型的空间效应时对众多估计方法进行比较,发现系统广义矩估计法的测算效果最好并开发出空间系统广义矩估计。基于此,本文采用空间系统广义矩估计DSP模型。最后,对于SSP模型,本文采用ML方法进行估计[17]。最后,对于SSP模型,本文采用ML方法进行估计[18]。至此,本文分别为3个非常规面板模型制定了具体的估计方法。除此之外,本文还设置了2种不同的估计规范以实现同种模型估计结果的组内比较。具体而言,模型(a)、模型(c)和模型(e)是仅考虑了产业和技术对PM2.5浓度独立效应的简洁模型,模型(b)、模型(d)和模型(f)是考虑了以上两者交互效应的完整模型。
为了判断系统广义矩估计方法是否被正确指定,有必要进行2组规格测试。第一,应使用过度识别检验判断工具变量的整体有效性。本文报告了Hansen统计量。检验值均﹥0.10,没有拒绝原假设,这表明不存在过度约束问题。第二,系统广义矩法需满足估计量一致这一使用条件,即误差项不存在序列相关,对此本文使用AR测试进行残差项的序列相关性检验。AR(1)检验和AR(2)检验的结果表明随机扰动项具有一阶序列相关且没有二阶序列相关,满足矩约束条件要求。对空间杜宾模型、空间滞后模型和空间误差模型进行合理的筛选是估计空间面板模型的关键步骤。对于SSP模型和DSP模型,本文首先基于混合回归构建拉格朗日乘子(LM)和稳健性拉格朗日乘子(Robust LM)统计量进行空间自相关性检验。LM–Lag和Robust LM–Lag均通过了5%水平的显著性检验,LM–Error和Robust LM–Error均未通过10%水平的显著性检验。因此,本文的模型(c)~(f)均使用空间滞后模型(SLM)模型进行估计。3种模型的具体估计结果,见表3。
基于表3,比较ODP模型和DSP模型中的PM2.5污染的一阶滞后系数,可以发现DSP模型的系数小于ODP模型的系数。这意味着在考虑地理距离和空间溢出效应时,DSP模型可以部分纠正ODP模型的误差,从而使估算更加准确和可靠。同时,这一结果表明在考虑前期因素和动态效应时,由于可以将先前因素对当前PM2.5污染的影响与当前因素的影响剥离,DSP模型可以部分纠正SSP模型的误差,使得估算更加准确可靠。更直观的是,在选择的变量均具有理论支持的前提下,模型(e)和(f)中变量的估计系数比模型(a)~(d)所对应的系数更加显著。总之,DSP模型在理论和实践上都较其他模型显示出其独有的优势。因此,本文选用DSP模型作为最终解释模型。
-
根据表3中模型(e)和模型(f)所示结果,可以得到以下结论。
(1)产业结构的升级有利于降低PM2.5污染。产业结构升级在简洁模型和完整模型中的系数为分别−0.132 4和−0.149 8,且均显著。产业结构的升级即第一产业和第二产业比重的降低、第三产业比重的提高。一方面,第二产业以制造业和建筑业为主,是空气污染物的最主要来源。第三产业以服务业为主,其空气污染物排放水平远低于第二产业。因此,产业结构升级通过降低污染源的比重有效减少了PM2.5污染强度。另一方面,产业结构升级还促进了产业之间能源要素的合理配置和有效利用,通过促进劳动生产率和能源利用效率的提高来帮助协调产业之间的发展,这有效地降低了PM2.5污染。
(2)技术进步能够降低PM2.5污染程度。完整模型中,技术进步的估计系数在1%的显著性水平上显著为负,系数为−1.427 7。这表明,技术进步可以降低长三角城市群的PM2.5污染程度。技术进步可以显著降低环境污染水平的原因在于,一方面,技术进步能够显著提升生产效率和能源利用效率。生产效率和能源利用效率的提升能够降低单位产值的能源消费量,从而降低污染物排放水平。另一方面,技术进步能够提升废气处理和二次利用水平,对污染物排放水平的降低具有直接影响。
(3)产业结构升级和技术水平提高的综合效应会对PM2.5的排放产生明显的抑制作用。技术和产业因素交互项的估计系数为负且显著,系数为−0.393 1。表明技术进步和产业结构升级的联合作用对PM2.5污染的缓解作用也是显著的。技术进步可以帮助企业改造、升级和更新其设备,促进技术密集型产业的发展;可以加速经济发展由粗放型向集约型转变,进而促进产业结构升级。通过对产业结构升级和技术进步的系数比较,可以发现,在提高长三角城市群空气质量的过程中,尽管产业和技术变动均有一定的积极作用,但技术进步的作用更大。
(4)对于控制变量,经济发展水平对PM2.5污染有显著的抑制作用。相对于大陆其他地区,长三角城市群总体上已跨过经济发展初期,经济增长带来的规模效应缓解了城市PM2.5污染。城市化水平的系数为正值但并不显著,表明城市化可以在一定程度上加剧长三角城市群的空气污染。城市化进程要求政府建设大量基础设施、住宅楼及相关设施。城市人均能源消耗较高,因此,城市化可能会增加PM2.5污染强度。其次,在城市化进程中,污染物的处理不是集中的,污染物的处理过程既不能实现规模经济,也不能实现循环经济。污染物处理设施不足和分配效率低会导致污染物处理率低和回收率低,从而导致大量的细颗粒污染物排放。交通密度也是PM2.5污染的驱动因素,主要是因为路网密度的增加将使单位土地面积的机动车数量成倍增加。机动车数量的增加不仅会导致燃料消耗增加,还会使道路拥堵倍增,这不利于机动车所用燃料的高效燃烧。对于自然因素,与现有研究所呈现的结果一致,高温使城市更易形成稳定的温层,从而导致PM2.5颗粒稳定且大量悬浮在空气中。降水过程的沉淀作用可以促进气溶胶的湿沉降从而实现对PM2.5颗粒的冲刷。
-
本研究分析了长三角城市群的产业结构升级和技术进步对PM2.5污染的影响。结果表明,长三角城市群的PM2.5污染存在显著的时序动态演变特征和空间相关性。因此,对于研究区而言,减少细颗粒物污染的政策应着重于加大力度和区域联合防控。使用动态空间面板模型进行的进一步分析表明,产业结构升级和技术进步对PM2.5污染的影响存在显著差异。具体而言,尽管产业结构变动产生的效果很重要,但技术进步在缓解PM2.5污染的过程中发挥着更大的作用。此外,技术进步和产业结构升级的联合效应对PM2.5污染具有抑制作用。基于此,提出建议如下。
(1)根据PM2.5时空演变格局分析及Moran’ I测算的结果,长三角城市群不同地区有不同的PM2.5排放水平。因此,从空间视角来看,长三角城市群需要分类施策,根据当地情况和经济发展水平,实施不同的区域颗粒污染物减排战略。根据空气污染程度和空间相关性,长三角城市群被分为高污染区、中污染区和低污染区3种类型。具体来说,盐城、扬州、泰州、南通、滁州、合肥和马鞍山属于高污染区,湖州、嘉兴、杭州、绍兴、宁波、金华和台州属于低污染区,其余城市属于中污染区。对于PM2.5高污染区,政府应重点关注重工业造成的污染,严格控制与生产有关的污染并减少机动车数量。中污染区可以被视为空气污染措施施行的次要重点地区。对于这些地区,政府应加强空气污染的预防和治理,并严格控制燃煤总量。低污染区可以被视为未来需要采取空气污染措施的区域。对于该类型地区,政府都需要加强对固定污染源和移动污染源的补救,并加快向清洁生产的转化。
(2)由于长三角城市群PM2.5污染状况存在显著的空间差异,且长三角城市群包含了4个省级行政区(上海、江苏、浙江和合肥)和26个地级市,不同行政区域之间的区域合作是治理空气污染的关键。长三角城市群应建立区域联合防控机制,积极推动颗粒污染物减排的区域合作。一方面,政府应明确监督空气污染的主要机构的职责,制定统一的标准、法律和政策体系,协调区域环境管理,建立区域内的污染补偿和利益协调机制。另一方面,应建立区域环境信息共享网络,发挥联合预警效应和示范效应。此外,应进一步强化环境管理的集中化,扩大政府在环境保护事务中的管理范围。除此之外,应加快对地方政府评估体系的更新,推行多元化和针对绿色产业的评估体系,继续在绩效评估中强调环境保护和环境质量。
(3)根据动态空间面板模型回归的结果,产业结构升级和技术水平提升会显著降低PM2.5的排放水平。长三角城市群应优化绿色产业结构和能源结构的设计,并促进其不断升级。一方面,提升绿色生产技术,淘汰落后工艺。应提高制造企业的环境标准、环境法规和污染物排放要求,限制能源密集型和污染物密集型制造业的快速增长,逐步淘汰落后的生产方式,解决产能过剩的矛盾。另一方面,应以发展循环经济为导向提升产业结构,鼓励低排放环保产业,积极推动环保制造业的发展。防止资源浪费和过度开发,通过自主研究和技术引进不断提高设备技术水平。除此之外,政府还应增加第二产业中可再生能源和新能源类型的比重。
长三角城市群PM2.5污染时空特征及其优化路径
——基于产业转型和技术升级的视角Spatio-temporal characteristics and optimal path of PM2.5 pollution in Yangtze River Delta urban agglomeration
-
摘要: 准确把握PM2.5污染的时空特征及其驱动效应,有助于推动长三角城市群实现良性、可持续发展。基于2007~2017年的市级面板数据集,文章使用动态空间面板(DSP)模型对长三角城市群PM2.5污染的时空特征及其产业和技术的驱动效应进行了实证分析。结果表明:地区PM2.5污染存在显著的时序动态演变特征和空间相关性,区域内部PM2.5污染的空间异质性分布较为稳定;尽管产业结构升级和技术进步均有利于缓解PM2.5污染,但技术进步发挥了更重要的作用;产业结构升级和技术进步的联合效应可以显著抑制PM2.5污染。为持续提高长三角城市群的空气质量,应建立区域差异化的治理和联合防控机制。地区政府应促进产业结构和能源结构不断升级,通过自主开发和技术引进的手段发挥技术进步对环境治理的积极效应。Abstract: Accurately grasping the spatio-temporal characteristics of PM2.5 pollution and its driving effect will help to promote the sustainable development of the Yangtze River Delta urban agglomeration. Based on the city-level panel data set from 2007 to 2017, this paper uses a dynamic spatial panel (DSP) model to analyze the distribution and driving factors of PM2.5 pollution in the Yangtze River Delta urban agglomeration. The results show that there are significant temporal dynamic evolution characteristics and spatial correlation of PM2.5 pollution in the region, and the spatial heterogeneity distribution of PM2.5 pollution within the region is relatively stable. For the Yangtze River Delta urban agglomeration, although the industrial structure upgrading and technological progress are conducive to alleviating PM2.5 pollution, technological progress has played a more important role. In addition, another important finding is that the combined effect of industrial structure upgrading and technological progress can significantly suppress PM2.5 pollution. To continuously improve the air quality of the Yangtze River Delta urban agglomeration, a regionally differentiated governance and joint prevention and control mechanism should be established. Regional governments should promote the continuous upgrading of industrial structure and energy structure, and exert the positive effects of technological progress on the environmental governance through the independent development and technology importing.
-
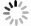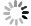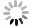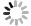
-
表 1 变量的统计性描述
Table 1. Statistical description of variables
指标 PM2.5污染/mg·m−3 产业结构升级/% 技术进步 经济发展/元 城市化水平/% 交通密度/km·km−2 温度/℃ 降水/mm 平均值 50.34 41.76 1.04 65 530.06 53.27 1.41 16.93 1 323.41 标准差 10.17 8.18 0.38 31 673.25 17.14 0.38 1.01 350.28 极小值 23.03 23.36 0.81 10 588.99 17.90 0.81 13.80 605.20 极大值 71.24 71.80 2.65 154 983.70 89.39 2.65 19.30 2 626.80 表 2 长三角城市群PM2.5的全局Moran’s I结果
Table 2. Global Moran's I results of PM2.5 in the Yangtze River Delta urban agglomerations
t/a 全局Moran’s I Z 2007 0.395*** 3.195 2008 0.472*** 3.759 2009 0.450*** 3.598 2010 0.519*** 4.044 2011 0.522*** 4.153 2012 0.329*** 2.786 2013 0.453*** 3.608 2014 0.634*** 4.909 2015 0.534*** 4.222 2016 0.476*** 3.762 2017 0.507*** 3.979 注:***表示p<0.01。 表 3 3组模型的回归结果
Table 3. The regression results of three groups of models
系数 ODP模型 SSP模型 DSP模型 模型(a) 模型(b) 模型(c) 模型(d) 模型(e) 模型(f) τ 0.479 9*** 0.414 1*** − − 0.265 5*** 0.262 2*** −3.33 −2.86 − − −4.24 −4.65 ρ − − 0.658 6*** 0.645 9*** 0.609 3*** 0.602 8*** − − −18.92 −16.87 −14.89 −13.93 ln Is 0.505 6 0.713 9 −0.145 6*** −0.166 4*** −0.132 4** −0.149 8*** −1.41 −1.37 (−2.58) (−2.86) (−2.59) (−2.77) ln Tp −0.190 1 −10.150 6 −0.026 3 −1.800 3*** −0.014 2 −1.427 7*** (−1.10) (−1.37) (−0.53) (−2.74) (−0.35) (−2.65) ln(Is × Tp) − −2.809 1 − −0.491 6*** − −0.393 1*** − (−1.39) − (−2.63) − (−2.57) ln Ed −0.061 0 −0.091 6 −0.146 2** −0.145 5** −0.099 5* −0.103 5** (−0.71) (−0.94) (−2.34) (−2.44) (−1.75) (−1.94) ln Ul 0.556 2*** 0.563 5*** 0.009 5 0.036 0 0.067 4 0.077 4 −3.08 −2.79 −0.07 −0.25 −0.49 −0.59 ln Tr 0.381 2 0.391 6 0.036 5 0.028 6 0.036 1 0.031 7 −1.51 −1.02 −1.17 −0.87 −0.94 −0.77 ln Te −0.522 5* −0.422 8 1.053 4*** 0.999 3*** 0.874 3*** 0.836 4*** (−1.66) (−1.01) −3.36 −3.17 −3.21 −3.06 ln Pr 0.379 5*** 0.368 5*** −0.070 0* −0.071 6* −0.068 4* −0.069 8** −4.08 −3.91 (−1.79) (−1.85) (−1.83) (−1.87) 观测值 260 260 286 286 260 260 LM–Error检验 − − −0.131 −0.13 −0.128 −0.125 Robust LM–Error检验 − − −0.146 −0.149 −0.142 −0.146 LM–Lag检验 − − −0.018 −0.016 −0.009 −0.008 Robust LM–Lag检验 − − −0.037 −0.028 −0.016 −0.011 AR(1)检验 0 0 − − 0 0 AR(2)检验 −0.418 −0.916 − − −0.48 −0.355 Hansen过度识别检验 −0.183 −0.188 − − −0.222 −0.22 注:*、**和***分别表示p<0.10、p<0.05和p<0.01;括号内为Z值。 -
[1] 姜磊, 周海峰, 赖志柱, 等. 中国城市PM2.5时空动态变化特征分析: 2015—2017年[J]. 环境科学学报, 2018, 38(10): 3816 − 3825. [2] GENIAUX G, MARTINETTI D. A new method for dealing simultaneously with spatial autocorrelation and spatial heterogeneity in regression models[J]. Regional Science and Urban Economics, 2018, 72: 74 − 85. doi: 10.1016/j.regsciurbeco.2017.04.001 [3] CHEN J, ZHOU C S, WANG S J. Identifying the socioeconomic determinants of population exposure to particulate matter (PM2.5) in China using geographically weighted regression modeling[J]. Environmental Pollution, 2018, 241: 494 − 503. doi: 10.1016/j.envpol.2018.05.083 [4] ROMANO C L, TRAÙ F. The nature of industrial development and the speed of structural change[J]. Structural Change and Economic Dynamics, 2017, 42: 26 − 37. doi: 10.1016/j.strueco.2017.05.003 [5] 沈冰, 李鑫. 金融发展、产业结构升级与能源效率提升[J]. 经济问题探索, 2020(12): 131 − 138. [6] 王敏, 李亚非, 马树才. 智慧城市建设是否促进了产业结构升级[J]. 财经科学, 2020(12): 56 − 71. doi: 10.3969/j.issn.1000-8306.2020.12.006 [7] CHENG Z, LI L, LIU J. Industrial structure, technical progress and carbon intensity in China’s provinces[J]. Renewable and Sustainable Energy Reviews, 2018, 81: 2935 − 2946. doi: 10.1016/j.rser.2017.06.103 [8] 徐娜娜. 基于DEA-Malmquist指数开放型经济下河南省三次产业全要素生产率测算[J]. 数学的实践与认识, 2020, 50(18): 303 − 309. [9] 梁睿, 高明, 吴雪萍. 环境规制与大气污染减排关系的进一步检验——基于经济增长的门槛效应分析[J]. 生态经济, 2020, 36(9): 182 − 187. [10] 郭一鸣, 蔺雪芹, 边宇. 中国城市群空气质量时空演化特征及其影响因素[J]. 生态经济, 2019, 35(11): 167 − 175. [11] 张晓春, 丘建栋, 屈新明, 等. 深圳市交通排放污染物浓度特征与影响因素[J]. 深圳大学学报(理工版), 2020, 37(2): 178 − 186. [12] TIE X, LONG X, DAI W. Surface atmospheric PM2.5 optical, satellite distribution depth and of related effects on crop production in China[J]. Air Pollution in Eastern Asia, 2017, 16: 479. [13] 战杨志豪, 谢旻, 罗干, 等. 2018年冬季南京重霾污染特征及气象因素分析[J]. 环境科学学报, 2020, 40(11): 4038 − 4047. doi: 10.13671/j.hjkxxb.2020.0210 [14] JIN J Q, DU Y, XU L J. Using Bayesian spatio-temporal model to determine the socio-economic and meteorological factors influencing ambient PM2.5 levels in 109 Chinese cities[J]. Environmental Pollution, 2019, 254: 113023. doi: 10.1016/j.envpol.2019.113023 [15] ARELLANO M, BOND S. Some tests of specification for panel data: Monte carlo evidence and an application to employment equations[J]. Review of Economic Studies, 1991, 58: 277 − 297. doi: 10.2307/2297968 [16] BLUNDELL R, BOND S. Initial conditions and moment restrictions in dynamic panel data models[J]. Journal of Econometrics, 1998, 87: 115 − 143. doi: 10.1016/S0304-4076(98)00009-8 [17] KUKENOVA M, MONTEIRO J. Spatial Dynamic Panel Model and System GMM: A Monte Carlo investigation. 2009 [R]. IRENE Working Papers 09-01, Irene Institute of Economic Research. [18] ELHORST J P. Specification and estimation of spatial panel data models[J]. International Regional Science Review, 2003, 26: 244 − 268. doi: 10.1177/0160017603253791 -



 下载:
下载: