-
袋式除尘器具有除尘效率高、处理风量范围广、可回收有价值颗粒等优点,被广泛应用于除尘领域。为在现场条件有限的情况下使袋式除尘器达到超低排放标准[1-3],相关研究者多采取改造的方式提升其性能。其中,将传统除尘器应用的圆筒滤袋改为褶皱滤袋能在不增加除尘器体积的基础上增加过滤面积,已成为除尘器改造的重要选择[1]。在圆筒滤袋改造为褶皱滤袋的工程实践中,通常除尘器本体不变,但滤袋长度会发生变化,进而带来除尘器内部流场的变化。长滤袋过滤面积大,有利于过滤效率的提升。然而,滤袋变短可增加粉尘沉降的空间,也有利于提高除尘器的效率。因此,有必要对不同袋长除尘器内部气流和粉尘的运动进行研究,以进一步明确袋长对除尘器流场及粉尘沉降的影响。
目前,褶皱滤袋已在实践中有一定应用。杜然等[1]改造高炉出铁厂与矿槽除尘器,将长6 m的圆筒滤袋改为长5.5 m的褶皱滤袋。张波波等[2]改造焦炉装煤除尘器,将6 m的圆筒滤袋改为同等长度的褶皱滤袋。赵金怀等[3]改造出铁场袋式除尘器,将6.5 m圆筒滤袋改为6 m褶皱滤袋。孙志钜等[4]改造燃煤锅炉布袋除尘器,将长8 m的圆筒滤袋改为5 m的褶皱滤袋。王锦等[5]改造水泥厂除尘器,将3 m圆筒滤袋改为2 m滤筒。在以上改造案例中,改造褶皱滤袋不仅实现了稳定超低排放达标,同时降低了运行压差。然而,改造过程中滤袋的长短选择不一,尚存在由于滤筒长度大大缩减会在除尘器下方给粉尘带来自由沉降空间,以至于过滤负荷降低的问题。该问题并未得到很好解决。
随着计算流体力学的发展,数值模拟方法因其直观、高效的特点,被应用于袋式除尘器流场及褶皱形式 [6-7]的研究。在除尘器流场研究方面,刘含笑等[8]创建滤袋长9 m的单条滤袋模型,研究数值模拟边界条件对滤袋速度和压力计算结果的影响。黄冶文[9]创建滤袋长10 m的除尘器模型,研究得出滤袋长度是影响气流上升速度的关键因素。该研究建立的除尘器模型中滤袋数量较少,并未改变除尘器的滤袋长度。SANGCHEL等 [10] 建立袋长3、10、12、15 m单条滤袋除尘器模型,研究滤袋表面的过滤速度分布时发现,随着滤袋长度的增加,过滤速度变得不均匀,滤袋顶部过滤速度更高。THOMAS等[11]建立袋长3 m滤袋数49条的除尘器模型,研究不同进风口位置对除尘器流场影响。毛锐等[12]利用数值模拟对除尘器内流场进行模拟,证明增加导流板可使内部流场更加均匀。丁倩倩等[13]采用 CFD 模拟 6、8和10 m 3种袋长除尘器内的三维流动,发现相同过滤速度下10 m的长滤袋除尘器内部的速度分布比较均匀。但研究在改变滤袋长度的同时也改变了除尘器箱体长度。方璨等[14]在保持除尘器箱体尺寸不变的条件下针对袋长2、3、3.5 m,装有3条褶皱滤袋的除尘器进行了分析,确定袋长3 m的滤袋室内流场分布更均匀。
褶皱滤袋改造技术是在除尘器本体不变的基础上进行的,需要在保持除尘器内部空间不变的前提下分析袋长对流场的影响。目前,对实际工程中不改变袋除尘器外部箱体的情况下,袋长对流场影响的研究还比较少。基于此,本研究在不改变大型袋式除尘器本体条件下,利用数值模拟方法,对袋长L=3、4、5、6 m的除尘器进行流场与粉尘沉降的研究。探究袋式除尘器中圆筒滤袋改为褶皱滤袋后,滤袋长度变化对除尘器内部流场及粉尘在灰斗中沉降的影响。以期为下进风袋式除尘器袋长设计及袋式除尘器的改造提供参考。
-
袋式除尘器内部流场可视为不可压缩、湍流、等温和稳定流场。控制方程包括质量守恒和动量守恒方程。湍流模型则选用标准Realizable k-
$ \varepsilon $ 双方程模型[15-16]。粉尘在除尘器内运动的模拟采用离散相模型(discrete phase model,DPM),粉尘颗粒运动过程的受力平衡方程为[17]式(1)。式中:
$ \overrightarrow{u} $ 为气体的速度,m·s−1;$ {\overrightarrow{u}}_{\mathrm{p}} $ 为粉尘颗粒的速度,m·s−1;$ \rho $ 为气体密度,kg·m−3;$ {\rho }_{\mathrm{p}} $ 为粉尘颗粒的密度,kg·m−3;$ \overrightarrow{F} $ 为附加力包括布朗力、Saffman升力和热泳力,N·kg−1。本研究考虑粉尘颗粒主要受重力、浮力和气流阻力的作用,故附加力可忽略。其中,$ {\tau }_{\mathrm{r}} $ 为颗粒的弛豫时间,计算式为式(2)。式中:
$ \mu $ 为连续相的分子黏度;$ {d}_{\mathrm{p}} $ 为粉尘颗粒直径,m;Cd为气动阻力系数。其中,Re为颗粒雷诺数,计算公式见式(3)。滤袋为多孔介质,故选取多孔阶跃模型进行模拟,并设置为多孔阶跃边界,计算渗透率方法符合达西公式(式(4))。
式中:
$ \Delta P $ 为压力损失,Pa;$ \mu $ 为流体动力粘性系数,Pa·s;$ \alpha $ 为渗透率,m2;$ v $ 为垂直于过滤介质表面的速度分量,m·s−1;C2为压力跃升系数,本研究中C2=0;$ \Delta m $ 为过滤介质的厚度,m。 -
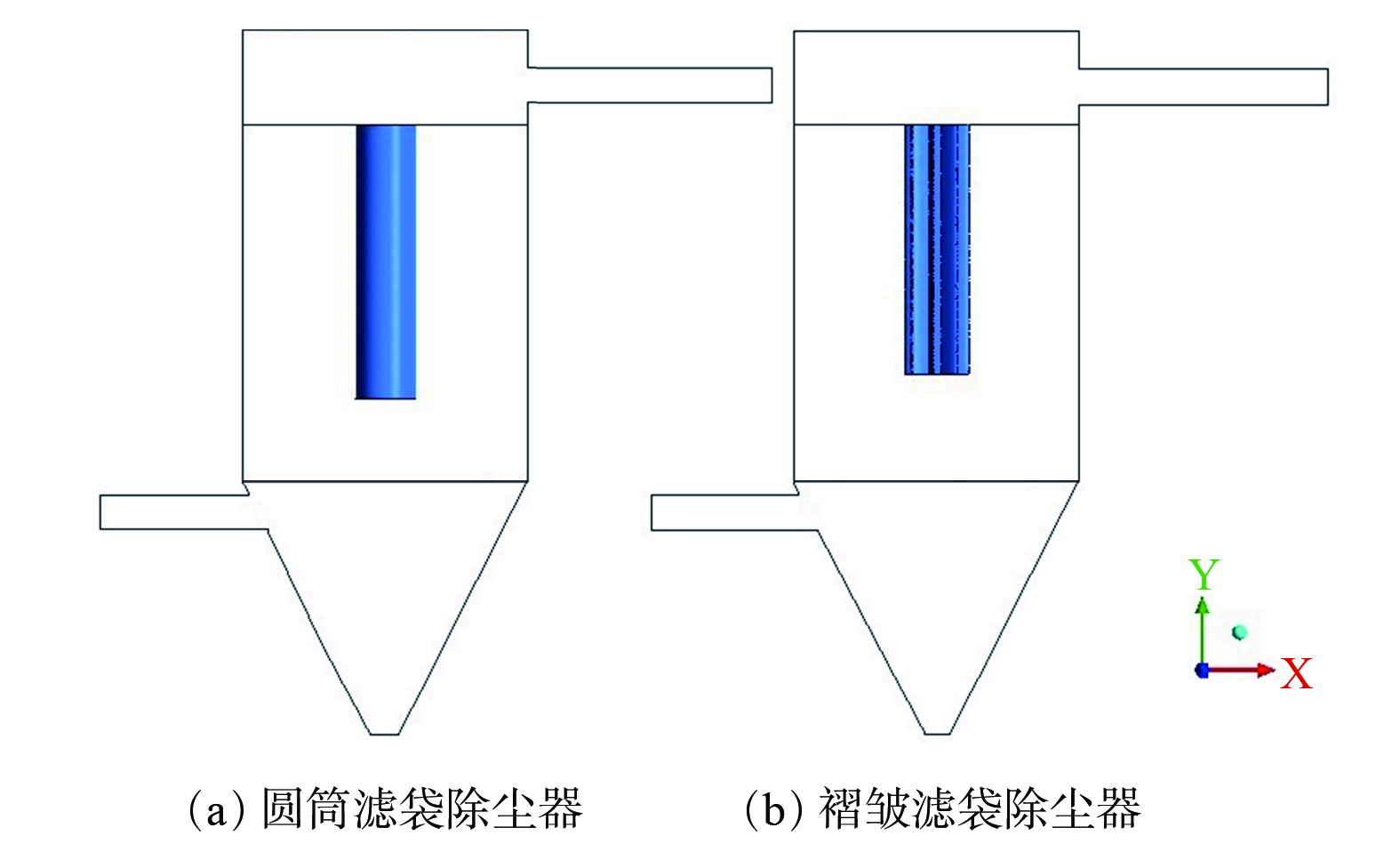
1)几何模型。参考下进风式袋式除尘器的实际尺寸建立几何模型。袋式除尘器上箱体长宽高分别为3 080 mm×3 610 mm×550 mm;中箱体长宽高分别为2 480 mm×3 610 mm×6 150 mm;灰斗高2 000 mm;出灰口尺寸为600 mm×600 mm,进口长宽1 240 mm×300 mm;滤袋共150条,按照15排10列布置[16]。因褶皱滤袋结构在划分网格过程中所需网格数量大增,故在模拟中将其简化为等效圆筒形滤袋,直径160 mm长,袋长分别为L=3、4、5、6 m。简化方法的正确性验证见本文第三部分。图1为袋长分别为3 m和6 m时袋式除尘器的几何模型。
2)边界条件和求解器设置。边界条件[11]:除尘器出口处压力出口,−1 000 Pa;除尘器入口速度为14.96 m·s−1;颗粒物入射速度14.96 m·s−1;滤袋为8褶滤袋,外径相等、流量和压力相同,等效为圆筒滤袋,其渗透率为2×e−11 m2,厚度2 mm。因本研究重点分析进入除尘器粉尘的沉降率,即直接沉降在灰斗中的粉尘质量占进入除尘器总质量的百分比,故定义滤袋的离散相边界条件为trap(捕捉)。在其他壁面定义灰斗的边界条件为trap(捕捉),除尘器的其他壁面为reflect(反射)。
求解方法采用SIMPLE算法,对流项离散格式为二阶迎风格式,压力插值格式为Second-Order,采用DPM模型进行粉尘运动模拟。除尘器所处理粉尘的粒径分布参考表1[18]。数值模拟中对粉尘颗粒设置采用Rosin-Rammler分布,粉尘颗粒密度为900 kg·m−3,中位粒径为62 μm。进行粉尘颗粒在除尘器内部运动的非稳态计算时,取计算时间为200 s。前5 s时间步长为0.1 s,5~200 s时间步长为1 s。
-
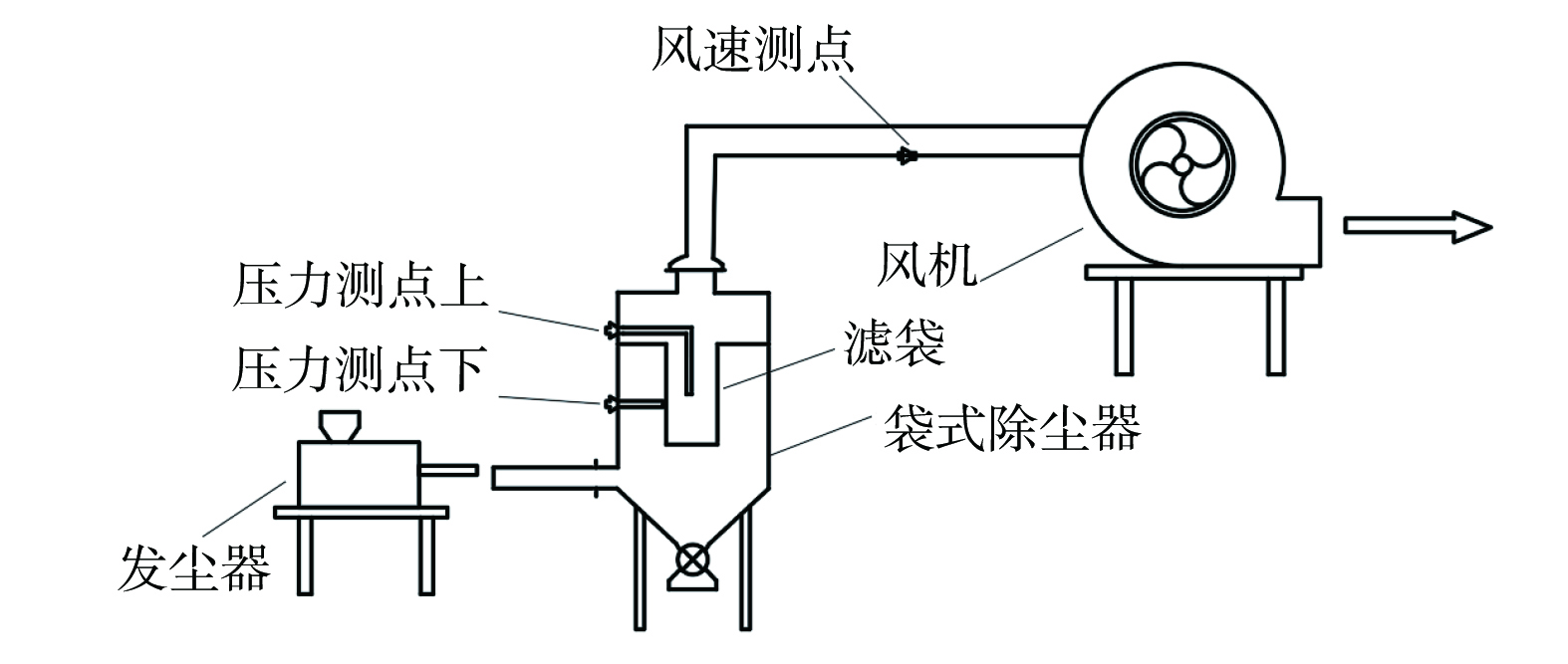
为了解圆筒滤袋与褶皱滤袋的过滤特性,并对模拟方法及将褶皱滤袋等效为圆筒滤袋方法的有效性进行验证,先对圆筒滤袋和褶皱滤袋进行模型实验。图2为实验装置图。实验装置主要包括发尘器、袋式除尘器、管道和风机4个部分。
装置中圆筒滤袋直径为180 mm、长为770 mm、过滤面积为0.411 m2。安装的褶皱滤袋褶数N=8,直径为180 mm、长为700 mm、褶高为50 mm、过滤面积为0.536 m2。圆筒滤袋与褶皱滤袋材料均为涤纶,厚度为2 mm、克重为918 g·m−2。在风速测点位置采用热线风速仪(TESTO425,德国德图公司)对管道风速进行测试,计算得到系统风量,并根据需要通过变频器调整风机转速以改变系统风量。过滤风量条件为0.206~1.233 m3·min−1。利用手持式压力传感器(TESTO512,德国德图公司)在压力测点处测量该风量下洁净圆筒和褶皱滤袋的阻力,根据过滤面积与过滤风量以确定过滤风速,为0.5~3.0 m·min−1。
为确定粉尘进入除尘器后在灰斗中的直接沉降率,在风量1.233 m3·min−1时,对圆筒滤袋与褶皱滤袋进行荷尘实验。在除尘器进风口处利用发尘器加入氧化铝粉尘,粉尘的中位径为40 μm,发尘量为5.8 g·min−1。至滤袋阻力为1 000 Pa时,停止发尘,不进行清灰,测量最终灰斗中粉尘质量。记录发尘时间,并计算总发尘量,通过计算灰斗中粉尘质量与总发尘质量的比,以确定粉尘在灰斗中沉降率。
-
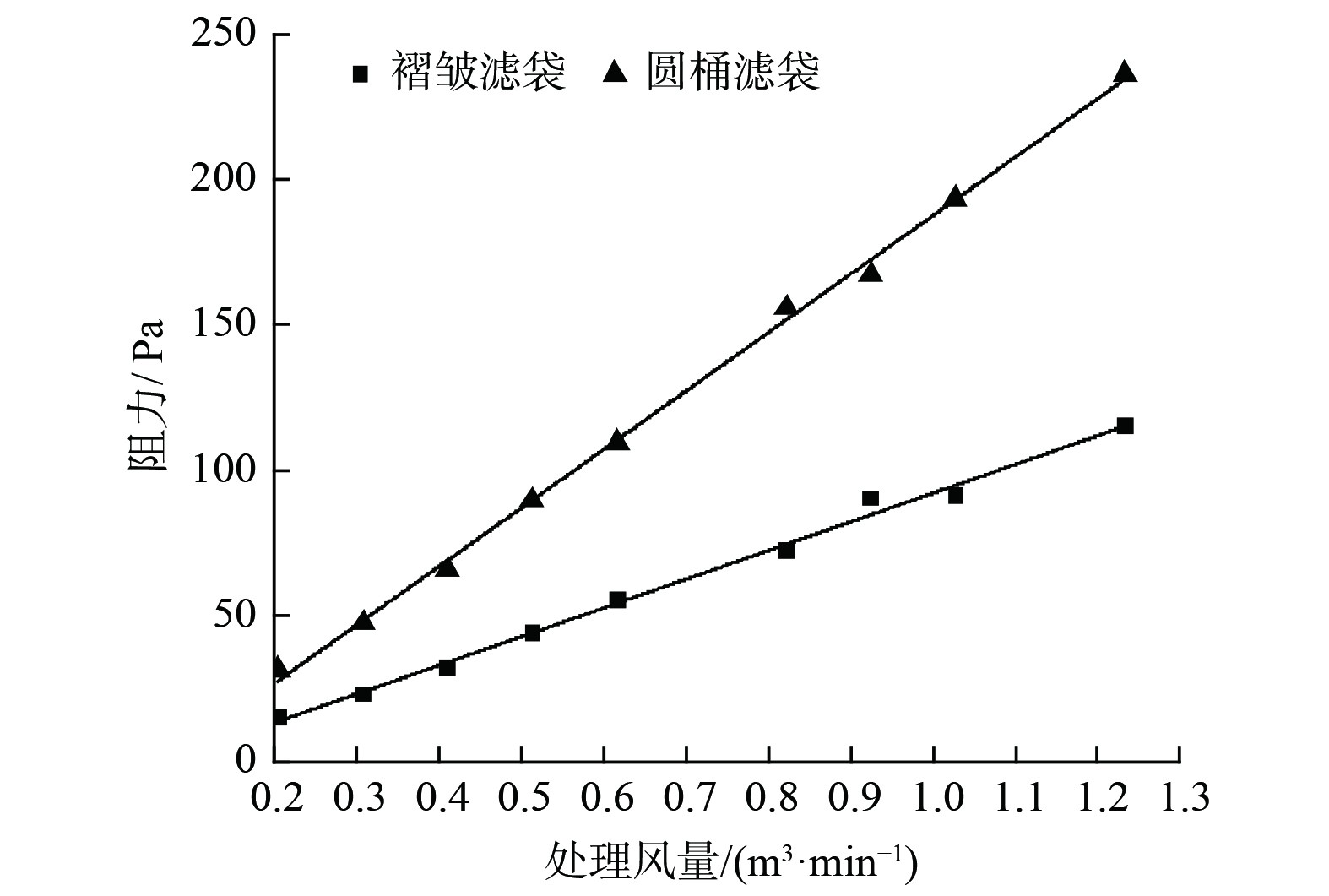
图3为褶皱滤袋与圆筒滤袋在相同处理风量下的压力对比图。在相同过滤风量下,同样材质褶皱滤袋的过滤阻力明显低于同过滤袋的阻力,且处理风量越大,阻力降低值越大。在测试条件下空气动力粘性系数为1.79×10−7Pa·s。基于达西公式,计算得到圆筒滤袋的渗透率为9.08×e−12 m2。
在风量1.233 m3·min−1(对应圆筒滤袋过滤风速为3.0 m·min−1)时,2种滤袋除尘器内部沉降到灰斗中的粉尘分别为总粉尘的73.50%、85.70%。在褶皱滤袋除尘器中,粉尘在灰斗中的沉降率明显增加。
-
1)模拟与实验对比。首先,利用SOLIDWORKS三维建模软件建立实验除尘器的等比例简化模型。图4为实验除尘器几何模型。选取在处理风量为0.411、1.233 m3·min−1的条件下对除尘器进行流场模拟。由图5可知,在不同风量下,圆筒滤袋的压力模拟值分别为70、234 Pa,而实验测得压力值为65、236 Pa,结果非常接近。
由于褶皱滤袋结构较复杂,对大型除尘器进行模拟过程中,按照褶皱结构建模,网格划分量数量太大计算困难,因此,在后续研究中考虑将褶皱滤袋简化为圆筒滤袋进行计算。这里采用流量当量直径法进行简化,即保持两者过滤流量相同,且圆筒滤袋具有与褶皱滤袋相同的外径,用与褶皱滤袋有相同阻力的圆筒滤袋代替褶皱滤袋。根据达西定律,此这时只要计算出圆筒滤袋相应的渗透率,即可实现上述等效。由实验数据可得出褶数N=8褶皱滤袋按上述原则等效为圆筒滤袋后,其滤袋渗透率为1.49×e−11 m2,约为圆筒滤袋的1.6倍。因此,进一步将褶皱滤袋改为相同长度的圆筒滤袋建模,并用等效渗透率进行模拟。在不同风量下,褶皱等效圆筒滤袋除尘器的压力模拟值分别为35、120 Pa,实验测得褶皱滤袋除尘器的压力值分别为32、115.3 Pa。
在处理风量为1.233 m3·min−1的条件下进行粉尘沉降模拟。在圆筒滤袋、褶皱滤袋、褶皱等效圆筒滤袋的除尘器中,粉尘在灰斗中的沉降率分别为74.21%、86.18%与86.92%。模拟结果与实验结果具有良好的一致性。这表明多孔阶跃边界条件、Realizable k-
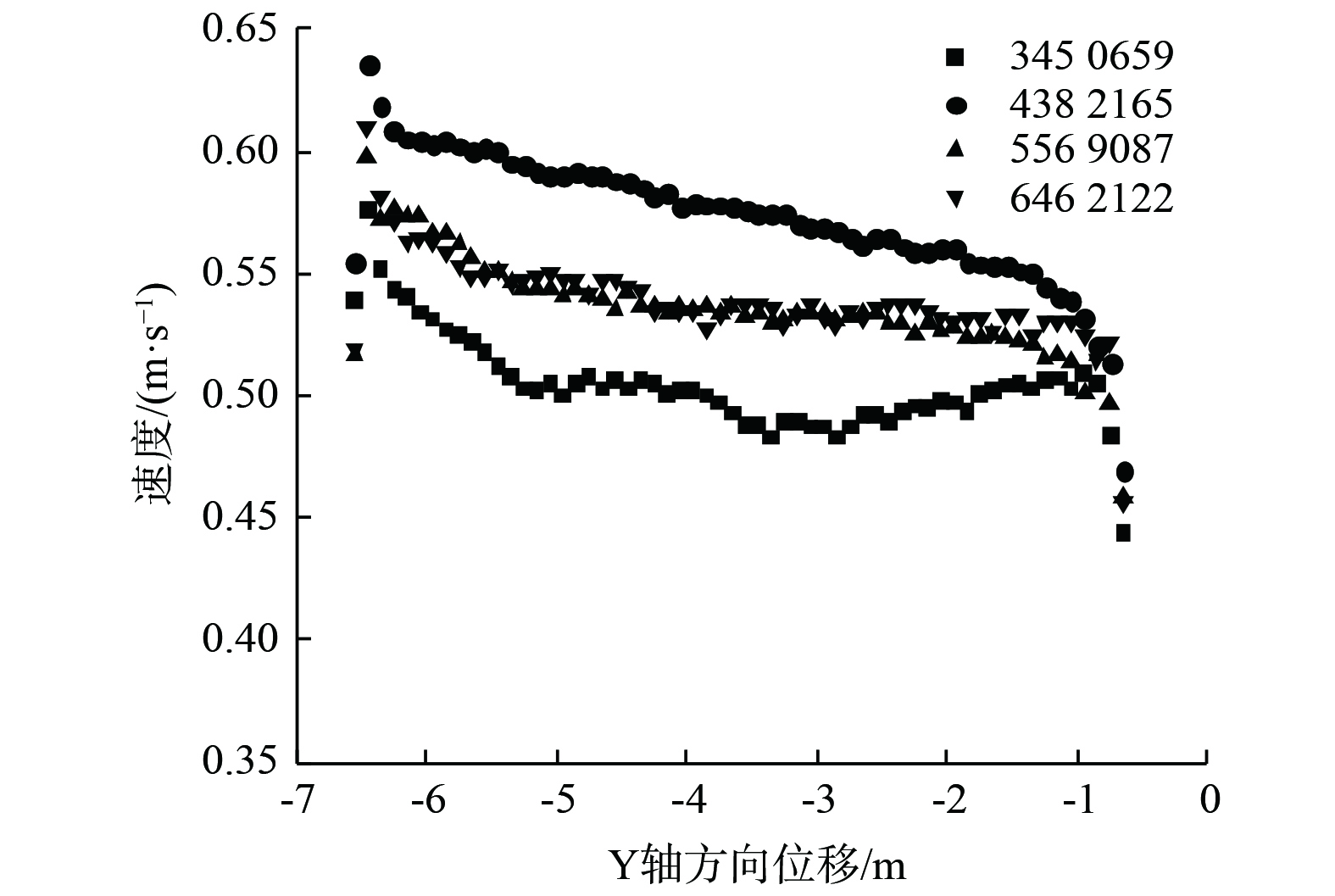
$ \varepsilon $ 模型和褶皱等效为圆筒滤袋的方法可用于袋式除尘器的数值模拟计算。2)网格无关性检验。为避免网格数量对数值计算准确性的影响,各模型在划分网格的过程中均进行了网格无关性检验。采用袋长为6 m的除尘器模型为例来进行网格无关性检验。分别取3 450 659、4 382 165、5 469 087,以及6 462 122网格数量进行流场数值模拟。取除尘器内部中心位置线,在线上不同位置取50个点对速度进行监测(见图6)后发现,当格数为5 469 087与格数为6 462 122时的速度结果相近,计算结果对网格数量变化不敏感,在网格数为5 469 087时就达到了网格无关的阈值。考虑计算效果和效率, 网格数为约540万可满足计算需求。
-
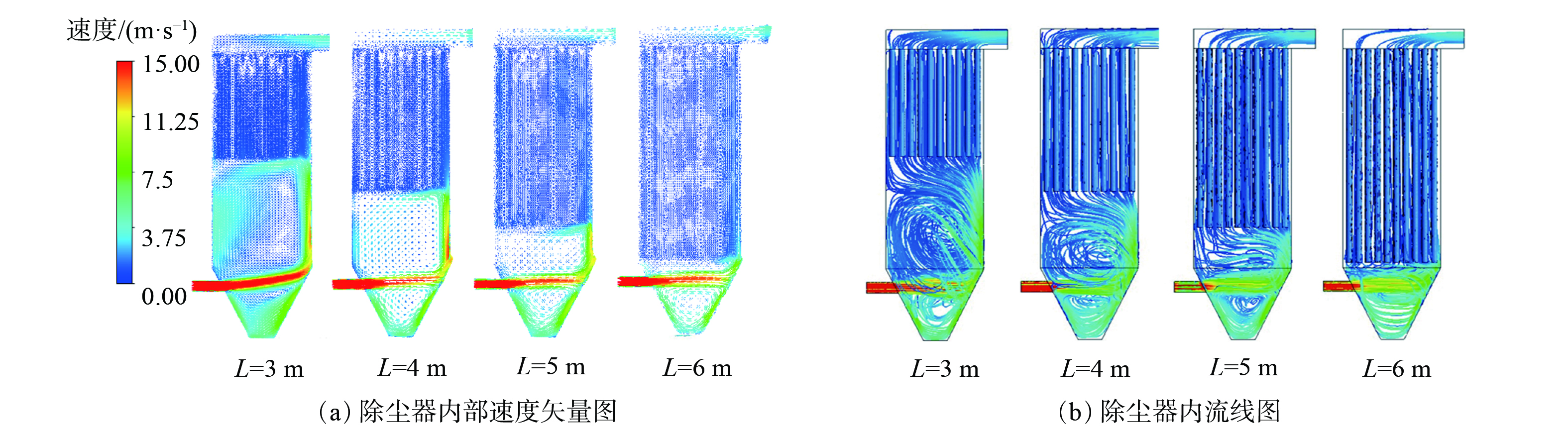
1)袋长对除尘器内部流场影响。首先对4种不同袋长袋式除尘器的速度场进行分析,图7为袋长L=3、4、5、6 m除尘器内部(Z=0)截面的速度矢量图与流线图。除尘器内速度较高处主要集中在入口附近、出口附近、滤袋间隙的下端。除尘器入口处风速最大,气流进入除尘器后卷吸内部气流向前运动,速度逐渐衰减,至对侧壁面后,转而向上和向下运动。袋长L=3 m的除尘器内部空间较大,进口气流速度衰减较慢。粉尘运动至对侧壁面仍保持高速,向下运动的气流在灰斗中形成高速涡旋。灰斗中远离进风口一侧壁面气流速度较高,向上的气流在内部空间运动形成大的涡旋,使得滤袋下部箱体风速极不均匀。涡旋的存在会使处于其中的粉尘颗粒不易沉降。袋长L=4 m时内部空间减小,其灰斗中气流漩涡速度减小,滤袋下部箱体气流漩涡尺寸、速度均有所减小。袋长L=5 m时进风口进入的气流速度不断衰减,此时向上运动的气流不会在箱体内形成漩涡。袋长增至6 m 后,除尘器灰斗内气流回流速度减小,箱体内速度分布更均匀。
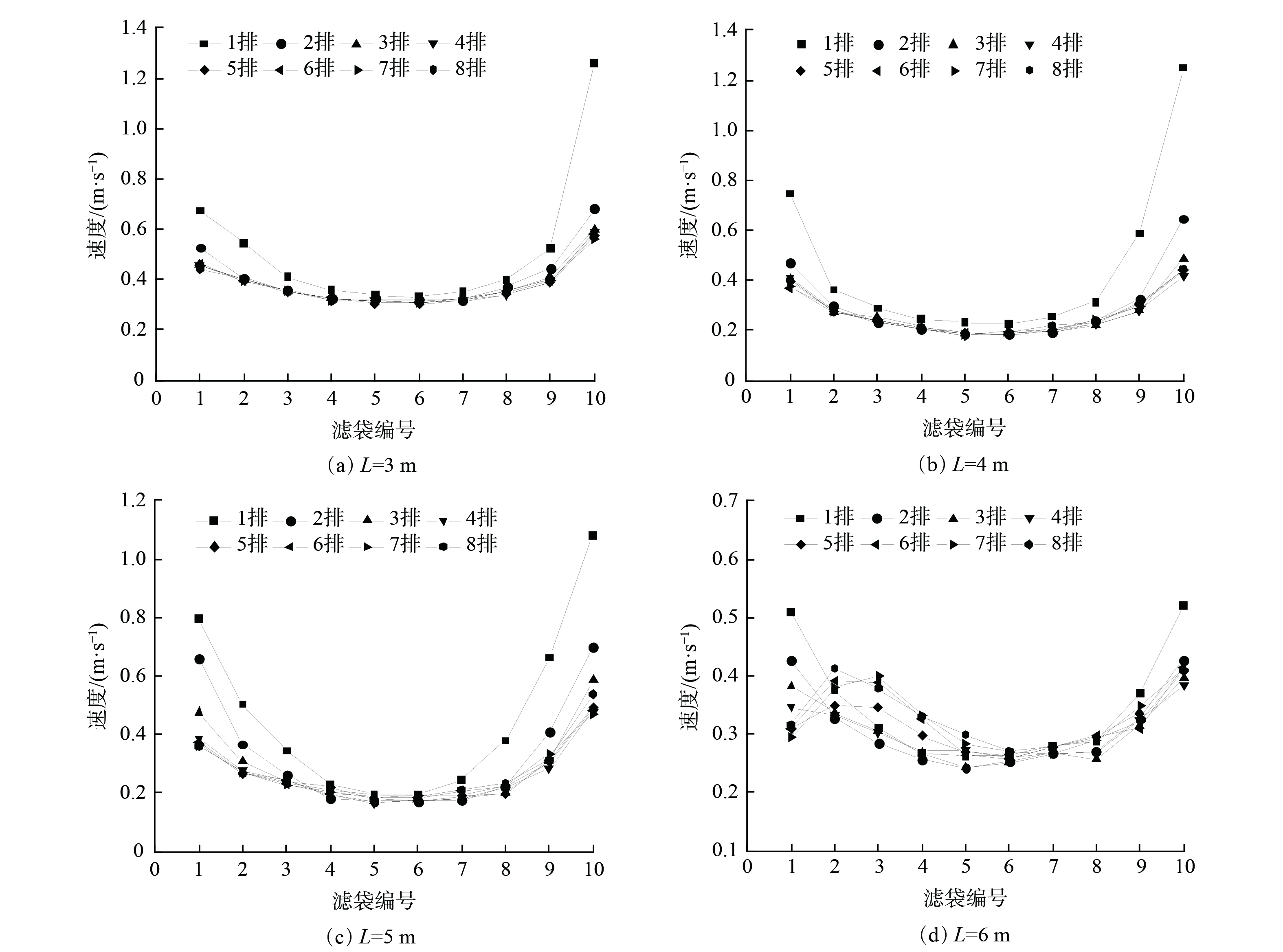
为了解气流进入滤袋空间时的速度场和流量分配的均匀性,对4种袋长除尘器中滤袋底部速度场进行分析。选取4种袋长滤袋下50 mm处平面作为监测面,该处各点Y方向上的气流速度可反映除尘器内气流能否均匀进入每个滤袋。监测点按照15排10列均匀布置共150个,1~10列按照从进口端到远离进口端进行编号,垂直于入口方向从前到后依次为第1排至第15排(入口在左侧)。
因为结构对称,取1~8排滤袋下方50 mm位置Y方向上的速度进行分析,速度分布如图8所示。各长度滤袋底部Y方向上风速整体呈现凹形分布。当袋长L=3 m时,除尘器中滤袋底部向上风速最高,且第1排、第2排各位置滤袋底部向上风速明显高于其他排。而远离入口处滤袋(第1排10号滤袋底部)向上风速最大为1.26 m·s−1,靠近入口处滤袋向上风速小于远离入口侧。随滤袋长度的增加,除尘器内滤袋底部空间减小,进入各滤袋的风速减小。当袋长L=4、5 m时,除尘器中靠近前侧壁面(第1~2排)滤袋底部向上风速大于其他排滤袋,最大速度分别为1.25、1.08 m·s−1。当袋长L=6 m时,除尘器中间位置靠近进风口处(第5~8排的1号滤袋)底部向上风速略小于每排2号、3号滤袋。之后,向上风速逐渐降低,各排中间位置滤袋速度较低,随滤袋位置越远离进风口速度越高。靠近进风口滤袋底部向上风速最大值为0.51 m·s−1,远离进风口处最大值为0.52 m·s−1。这表明进入滤袋区域的风速最大与最小的差值减小,风速较为均匀。
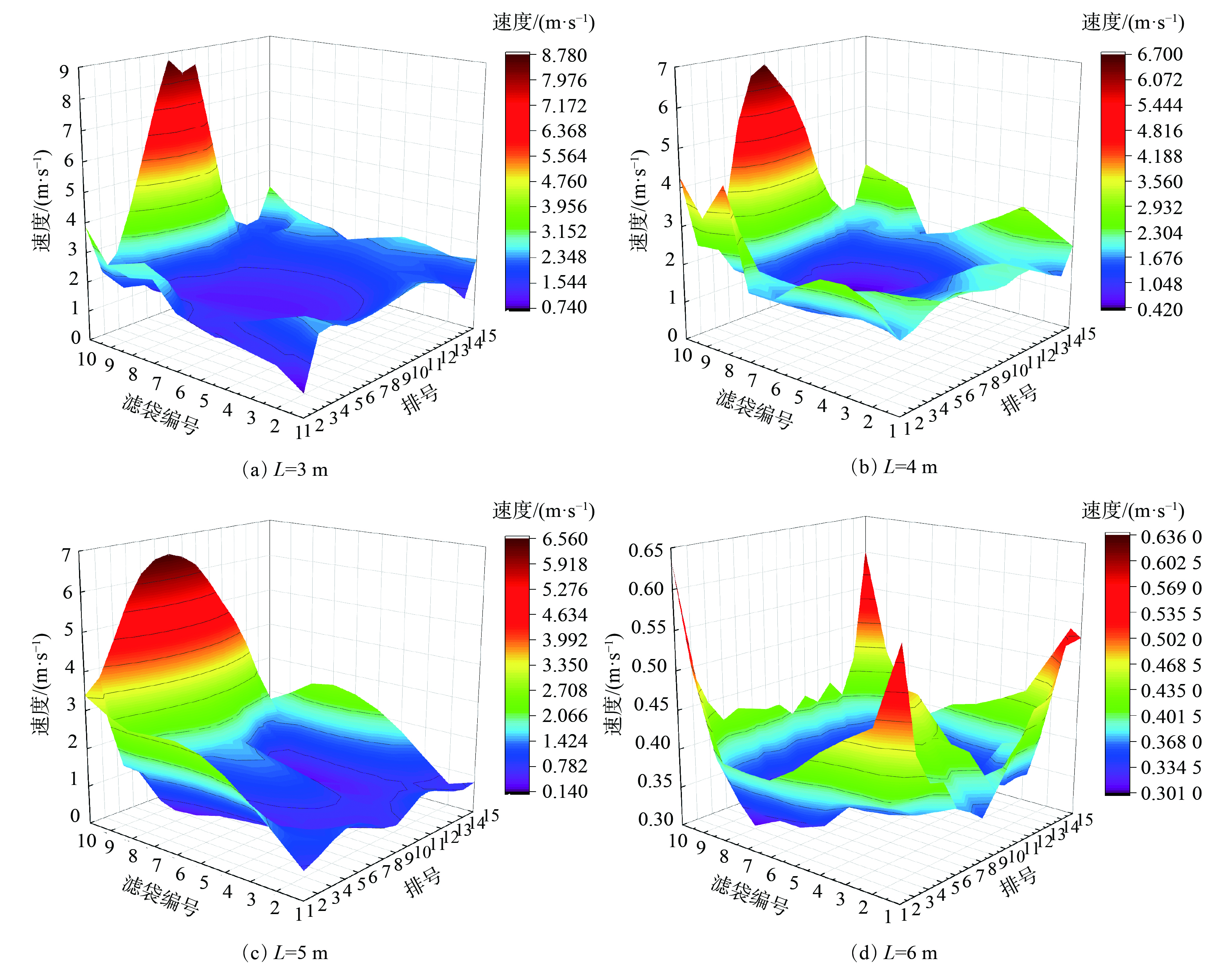
最后,按上述测点排布,对各除尘器入口上部截面速度场进行分析,截面位于除尘器灰斗上方50 mm。该处各点气流速度可以反映气流向上进入除尘器内部流场的均匀性。由图9可知,当袋长L=3、4、5 m时,除尘器此位置风速分布整体呈现前端小、后端大的状态,最大风速位于除尘器中间排远离进风口位置(第8~9排10号滤袋下方对应位置),速度分别为8.78、6.70、6.56 m·s−1,且滤袋长度越短,此位置风速越大。除尘器靠近两侧壁面(第1排、第2排、第14排、第15排)风速大于中心位置。这是由于进风口截面与灰斗截面面积相差较大,当气流从进风管进入灰斗后动静压剧烈转换,而外加滤袋缩短会导致除尘器内部空间增大,入口射流发展受滤袋的影响小,气流运动到入口对侧仍保持较高速度,且大部分气流会沿壁面向上运动,造成后壁面、侧壁面速度大。当袋长L=6 m时,平面内部速度分布均匀,最大、最小速度分别为0.636、0.301 m·s−1,最大速度位于靠近除尘器四周滤袋。以上分析可知,除尘器内袋长变短会造成气流分布的不均匀,不利于除尘器的过滤过程。
2)袋长对粉尘沉降影响。在袋式除尘器运行中,粉尘直接沉降在灰斗中的百分比(即沉降率)越高,滤袋的过滤负担越小。本研究在模拟除尘器稳态流场的基础上,加入颗粒物进一步研究不同袋长对粉尘在灰斗中沉降的影响。图10为粉尘分别进入袋长3 m和6 m除尘器后,在2 s时间内不同时刻粉尘颗粒的运移情况。
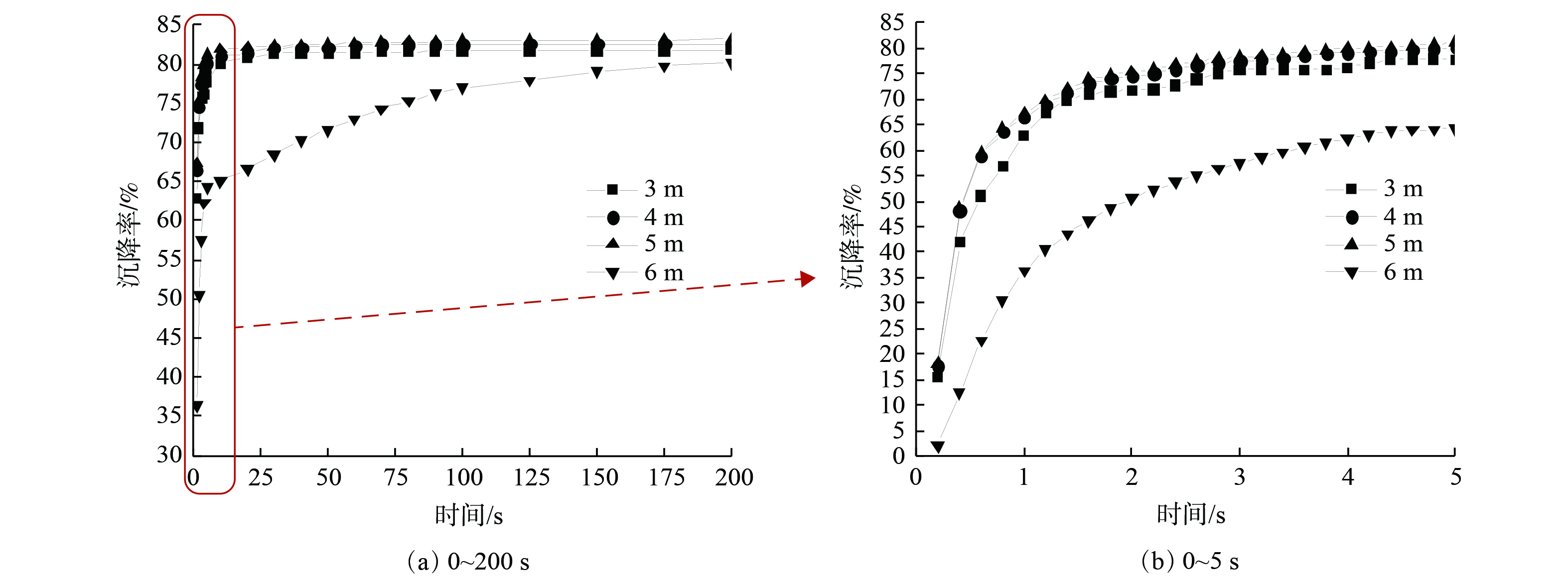
图10表明,袋长3 m时,较大粒径颗粒物在灰斗中直接沉降,较小颗粒物跟随气流逐渐向滤袋运动。而袋长6 m时,大颗粒粉尘在灰斗内涡流的作用下沉降速度慢,且一部分颗粒物直接落在滤袋上,减少了沉降率。图11为不同时刻、不同袋长除尘器内部沉降至灰斗中粉尘占总粉尘的百分数,即沉降率随时间的变化。在初始阶段(T=0.2 s),当袋长L=6 、5 、4 、3 m时,除尘器内沉降率分别为2.1%、18.16%、17.66%和15.66%。在除尘器运行约100 s后,粉尘在灰斗中的沉降率基本达到稳定状态。此时的沉降率分别为76.99%、82.95%、82.51%、81.62%。分析发现,滤袋从6 m缩短为5 m后,由于有一定空间使大粒径粉尘颗粒沉降,粉尘在灰斗中的沉降率明显增加,但继续缩短滤袋长度至4 m和3 m,沉降率不仅没有增加反而会减小。由图7和图8可知,当袋长L=6 m时,除尘器内气流由进气口进入,在灰斗中形成涡旋之后上升至滤袋,气流漩涡使粉尘不宜在灰斗中沉降并可能导致已沉降的粉尘颗粒被气流卷起。由于除尘器内部空间较小,粉尘会直接落在滤袋上从而导致落入灰斗中的粉尘量较低。当袋长L=3 m时,气流在灰斗中产生涡旋的速度较高,高速气流可带动粉尘向除尘器上部运动,气流在滤袋下部空余箱体内也会形成涡旋,小粒径粉尘颗粒跟随气流在除尘器内运动,粉尘颗粒在除尘器空间内停留时间增加,导致粉尘在灰斗中的沉降率降低。因此,对于下进风式除尘器而言,滤袋底部与进风口保持一定距离有利于粉尘的沉降,但并非除尘器内部空间越大粉尘越易沉降至灰斗。对于本研究所分析的除尘器而言,当袋长L=5 m时粉尘在灰斗中的沉降率达到最佳。
-
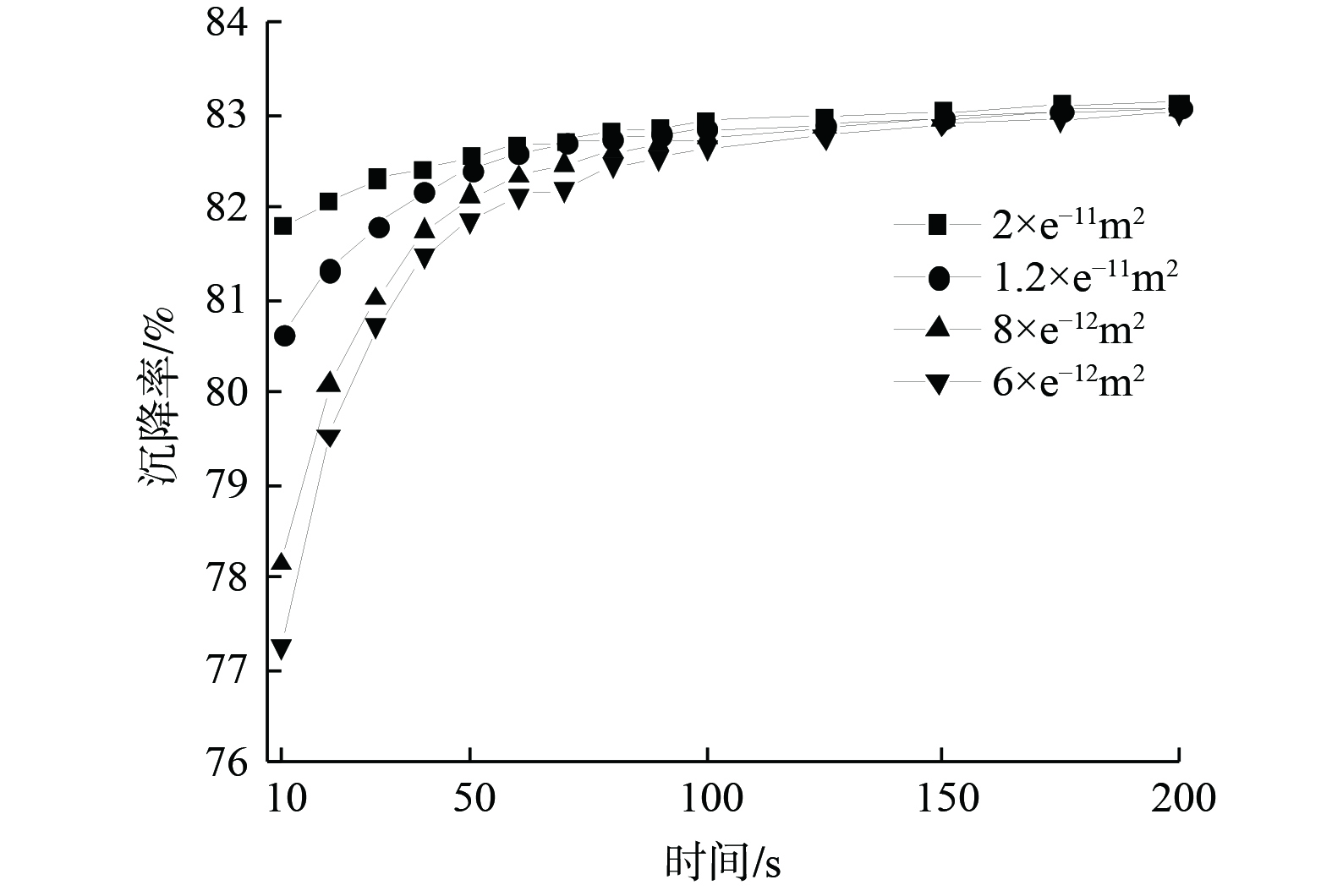
在除尘器实际运行过程中,随着粉尘的附着,荷尘滤袋的整体渗透率会逐渐降低。为分析荷尘过程中除尘器内部流场及粉尘的沉降情况,用整体渗透率的不同表征过滤的不同阶段。由前文分析可知,袋长L=5 m的除尘器中粉尘在灰斗中沉降率最佳,故取此模型进行研究。同前文设定保持一致,初始清洁状态滤袋渗透率为2×e−11 m2,此时的滤袋阻力为300 Pa。在模拟除尘过程中,滤袋的阻力产生变化,根据达西公式计算并设定整体渗透率。当阻力分别为500、750、1 000 Pa时,滤袋的渗透率分别为1.2×e−11、8×e−12、6×e−12 m2,表示除尘器逐渐荷尘至清灰之前的状态。图12为不同渗透率滤袋除尘器内粉尘沉降率对比。在除尘的初始阶段滤袋处于清洁状态,滤袋渗透率较大除尘器内部粉尘沉降到灰斗的比例较大。随着粉尘的附着,滤袋渗透率变小,粉尘的沉降率也呈降低趋势。在沉降稳定阶段(T=100 s)4种渗透率滤袋沉降率分别为82.95%、82.87%、82.76%和82.64%,故在稳定阶段沉降效果相差不大。
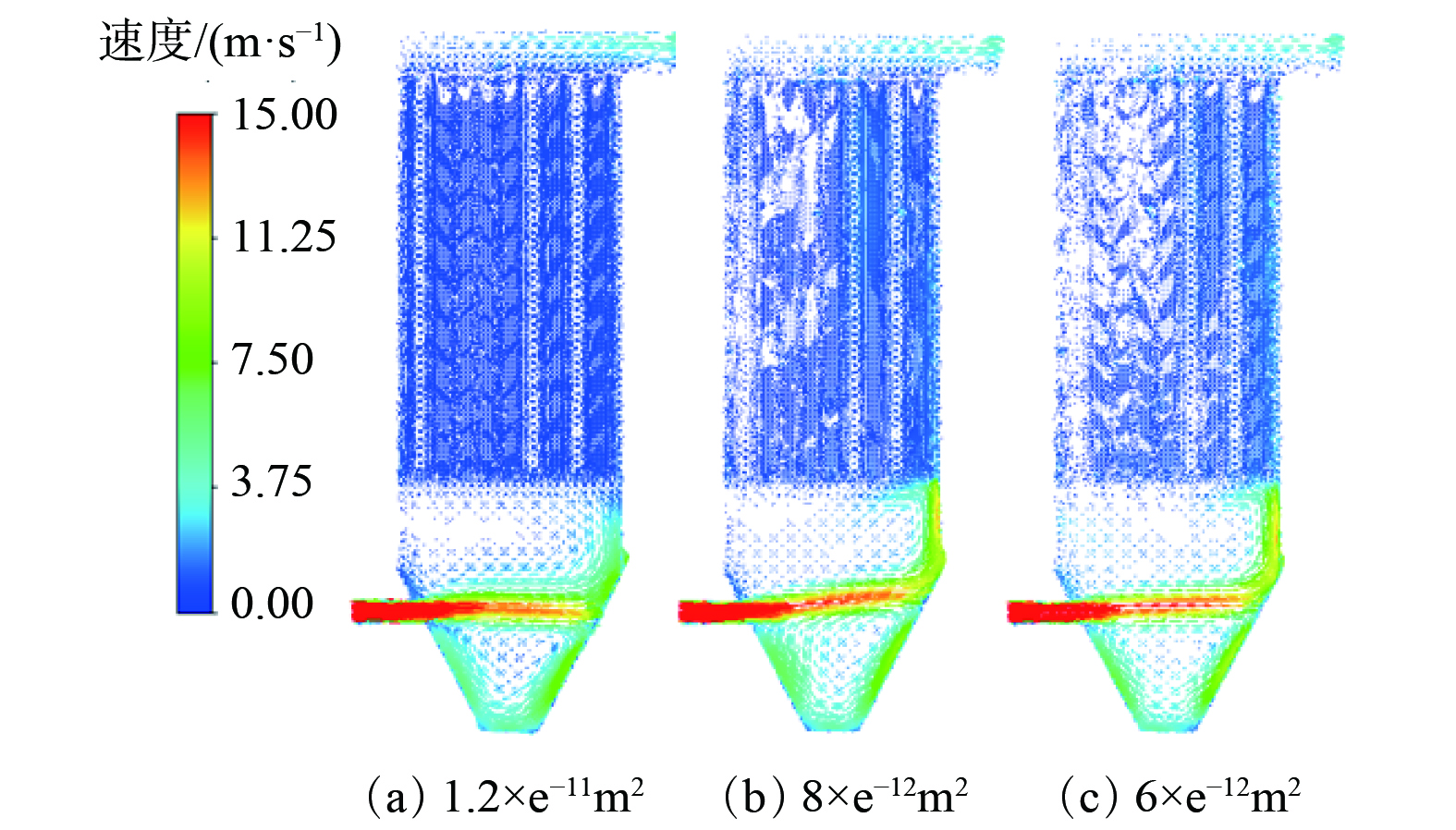
图13为袋长L=5 m滤袋渗透率为1.2×e−11、8×e−12、6×e−12 m2时除尘器内部速度矢量图(渗透率2×e−11 m2见图7(b))。随着滤袋渗透率的减小,除尘器内部滤袋与滤袋之间速度分布呈现远离进风口处速度增大、靠近进风口处速度减小的趋势。即由于滤袋渗透率减小,除尘器室内流场均匀性降低,导致粉尘在灰斗中沉降率降低。
在除尘器实际运行过程中,滤袋渗透率会随时间而变化,且随着喷吹过程的进行呈现循环。对于入口粉尘浓度大,喷吹周期短的情况,可能达不到本研究模拟条件下的沉降稳定阶段,渗透率就已发生了较大变化,沉降率的增加会受到抑制。
-
1)多孔阶跃边界条件和Realizable k-
$ \epsilon $ 模型计算袋式除尘器的阻力特性与流场分布具有准确性。运用流量当量直径法可将褶皱滤袋简化为圆筒滤袋,N=8褶的褶皱滤袋渗透率近似于相同工况条件下圆筒滤袋的1.6倍。2)滤袋长度对除尘器内部流场有较大影响。滤袋越短除尘器内部流场越不均匀,气流易在除尘器空间内部、灰斗中产生涡旋,不利于粉尘沉降和滤袋的均匀荷尘且除尘器内远离进风口一侧的滤袋会承担更多风量并受到高速气流冲击,进而影响滤袋的使用寿命。
3)不同袋长除尘器中粉尘在灰斗的沉降率(η)为η(L=5 m)>η(L=4 m)>η(L=3 m)>η(L=6 m)。研究表明适当缩短滤袋有利于颗粒物的沉降,但进一步缩短滤袋并不能使沉降率增加。
4)滤袋渗透率对除尘器内部流场和粉尘沉降有一定影响。滤袋渗透率越大,除尘器内部滤袋与滤袋之间速度越均匀,粉尘更易沉降至灰斗。随着荷尘过程的进行,滤袋渗透率减小,粉尘在灰斗中的沉降率也会减小。
数值模拟滤袋长度对除尘器流场及粉尘沉降的影响
Numerical simulation of the influence of filter bag length on bag filter flow field and dust settling
-
摘要: 利用数值模拟方法,探究袋式除尘器中圆筒滤袋改为褶皱滤袋后,滤袋长度变化对除尘器内部流场及粉尘在灰斗中沉降的影响。结果表明:圆筒滤袋改为褶皱滤袋可显著降低系统阻力,有利于系统节能;下进风式除尘器箱体中,滤袋越短除尘器内部的气流分布越不均匀,气流易在除尘器箱体空间及灰斗中产生涡旋,除尘器内部远离进风口一侧的滤袋会承担更多风量并受到高速气流冲击;在袋长(L)分别为3、4、5、6 m的除尘器内,粉尘在灰斗中沉降率(η) 为η(L=5 m)>η(L=4 m)>η(L=3 m)>η(L=6 m)。这表明袋底距入口太近不利于粉尘沉降,粉尘直接运动至滤袋,反而会增加滤袋的过滤负担,故滤袋长度L=5 m时粉尘在灰斗中的沉降率最佳。然而,进一步降低滤袋长度不能提高粉尘的沉降率,滤袋渗透率越大,除尘器内部流场速度分布越均匀,粉尘更易沉降至灰斗。本研究结果可为下进风袋式除尘器的袋长设计提供参考。Abstract: Numerical simulation method was used to analyze the influence of changing filter bag length on internal flow field in the bag filter, and dust settling in the ash hopper after the cylindrical filter bag was changed to the pleated filter bag.The results showed that changing cylindrical filter bag into pleated filter bag could significantly reduce the system pressure drop, which was beneficial to the system energy saving. In the case of down inlet bag filter, the shorter the filter bag was, the more uneven the air flow distribution in the bag filter was, and the air flow was easy to vortex in the bag filters space and ash hopper, and the filter bag on the side of the bag filter far from the air inlet would bear more air flow and be impacted by high-speed air flow. In the bag filters with a length (L) of 3,4,5,6 m,the order of dust settling rate(η) in the ash hoppers was η(L = 5 m) > η(L = 4 m) > η(L = 3 m) > η(L = 6 m), which indicated that the bottom of the bag was too close to the entrance, and it was not conducive to dust settling. When the bag length was at L=5 m, the dust settling rate in the ash hopper was the best, but further reducing bag length could not improve the dust settling rate. The greater the filter bag permeability was, the more uniform the velocity distribution of the flow field in the bag filter was, and the dust was more likely to settlle to the ash hopper. The research results can provide guidance for bag length design of down inlet bag filter.
-
Key words:
- bag filter /
- numerical simulation /
- length of filter bag /
- permeability /
- dust settling
-
-
表 1 粉尘的粒径范围分布
Table 1. The range of particle size distribution
粒径/μm 百分比/% 10 14.7 30 27.4 70 24.5 100 14.3 150 11.7 300 7.4 -
[1] 杜然, 舒刚, 文福, 等. 钢铁企业矿焦槽除尘超低排放改造方案分析[J]. 建筑热能通风空调, 2020, 39(1): 102-105. doi: 10.3969/j.issn.1003-0344.2020.01.025 [2] 张波波, 赵宝杰, 王志永. 高效褶皱布袋在焦炉装煤除尘器中的应用[J]. 燃料与化工, 2019, 50(6): 25-26. doi: 10.16044/j.cnki.rlyhg.2019.06.010 [3] 赵金怀, 钱磊. 褶皱滤袋技术在钢铁超低排放改造中的应用[J]. 工业安全与环保, 2019, 45(12): 85-87. [4] 孙志钜. 燃煤锅炉布袋除尘器改造与褶皱滤袋的应用//中国环境保护产业协会袋式除尘委员会[J]. 全国袋式除尘技术研讨会论文集. 天台, 2021: 135-138. [5] 王锦. 针刺优氪迅滤筒技术及其在水泥粉磨系统的应用[J]. 新世纪水泥导报, 2021, 27(1): 78-80. doi: 10.16008/j.cnki.1008-0473.2021.01.013 [6] THERON F, JOU A, LAU L. Numerical and experimental investigations of the influence of the pleat geometry on the pressure drop and velocity field of a pleated fibrous filter[J]. Separation and Purification Technology, 2017, 182(56): 69-77. [7] JEONG U K, JUN H et al. Effective filtration area of a pleated filter bag in a pulse-jet bag house[J]. Powder Technology, 2017, 311: 522-527. doi: 10.1016/j.powtec.2017.02.013 [8] 刘含笑, 李文华, 杨倩, 等. 袋式除尘器单滤袋流场模拟[J]. 电力科技与环保, 2019, 35(1): 16-18. doi: 10.3969/j.issn.1674-8069.2019.01.006 [9] 黄治文. 袋式除尘器长袋的流场特征的数值模拟[D]. 南昌: 南昌大学, 2018. [10] SANGCHEL P, YUN H J, JOONMOK S, et al. Non-uniform filtration velocity of process gas passing through a long bag filter[J]. Journal Of Hazardous materials, 2019, 365: 440-447. doi: 10.1016/j.jhazmat.2018.10.098 [11] THOMAS W C P, FELIOE B M, FABIO D A R P, et al. The influence of the fabric filter layout of in a flow mass filtrate[J]. Journal Of Cleaner Production, 2016, 111: 117-124. doi: 10.1016/j.jclepro.2015.09.070 [12] 毛锐, 刘根凡, 邓翔等. 布袋除尘器结构改进的数值模拟研究[J]. 环境工程, 2015, 33(3): 77-81+91. doi: 10.13205/j.hjgc.201503018 [13] 丁倩倩, 李珊红, 李彩亭, 等. 滤袋长度对袋式除尘器内流场影响的数值模拟研究[J]. 环境工程学报, 2015, 9(11): 5521-5526. doi: 10.12030/j.cjee.20151162 [14] 方璨, 钱付平, 叶蒙蒙, 等. 无纺针刺毡滤料褶式滤袋的阻力特性分析[J]. 过程工程学报, 2020, 20(3): 285-293. doi: 10.12034/j.issn.1009-606X.219217 [15] 王福军. 计算流体动力学分析—CFD 软件原理与应用[J]. 北京:清华大学出版社, 2004: 125-127. [16] 任美桃. 下进风袋式除尘器内部流场模拟与结构优化[D]. 西安: 西安建筑科技大学, 2018. [17] FLUENT 6.3. 26, User’s Guide, Fluent Inc. [R/OL]. https://www.academia.edu/43373884/FLUENT_6_3_Users_Guide. [18] 李为浩. 直通式下进风袋式除尘器内流场研究及结构优化[D]. 太原: 太原理工大学, 2016. -
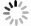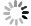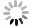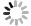


 下载:
下载: