-
近地面高浓度臭氧(O3)会增强大气氧化性, 加重城市环境空气污染, 长期处于高浓度臭氧环境下会诱发心血管和呼吸系统疾病[1-2]. 准确预测臭氧浓度能够为臭氧防控治理提供重要支持, 及时污染预警可为居民出行决策提供建议, 降低健康影响. 臭氧浓度与前体物排放、气象、地形等因素密切相关, 具有高度复杂性和非线性变化特征[3], 存在着显著的时空关联特征[4]. 如何有效学习臭氧浓度分布的时空关联特征, 并用于臭氧浓度预测已成为关注的焦点.
目前大气臭氧浓度预测的方法主要有如下3种方法:(1)基于物理化学反应机制的空气质量模式[5-7], 该模式基于污染源排放清单、气象条件和大气边界条件, 模拟污染物在大气环境中的物理化学变化过程获得预测结果, 但该方法计算量大, 特征提取困难且运行成本高[8]. (2)基于统计学理论的预测模型[9-12], 该类统计方法对时间序列数据特征提取能力有限[13], 导致预测精度偏低且仅能实现较短步长预测. (3)基于机器学习算法的数值预测方法, 目前支持向量机算法及其改进算法被广泛应用于大气污染物浓度预测中[14-17]. 随机森林算法可以处理高维度数据并且可以得到变量重要性[18-20], 在大气污染物浓度预测领域取得了一定的成果. 深度学习算法[21-26]是机器学习领域最新的发展成果, 可深层次提取数据特征, 较好捕捉数据间的非线性关系. 深度学习中, 长短期记忆神经网络(long short-term memory neural network, LSTM) [27]能够提取时间序列数据的变化特征, 不受传统循环神经网络(recurrent neural network, RNN)梯度消失的影响[28], 同时具有序列到序列的多步预测能力. 有研究[29-31]使用LSTM模型预测臭氧浓度, 但LSTM模型无法考虑站点的空间关联影响, 导致模型预测准确度不高. 将 LSTM与卷积神经网络(convolutional neural network, CNN)[32-33], 耦合可处理空间信息, 从而更准确预测臭氧浓度.CNN适用于处理欧式空间数据, 在处理臭氧浓度分布这类非欧式空间数据时表现较差;而图卷积神经网络(graph convolutional neural network, GCN)[34]基于图傅里叶变换及拉普拉斯矩阵, 能够更好提取臭氧浓度分布这类非欧式空间数据特征. 因此, 将LSTM与GCN耦合能够捕获臭氧浓度的时空依赖关系, 相较于单独使用一种模型, 耦合模型预测准确性更高.
本研究建立了LSTM与GCN耦合的臭氧小时浓度预测模型, 并应用该模型预测北京市未来72 h臭氧浓度, 为臭氧预测预报提供了一种新的方法.
-
图卷积神经网络的基本思想是将臭氧浓度分布这类非欧式空间数据投影到欧氏空间, 进行卷积之后, 将结果返回至非欧氏空间. 其运算基于图傅立叶变换和拉普拉斯矩阵, 能够较好提取臭氧浓度空间分布特征.
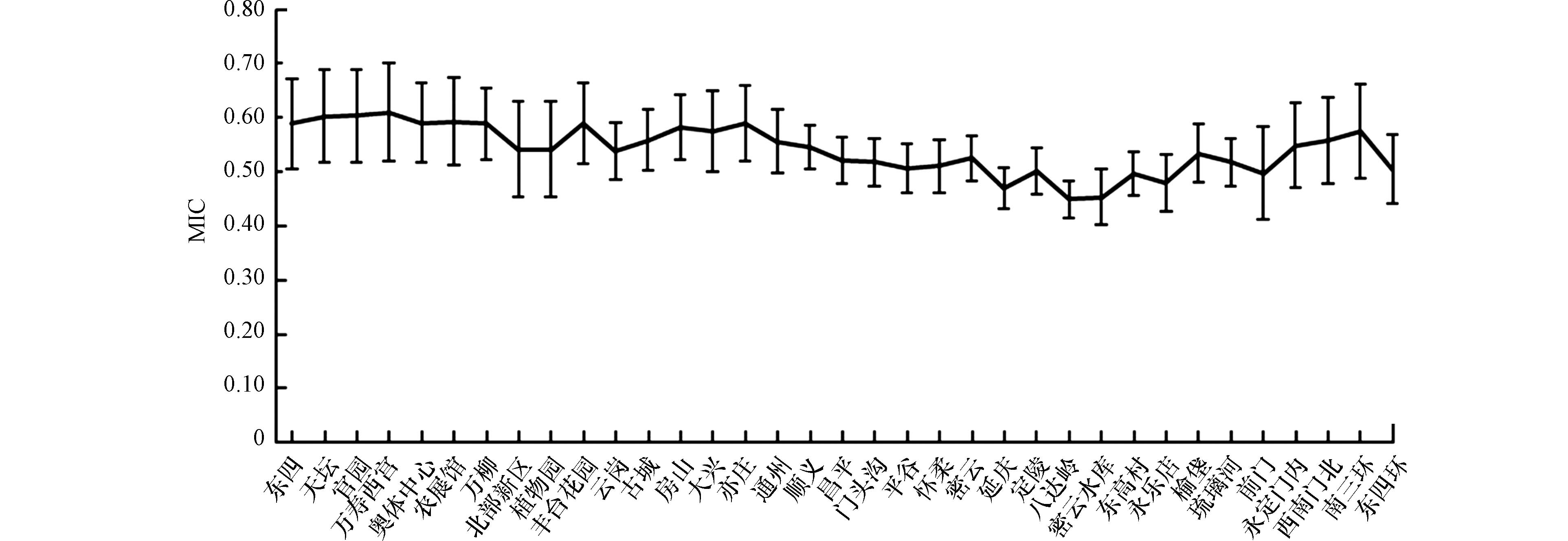
由于受浓度差和气象条件影响, 城市内部存在污染物空间传输作用. 最大信息系数(maximal information coefficient, MIC)[35], 是通过计算变量间联合分布概率来衡量变量的相似程度, 能较好检验出各种非线性关系. 通过计算城市空气质量站点臭氧监测浓度的最大信息系数, 可表征站点间的空间相关性. 根据北京市各空气质量站点臭氧监测浓度最大信息系数计算结果得图1. 各站点与其他站点最大信息系数均值均高于0.45, 标准偏差最大为0.09, 表明各站点臭氧监测浓度变化关联性较强.
t时刻N个空气质量监测站点的污染物浓度数据的空间分布可定义为一张非欧氏空间环境图G=(N, E, W), 如图2. 其中, N代表节点, 即空气质量监测站点; E代表节点间的连边, 即站点间的污染物传输关系;W代表节点间的邻接矩阵, 即监测站间距离的倒数;N个站点在时刻t的污染物浓度数据作为t时刻节点的特征矩阵. 连续多个时刻的污染物数据构成图序列, 将图序列输入至图卷积神经网络中, 利用其表示学习能力, 将各站点的空间关联关系建模.
本文建立的基于臭氧浓度数据的图结构中, 图中节点即空气质量监测站点, 其污染物浓度会受到其相邻站点污染物浓度状态的影响. 图卷积神经网络的计算过程可概括为三步:聚合、更新和循环. 其中, 聚合是指图卷积神经网络将相邻站点污染物浓度信息进行聚合, 提取污染物浓度空间传输特征; 更新是指完成聚合操作之后更新当前站点的污染物浓度状态; 循环是指将上述过程不断重复, 将观测时段内所有时刻站点的污染物浓度状态进行更新.
-
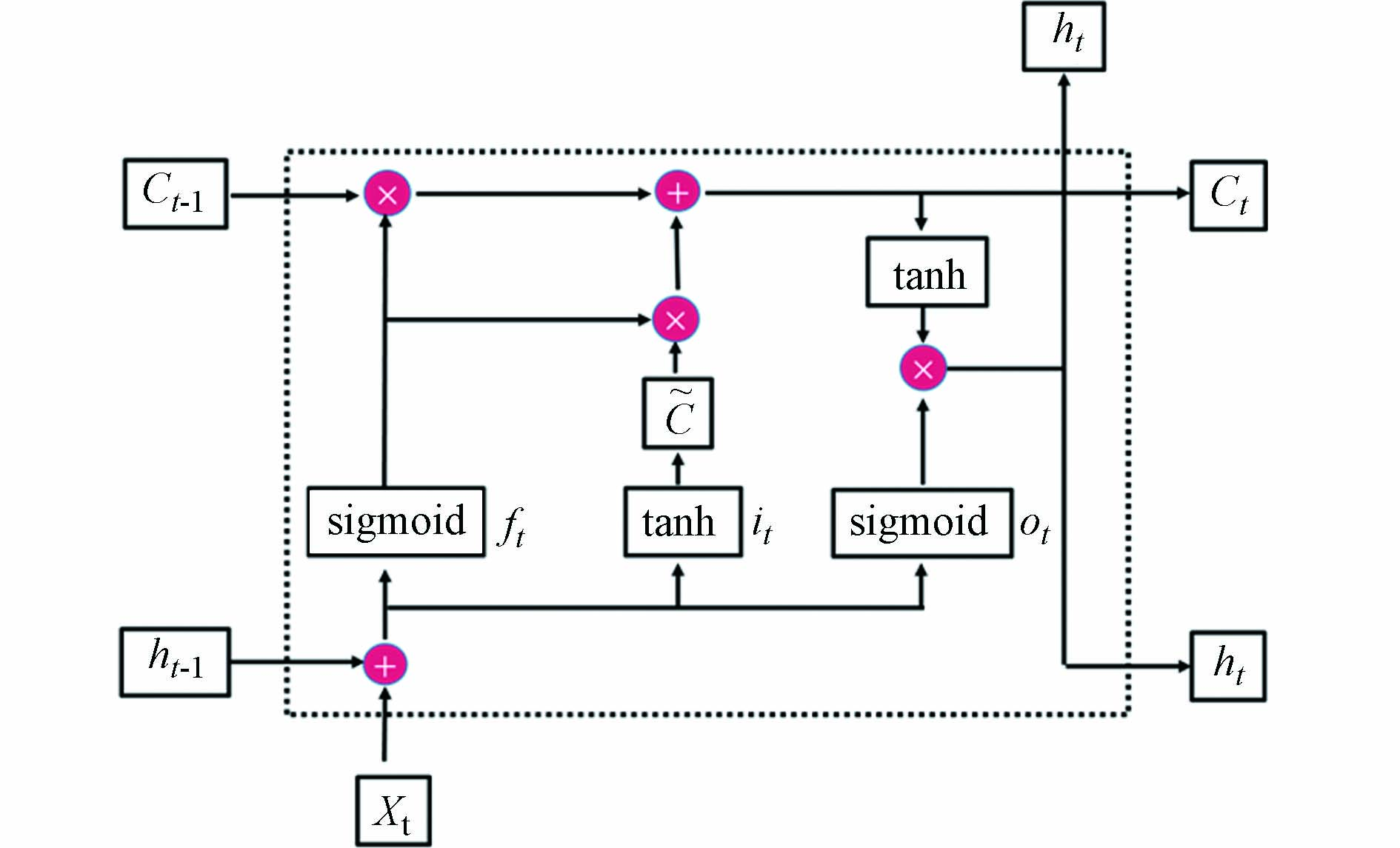
空气质量监测站点污染物浓度数据是典型的时间序列数据, 且某一站点当前时刻浓度与其上一时刻浓度存在相关性, 可依据时间依赖性对序列数据建模并提取历史数据特征. 与传统的RNN结构相比, LSTM能够有效避免梯度消失和爆炸的问题, 可更好提取长时间序列数据变化特征. LSTM通过引入门控机制选择性的通过信息, 使其具有添加和删除单元格信息的能力, 其单元结构如图3. 1个LSTM单元包括3个门, 分别是遗忘门(
$ {f_t} $ ), 记忆门($ {i_t} $ )和输出门($ {o_t} $ ), 如公式(1)—(6)所示.式中,
$ {W_f} $ ,$ {W_i} $ ,$ {W_c} $ ,$ {W_o} $ 表示在当前时刻LSTM单元的对污染物浓度信息的权重矩阵,$ {b_f} $ 、$ {b_i} $ 、$ {b_c} $ 、$ {b_o} $ 表示在当前时刻LSTM单元的对污染物浓度信息的偏置矩阵,$ {x_t} $ 代表当前时刻的污染物浓度,$ {C_t} $ 和$ {C_{t - 1}} $ 分别为当前时刻和上一时刻的污染物浓度变化信息,$ {h_t} $ 和$ {h_{t - 1}} $ 分别为当前时刻和上一时刻的污染物浓度信息,sigmoid,tanh为非线性激活函数. -
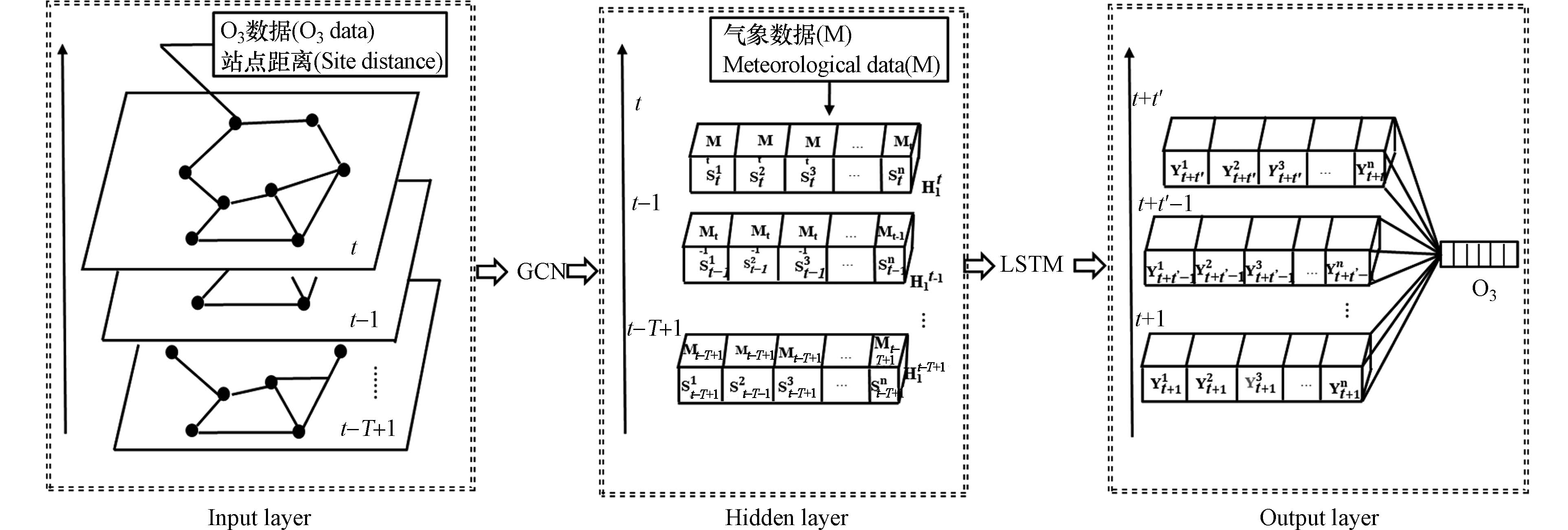
基于臭氧历史浓度数据和空气质量监测站点的空间关联图结构, 本文提出由GCN和LSTM网络联结而成的GCN-LSTM模型. 由于城市内部环境空气质量监测站点污染物浓度受周边站点污染物传输影响, 可利用图卷积神经网络提取历史时段各时刻的臭氧浓度空间传输特征, 实现空间和时间的耦合. 气象条件对污染物浓度变化具有重要影响[36], 本研究将气象数据作为独立的辅助变量, 与臭氧空间传输特征一同组成时间序列作为LSTM网络的输入. 模型整体架构如图4, 基于深度学习平台Tensorflow完成开发.
图4中T代表历史时间序列中所有时刻, 其中t代表当前时刻, t’代表未来时间序列中所有时刻. 模型具体运行步骤如下:(1)将各站点之间距离和t时刻各站点臭氧观测浓度输入图卷积神经网络, 提取站点间空间关系, 得到空间信息特征张量. (2)将t时刻气象数据M作为单独变量拼接到空间信息特征张量中, 得到张量H1. 此时, 张量H1既包含t时刻各站点之间的空间信息、臭氧观测浓度信息, 也含有气象信息. (3)在历史时间序列中每个时间步长重复上述操作, 最后将处理好的时空张量输入至LSTM模型进行训练, 可得到未来t’个时刻臭氧浓度. (4)为提高模型泛化能力, 在模型中添加随机失活层, 随机关闭一部分神经元.
-
模型构建过程中, 评价指标为均方根误差(root mean square error, RMSE)、准确率(accuracy rate, ACC)和平均绝对误差(mean absolute error, MAE). 使用平均相对偏差(mean relative bias, MRB)和均方根误差评价模型预测误差水平, 其定义如式(7)—(8). 其中,
$ n $ 代表样本数量,$ {o_i} $ 代表臭氧观测浓度,$ {p_i} $ 代表臭氧预测浓度, RMSE、MAE、MRB值越小, ACC值越大, 模型预测准确度越高. -
模型参数主要包括学习率、迭代次数、神经元随机失活比例、网络层数、学习时间步长、数据训练批次和神经元个数. 学习时间步长、数据训练批次、网络层数和神经元个数是GCN-LSTM模型中的重要参数, 不同的参数设置会较大影响预测精度. 在训练开始前, 手动将学习率设置为0.001, 迭代次数为1000次, 神经元随机失活比例为0.5, 通过设置对比实验确定参数最优值.
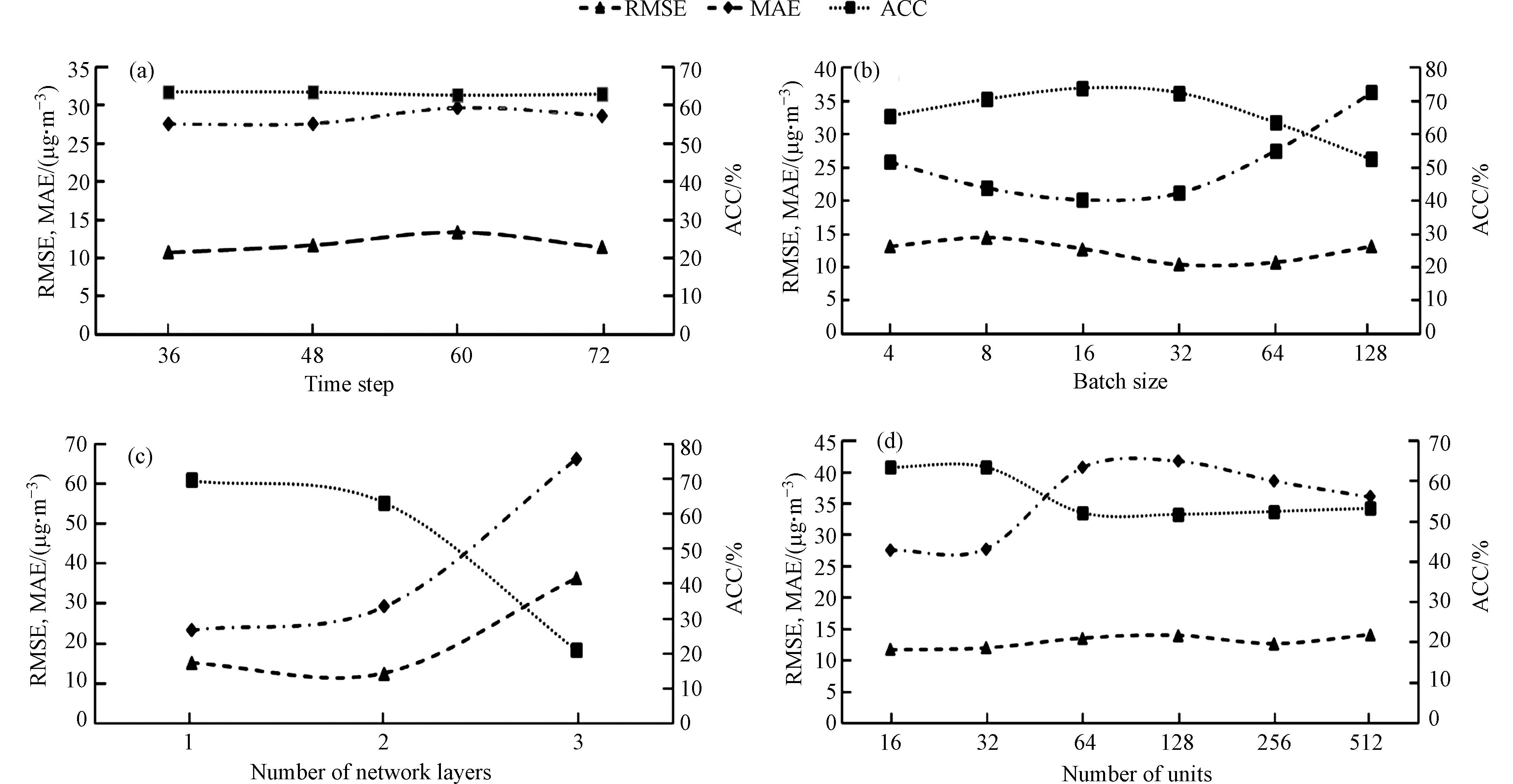
学习时间步长决定了模型在每个训练批次中所学习数据特征的数量, 如图5(a)所示, 当学习时间步长为36时, 模型预测误差最低, 准确率最高. 数据训练批次的大小决定了模型训练速度以及模型预测准确度, 如图5(b)所示, 当数据训练批次设置为32时, 模型RMSE, MAE以及ACC值相对最优.
模型所拟合数据的复杂程度决定了网络层数, 如图5(c)所示, 当网络层数设置为2时, 模型预测误差较小, 对数据拟合程度较好. 神经元个数设置过少将导致模型欠拟合, 无法学习数据变化规律; 神经元个数设置过多将导致模型过拟合, 模型的复杂度和计算难度会大大增加, 如图5(d)所示, 随着神经元个数的增加模型预测误差先降低后提高, 当神经元个数为32时, 模型预测效果最好.
本研究最终设定模型学习率为0.001, 神经元随机关闭比例为0.5, 迭代次数为1000次, 数据训练批次为32, 学习时间步长为36, 预测时间步长为12, 网络层数为2, 神经元个数为32.
-
本研究使用2020年1月—2021年8月北京市35个环境空气质量站点臭氧小时浓度观测数据、同期气象数据(温度、气压、风速、风向、降水、相对湿度和净日照辐射)和监测站点空间信息组成的数据集开展模型实际应用. 其中, 臭氧浓度观测数据来源于北京市生态环境监测中心(http://zx.bjmemc.com.cn), 气象数据来源于国家气象科学数据中心(http://data.cma.cn/).
经检验, 臭氧小时浓度观测数据缺失率为3.52%, 利用拉格朗日插值法填充缺失值. 将数据集归一化至[0, 1]并随机选取80%连续数据为训练集, 剩余20%数据为验证集.
-
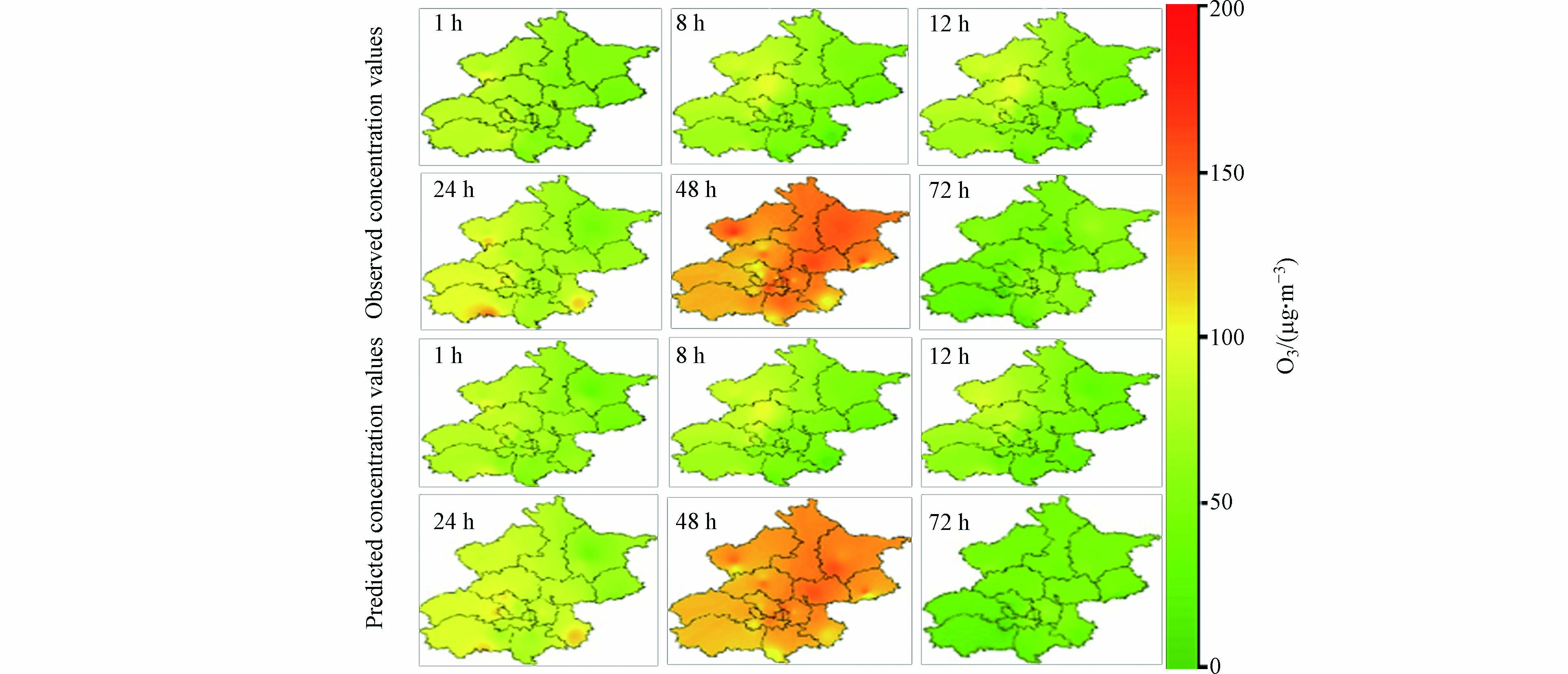
利用模型对北京市2021年9月4日—9月7日35个站点臭氧浓度进行预测, 将实际观测浓度与模型预测浓度输入至地理信息系统(ArcGIS), 利用反距离权重插值法进行插值分析, 得到臭氧观测浓度值与预测浓度值分布, 如图6. 从观测结果来看, 观测时段内北京市臭氧浓度在时间分布上有先上升后下降的趋势, 且空间分布存在一定差异. 从预测结果来看, 模型较好地预测出臭氧浓度的时间变化及空间分布趋势.
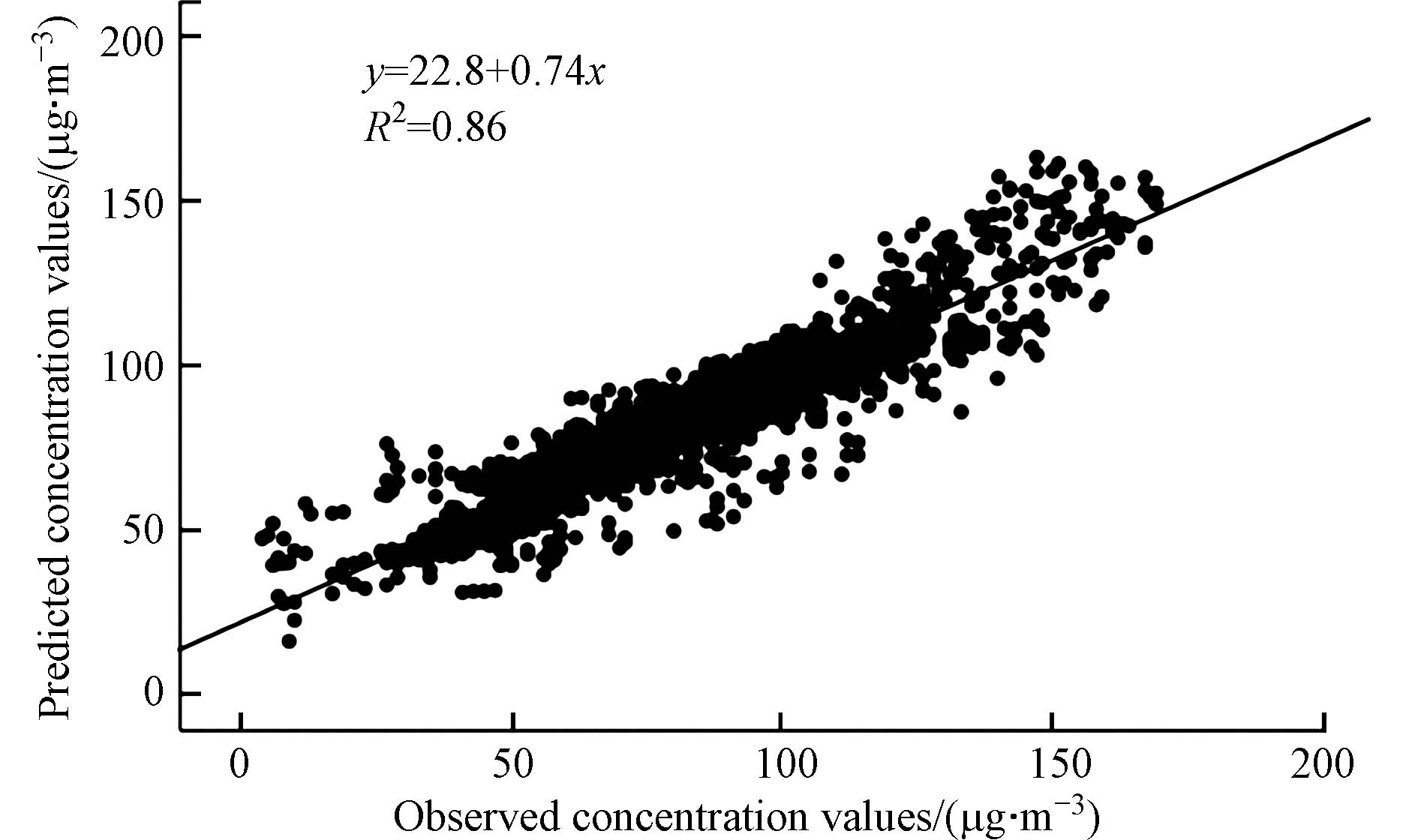
图7为模型臭氧预测浓度值与观测浓度值散点图. 预测值与观测值决定系数R2为0.86, 模型整体预测效果较好. 模型训练集与验证集中的决定系数R2分别为0.76和0.73, 从决定系数可以判断模型未出现过拟合或欠拟合现象, 表明该模型可较好用于城市大气臭氧小时浓度预测.
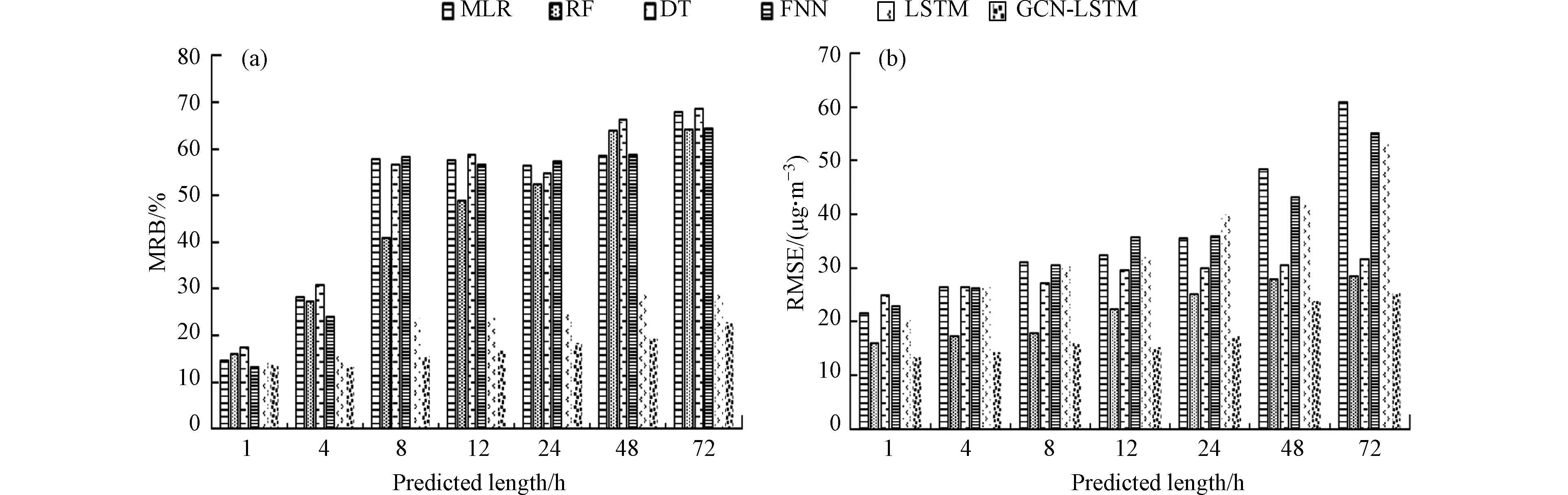
应用多元线性回归(MLR)、随机森林(RF)、决策树(DT)、前馈神经网络(FNN)、长短期记忆神经网络(LSTM)和图卷积-长短期记忆神经网络(GCN-LSTM)6种模型, 对北京市2021年9月4日—9月7日臭氧浓度进行预测(图8). 结果显示, GCN-LSTM预测24、48、72 h的MRB值分别为18.2%, 19.2%和22.9%, RMSE值分别为17.3, 23.7、25.4 μg·m−3, 可以看出GCN-LSTM模型预测效果最好. 相较于其他机器学习模型, 本研究提出的GCN-LSTM模型捕捉臭氧浓度时空关联特征的能力更强. GCN-LSTM模型利用图卷积神经网络和LSTM神经网络较好的刻画和捕捉了臭氧浓度时空关联特征及各因素对臭氧浓度的影响, 使模型对48—72 h污染物浓度预测准确度更高.
-
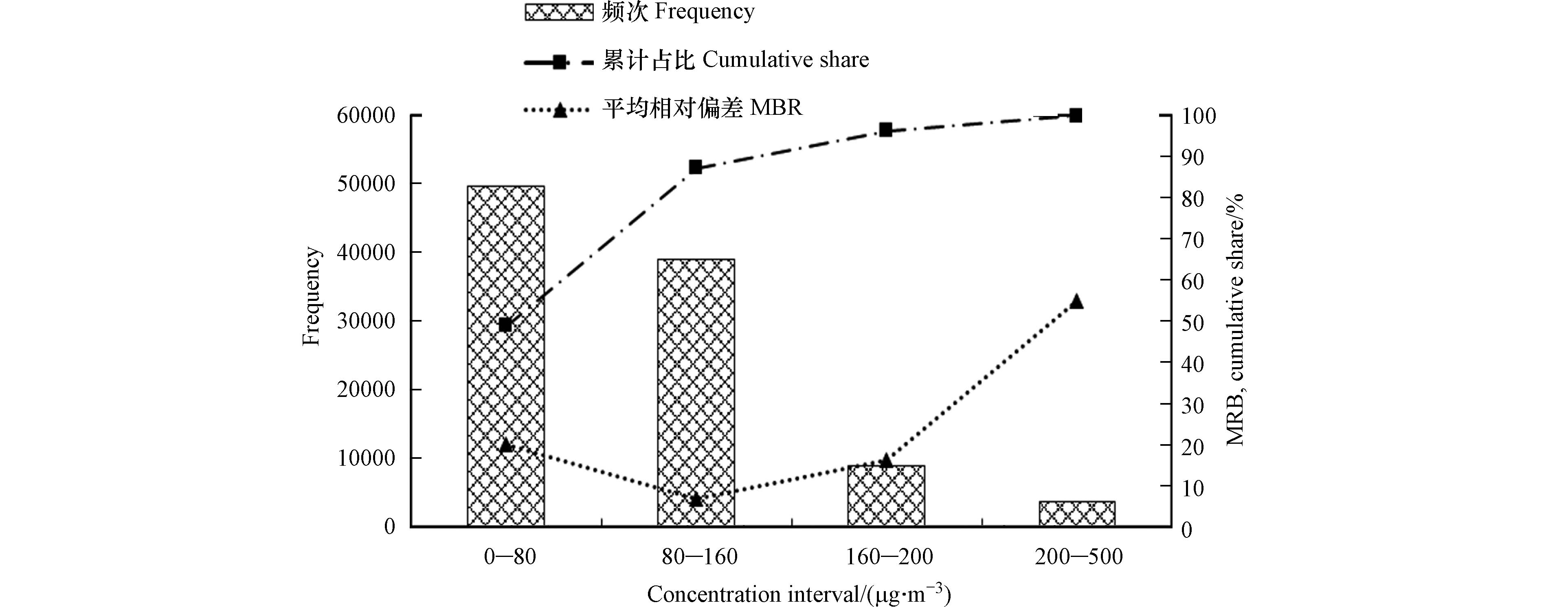
将测试集臭氧观测浓度分区间进一步对比发现, 当臭氧浓度介于0—80 μg·m−3、80—160 μg·m−3、160—200 μg·m−3和200—500 μg·m−3时, 模型预测浓度与观测浓度的平均相对偏差分别为20.1%, 6.9%, 16.4%和54.8%, 4个区间数据量分别占总数据量的48.9%、38.3%、9.1%和3.7%(如图9). 除臭氧观测浓度处于极大值情况外, 应用该模型对未来72 h臭氧浓度均可进行较好预测. 进一步分析预测臭氧浓度极大值时误差较大的可能原因, 一是图卷积神经网络对输入信号进行卷积操作时对突变信号进行了平滑处理, 导致模型较难捕捉浓度突变特征; 二是当预测浓度位于观测浓度最值之间时, 可使模型训练损失函数值最小, 符合模型优化隐藏层参数原则. 因此, 下一步研究中可在模型中增加拐点预测模块[37], 并输入更多相关变量, 通过筛选臭氧浓度突变数据及对应相关变量数据训练拐点预测模块, 对模型最终输出结果进行调整, 以减小预测误差.
-
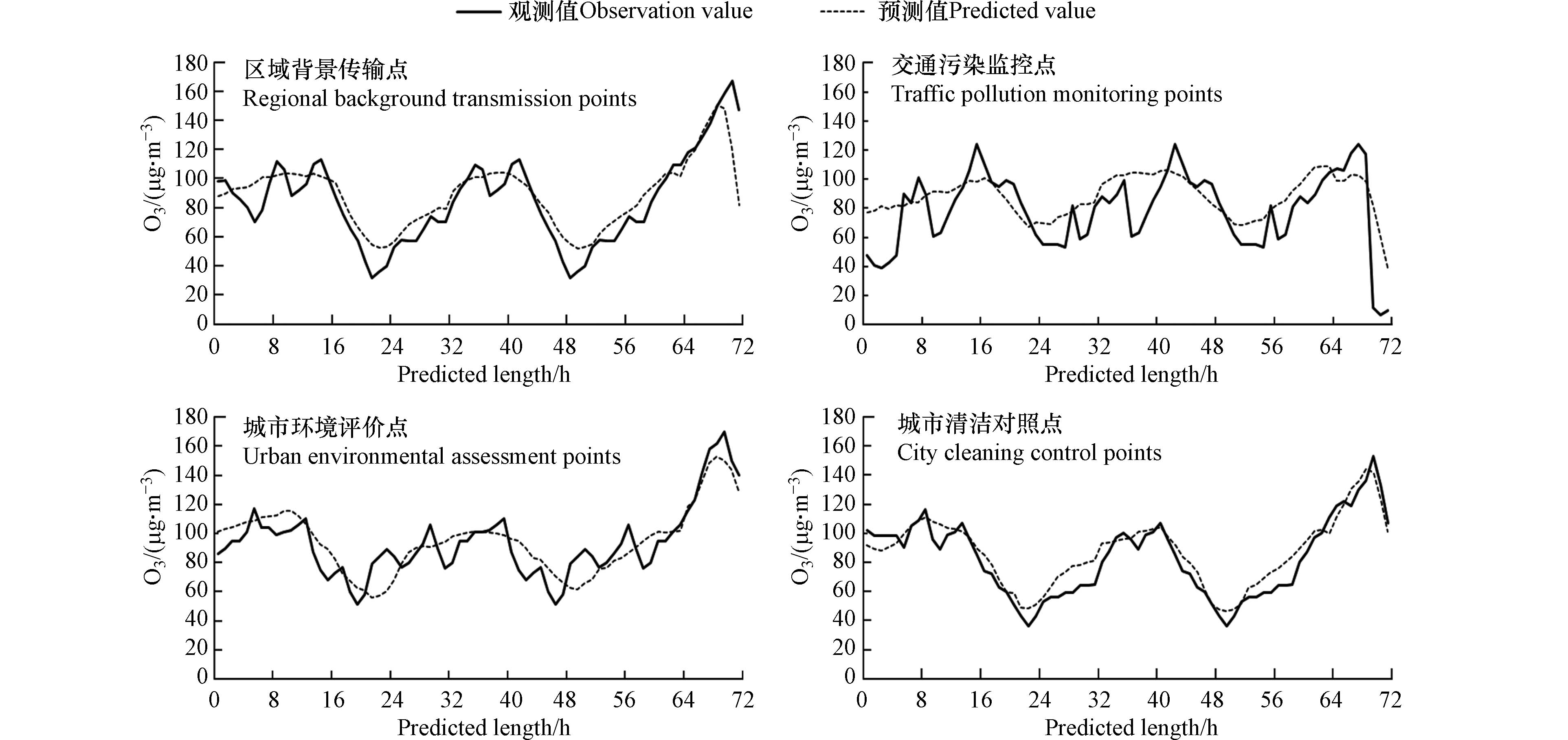
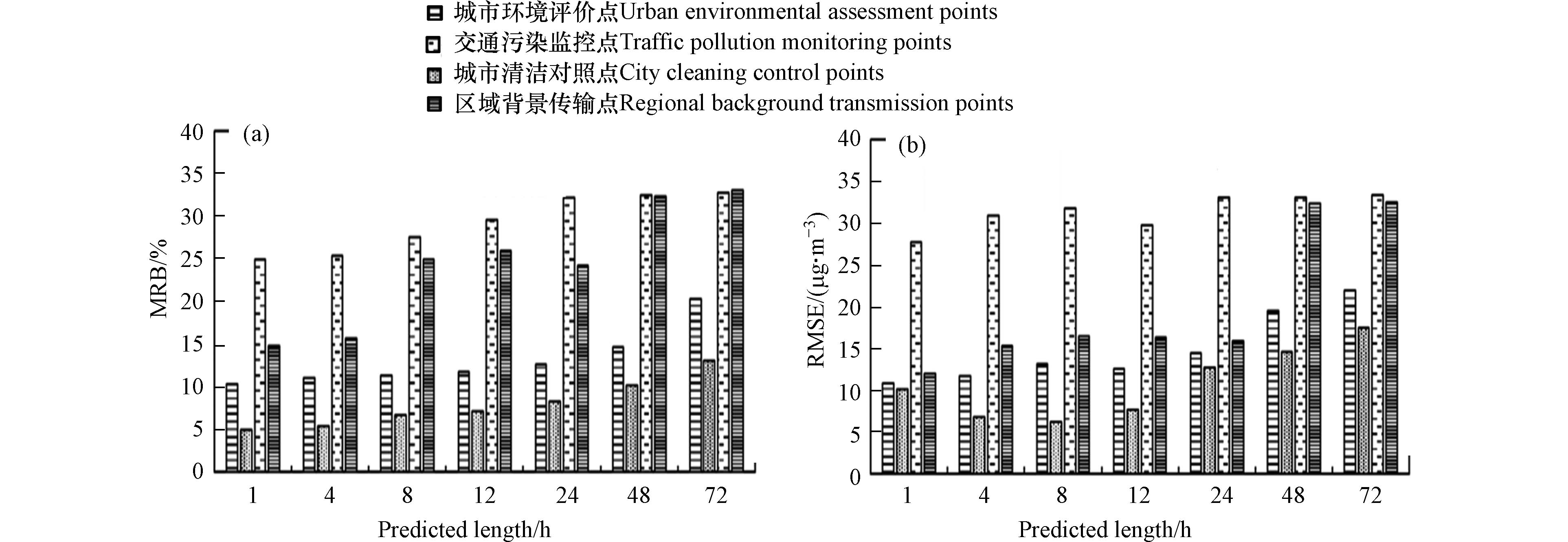
北京市共有35个空气质量监测站点, 包括23个城市环境评价点、1个城市清洁对照点、5个交通污染监控点和6个区域背景传输点, 分别用于评估城市不同功能区的空气质量状况与变化规律. 在四类站点中, 分别选取一个站点对比浓度预测值与观测值. 从图10可知, 模型对城市环境评价点及城市清洁对照点模型预测浓度值与观测浓度值拟合程度较好, 对区域背景传输点及交通污染监控点拟合程度相对较差.
进一步计算GCN-LSTM模型预测各类型站点不同时段臭氧浓度的误差, 如图11. 随着预测时长增加, 各类型站点预测误差均有所增加. 城市清洁对照点、城市环境评价点、区域背景传输点和交通污染监控点预测平均MRB值分别为7.9%、13.2%、24.4%和29.3%, RMSE值分别为10.8、14.9、20.1、31.4 μg·m−3. 相较于其他类型站点, 道路交通污染源所造成的臭氧前体物排放在时空上具有一定的不确定性, 交通污染监控点臭氧浓度变化规律更为复杂, 可能是导致交通污染监控点预测误差较大的原因之一. 利用主成分分析法(principal component analysis, PCA)对4种监测站点的六项大气污染物数据进行分析, 发现城市清洁对照点代表PM2.5、CO、NO2、PM10和SO2的因子得分均在0.75以上, 交通污染监控点、城市环境评价点和区域背景传输点各项因子得分差距较大, 表明这三类站点污染来源相对复杂, 导致模型未能准确提取数据特征, 致使这三类站点预测误差较大.
-
(1)图卷积神经网络(GCN)可捕捉城市大气臭氧浓度的空间传输特征, 将气象因子与臭氧空间传输特征输入长短期记忆神经网络(LSTM), 进一步捕捉时间依赖特征, 建立了基于深度学习的臭氧小时浓度预测模型GCN-LSTM.
(2)利用模型对北京市未来72 h臭氧浓度进行预测, 预测值与观测值决定系数R2为0.86, 模型可较好地预测出臭氧浓度的时间及空间分布特征. GCN-LSTM模型预测24、48、72 h臭氧浓度时, 平均相对偏差分别为18.2%、19.2%和22.9%, RMSE值为17.3、23.7、25.4 μg·m−3, 对于48 —72 h的长时浓度预测准确度优于已有机器学习模型.
(3)当臭氧观测浓度介于0—80 μg·m−3、80—160 μg·m−3和160—200 μg·m−3(共占总数据量的96.3%)时, 预测平均相对偏差分别为20.1%, 6.9%和16.4%;当臭氧浓度大于200 μg·m−3时, 模型预测平均相对偏差较大, 未来可增加拐点预测模块来减小预测误差.
(4)不同类型站点浓度预测时发现, 城市清洁对照点、城市环境评价点、区域背景传输点和交通污染监控点预测的平均相对偏差分别为7.9%、13.2%、24.4%和29.3%, RMSE值分别为10.8、14.9、20.1、31.4 μg·m−3, 模型对城市清洁对照点和城市环境评价点的预测准确度较高, 对区域背景传输点和交通污染监控点位预测时需考虑更多局域因素.
(5)使用本模型可较好预测城市大气臭氧小时浓度.
基于深度学习的城市臭氧小时浓度预测模型
Prediction model of urban ozone hourly concentration based on deep learning
-
摘要: 近地面高浓度臭氧(O3)对城市环境空气质量、植物生长和人体健康等均有较大影响. 因此,精准预报臭氧浓度对城市环境管理部门臭氧污染防治、居民出行决策建议、降低健康影响等具有重要意义. 深度学习模型对于非线性关系具有较强捕捉和学习能力,因此本研究提出一种基于深度学习算法的混合模型,利用图卷积神经网络(GCN)及长短期记忆神经网络(LSTM)分别捕捉臭氧浓度空间和时间变化特征,耦合气象因子,构建基于时空关联的臭氧小时浓度预测模型GCN-LSTM,并以北京市为例开展应用研究. 结果显示,GCN-LSTM模型可较好预测北京市未来72 h臭氧浓度,预测值与观测值决定系数为0.86;预测未来24、48、72 h臭氧浓度平均相对偏差分别为18.2%、19.2%和22.9%,RMSE值分别为17.3、23.7、25.4 μg·m−3,对于48 —72 h的长时预测准确度优于已有机器学习模型;当臭氧观测浓度介于0—80 μg·m−3、80—160 μg·m−3和160—200 μg·m−3时(共占总数据量的96.3%),预测平均相对偏差分别为20.1%、6.9%和16.4%;预测不同类型站点浓度时发现,城市清洁对照点、城市环境评价点、区域背景传输点和交通污染监控点的平均相对偏差分别为7.9%、13.2%、24.4%和29.3%,RMSE值分别为10.8、14.9、20.1、31.4 μg·m−3,模型对城市清洁对照点和城市环境评价点的预测准确度较高. 使用本模型对城市大气臭氧小时浓度预测,将较好助力城市大气臭氧污染防治工作.
-
关键词:
- O3 /
- 小时浓度预测 /
- 深度学习 /
- 图卷积神经网络 /
- 长短期记忆神经网络.
Abstract: High near-surface ozone concentrations (O3) have a significant impact on urban ambient air quality, plant growth and human health. Therefore, accurate forecasting of ozone concentrations is important for urban environmental management departments to prevent and control ozone pollution, advise residents on travel decisions, and reduce health impacts. Deep learning models have strong capturing and learning ability for nonlinear relationships. Therefore, this study proposes a hybrid model based on deep learning algorithm, using graph convolutional neural network (GCN) and long short-term memory neural network (LSTM) to capture the spatial and temporal variation of O3 concentration features respectively, coupled with meteorological factors, to build a GCN-LSTM based on spatio-temporal correlation of O3 hourly concentration prediction model, and to conduct an application study in Beijing. The results show that GCN-LSTM model can predict the future O3 concentration in Beijing for 72 hours with a correlation coefficient of 0.86 between the predicted and observed values; the mean relative bias (MRB) of the predicted future O3 concentrations for 24, 48 and 72 hours are 18.2%, 19.2% and 22.9%, with root mean square error (RMSE) values of 17.3, 23.7 and 25.4 μg·m−3 respectively; the prediction accuracy was better than that of the existing machine learning models for the long time of 48—72 h; when the observed O3 concentrations ranged from 0—80 μg·m−3, 80—160 μg·m−3 and 160—200 μg·m−3 (a total of 96.3% of the total data volume), the MRB were 20.1%, 6.9% and 16.4%, the RMSE were 10.8, 14.9, 20.1, 31.4 μg·m−3 respectively. The MRB of the predicted concentrations at different types of sites were found to be 7.9%, 13.2%, 24.4% and 29.3% for the urban clean control site, urban environmental assessment site, regional background transmission site and traffic pollution monitoring site, respectively, and model predicts urban clean control points and urban environmental assessment points with high accuracy. Using this model to predict the hourly O3 concentration in urban air will better help to prevent and control O3 pollution in urban air. -
-
-
[1] WANG M Y, YIM S H L, DONG G H, et al. Mapping ozone source-receptor relationship and apportioning the health impact in the Pearl River Delta region using adjoint sensitivity analysis [J]. Atmospheric Environment, 2020, 222: 117026. doi: 10.1016/j.atmosenv.2019.117026 [2] GUAN Y, XIAO Y, WANG F Y, et al. Health impacts attributable to ambient PM2.5 and ozone pollution in major Chinese cities at seasonal-level [J]. Journal of Cleaner Production, 2021, 311: 127510. doi: 10.1016/j.jclepro.2021.127510 [3] 董红召, 王乐恒, 唐伟, 等. 融合时空特征的PCA-PSO-SVM臭氧(O3)预测方法研究 [J]. 中国环境科学, 2021, 41(2): 596-605. DONG H Z, WANG L H, TANG W, et al. Research on PCA-PSO-SVM ozone prediction considering spatial-temporal features [J]. China Environmental Science, 2021, 41(2): 596-605(in Chinese).
[4] 李子凌. 基于时空数据的臭氧特征分析及其预测算法研究[D]. 北京: 北京交通大学, 2020. LI Z L. Research on ozone feature analysis and prediction algorithm based on spatio-temporal data[D]. Beijing: Beijing Jiaotong University, 2020(in Chinese).
[5] 肖德林, 邓仕槐, 邓小函, 等. 达州市城区环境空气质量变化趋势及CMAQ模型预报分析 [J]. 中国环境监测, 2021, 37(4): 92-103. XIAO D L, DENG S H, DENG X H, et al. Analysis of ambient air quality variation trend and CMAQ model forecast system in urban areas of Dazhou City [J]. Environmental Monitoring in China, 2021, 37(4): 92-103(in Chinese).
[6] RYU Y H, HODZIC A, DESCOMBES G, et al. Toward a better regional ozone forecast over CONUS using rapid data assimilation of clouds and meteorology in WRF-chem [J]. Journal of Geophysical Research:Atmospheres, 2019, 124(23): 13576-13592. doi: 10.1029/2019JD031232 [7] 周广强, 瞿元昊, 余钟奇. 长江三角洲城市臭氧数值预报与释用 [J]. 中国环境科学, 2021, 41(1): 28-36. ZHOU G Q, QU Y H, YU Z Q. Numerical forecast and improvement of ozone over YRD cities [J]. China Environmental Science, 2021, 41(1): 28-36(in Chinese).
[8] 邹国建. 基于时空特征学习的区域空气污染物扩散趋势预测研究[D]. 上海: 上海师范大学, 2020. ZOU G J. Study on prediction of regional air pollutant diffusion trend based on spatiotemporal feature learning[D]. Shanghai: Shanghai Normal University, 2020(in Chinese).
[9] 丁愫, 陈报章, 王瑾, 等. 基于决策树的统计预报模型在臭氧浓度时空分布预测中的应用研究 [J]. 环境科学学报, 2018, 38(8): 3229-3242. DING S, CHEN B Z, WANG J, et al. An applied research of decision-tree based statistical model in forecasting the spatial-temporal distribution of O3 [J]. Acta Scientiae Circumstantiae, 2018, 38(8): 3229-3242(in Chinese).
[10] 梁炜, 李雅箐, 黄喜寿, 等. 基于ARMA-GARCH模型的南宁市O3浓度预测研究 [J]. 广西科学, 2020, 27(1): 91-97. LIANG W, LI Y Q, HUANG X S, et al. Research on atmospheric ozone concentration prediction based on ARMA-GARCH model in Nanning [J]. Guangxi Sciences, 2020, 27(1): 91-97(in Chinese).
[11] 蔡旺华. 运用机器学习方法预测空气中臭氧浓度 [J]. 中国环境管理, 2018, 10(2): 78-84. CAI W H. Using machine learning method for predicting the concentration of ozone in the air [J]. Chinese Journal of Environmental Management, 2018, 10(2): 78-84(in Chinese).
[12] 彭岩, 冯婷婷, 王洁. 基于集成学习的O3的质量浓度预测模型 [J]. 山东大学学报(工学版), 2020, 50(4): 1-7. PENG Y, FENG T T, WANG J. An integrated learning approach for O3 mass concentration prediction model [J]. Journal of Shandong University (Engineering Science), 2020, 50(4): 1-7(in Chinese).
[13] 王舒扬, 姜金荣, 迟学斌, 等. 模式预报数据的深度学习PM2.5浓度预测模型[J]. 数值计算与计算机应用, 2022, 43(2): 142-153. WANG S Y, JIANG J R, CHI X B, et al. A deep learning model for forecasting PM2.5 combined with numerical model Data[J/OL]. Journal on Numerical Methods and Computer Application, 2022, 43(2): 142-153(in Chinese).
[14] SUN W, SUN J Y. Daily PM2.5 concentration prediction based on principal component analysis and LSSVM optimized by cuckoo search algorithm [J]. Journal of Environmental Management, 2017, 188: 144-152. [15] 宋国君, 国潇丹, 杨啸, 等. 沈阳市PM2.5浓度ARIMA-SVM组合预测研究 [J]. 中国环境科学, 2018, 38(11): 4031-4039. doi: 10.3969/j.issn.1000-6923.2018.11.005 SONG G J, GUO X D, YANG X, et al. ARIMA-SVM combination prediction of PM2.5 concentration in Shenyang [J]. China Environmental Science, 2018, 38(11): 4031-4039(in Chinese). doi: 10.3969/j.issn.1000-6923.2018.11.005
[16] 李建新, 刘小生, 刘静, 等. 基于MRMR-HK-SVM模型的PM2.5浓度预测 [J]. 中国环境科学, 2019, 39(6): 2304-2310. doi: 10.3969/j.issn.1000-6923.2019.06.009 LI J X, LIU X S, LIU J, et al. Prediction of PM2.5 concentration based on MRMR-HK-SVM model [J]. China Environmental Science, 2019, 39(6): 2304-2310(in Chinese). doi: 10.3969/j.issn.1000-6923.2019.06.009
[17] 康俊锋, 黄烈星, 张春艳, 等. 多机器学习模型下逐小时PM2.5预测及对比分析 [J]. 中国环境科学, 2020, 40(5): 1895-1905. doi: 10.3969/j.issn.1000-6923.2020.05.005 KANG J F, HUANG L X, ZHANG C Y, et al. Hourly PM2.5 prediction and its comparative analysis under multi-machine learning model [J]. China Environmental Science, 2020, 40(5): 1895-1905(in Chinese). doi: 10.3969/j.issn.1000-6923.2020.05.005
[18] ZENG Z L, WANG Z M, GUI K, et al. Daily global solar radiation in China estimated from high-density meteorological observations: A random forest model framework [J]. Earth and Space Science, 2020, 7(2): e2019EA001058. [19] 侯俊雄, 李琦, 朱亚杰, 等. 基于随机森林的PM2.5实时预报系统 [J]. 测绘科学, 2017, 42(1): 1-6. HOU J X, LI Q, ZHU Y J, et al. Real-time forecasting system of PM2.5 concentration based on spark framework and random forest model [J]. Science of Surveying and Mapping, 2017, 42(1): 1-6(in Chinese).
[20] HUANG K Y, XIAO Q Y, MENG X, et al. Predicting monthly high-resolution PM2.5 concentrations with random forest model in the North China Plain [J]. Environmental Pollution, 2018, 242: 675-683. doi: 10.1016/j.envpol.2018.07.016 [21] KAPADIA D, JARIWALA N. Prediction of tropospheric ozone using artificial neural network (ANN) and feature selection techniques [J]. Modeling Earth Systems and Environment, 2022, 8(2): 2183-2192. doi: 10.1007/s40808-021-01220-6 [22] KUMAR N, MIDDEY A, RAO P S. Prediction and examination of seasonal variation of ozone with meteorological parameter through artificial neural network at NEERI, Nagpur, India [J]. Urban Climate, 2017, 20: 148-167. doi: 10.1016/j.uclim.2017.04.003 [23] SAYEED A, CHOI Y, ESLAMI E, et al. Using a deep convolutional neural network to predict 2017 ozone concentrations, 24 hours in advance [J]. Neural Networks, 2020, 121: 396-408. doi: 10.1016/j.neunet.2019.09.033 [24] WANG H W, LI X B, WANG D S, et al. Regional prediction of ground-level ozone using a hybrid sequence-to-sequence deep learning approach [J]. Journal of Cleaner Production, 2020, 253: 119841. doi: 10.1016/j.jclepro.2019.119841 [25] 贾鹏程. 基于深度学习的长三角地区臭氧临近预报技术研究[D]. 南京: 南京信息工程大学, 2021. JIA P C. Deep learning based ozone prediction technique in Yangtze River Delta region[D]. Nanjing: Nanjing University of Information Science & Technology, 2021(in Chinese).
[26] 万显烈, 杨凤林, 王慧卿. 利用人工神经网络对空气中O3浓度进行预测 [J]. 中国环境科学, 2003, 23(1): 110-112. doi: 10.3321/j.issn:1000-6923.2003.01.025 WAN X L, YANG F L, WANG H Q. The approach of artificial neural network applied in ambient ozone forecast [J]. China Environmental Science, 2003, 23(1): 110-112(in Chinese). doi: 10.3321/j.issn:1000-6923.2003.01.025
[27] HOCHREITER S, SCHMIDHUBER J. Long short-term memory [J]. Neural Computation, 1997, 9(8): 1735-1780. doi: 10.1162/neco.1997.9.8.1735 [28] 周永生. 基于LSTM神经网络的PM2.5预测[D]. 长沙∶湖南大学, 2018. ZHOU Y S. PM2.5 Prediction based on LSTM neural network [D]. Changsha: Hunan University, 2018(in Chinese).
[29] AL-JANABI S, MOHAMMAD M, AL-SULTAN A. A new method for prediction of air pollution based on intelligent computation [J]. Soft Computing, 2020, 24(1): 661-680. doi: 10.1007/s00500-019-04495-1 [30] FREEMAN B S, TAYLOR G, GHARABAGHI B, et al. Forecasting air quality time series using deep learning [J]. Journal of the Air & Waste Management Association, 2018, 68(8): 866-886. [31] JIA P C, CAO N W, YANG S B. Real-time hourly ozone prediction system for Yangtze River Delta area using attention based on a sequence to sequence model [J]. Atmospheric Environment, 2021, 244: 117917. doi: 10.1016/j.atmosenv.2020.117917 [32] PAK U, KIM C, RYU U, et al. A hybrid model based on convolutional neural networks and long short-term memory for ozone concentration prediction [J]. Air Quality, Atmosphere & Health, 2018, 11(8): 883-895. [33] 方韬. 基于神经网络的近地面臭氧估算和预测研究[D]. 上海: 上海师范大学, 2020. FANG T. Study on estimation and prediction of near-surface ozone based on neural network[D]. Shanghai: Shanghai Normal University, 2020(in Chinese).
[34] ZHOU J, CUI G Q, HU S D, et al. Graph neural networks: A review of methods and applications [J]. AI Open, 2020, 1: 57-81. doi: 10.1016/j.aiopen.2021.01.001 [35] RESHEF D N, RESHEF Y A, FINUCANE H K, et al. Detecting novel associations in large data sets [J]. Science, 2011, 334(6062): 1518-1524. doi: 10.1126/science.1205438 [36] 高婵娟, 赵啟超, 丁若男, 等. 2018年吉林市大气污染物浓度变化及其与气象因素的相关性分析 [J]. 环境工程, 2021, 39(5): 71-79. GAO C J, ZHAO Q C, DING R N, et al. Variations of atmospheric pollutants concentrations and their correlation with meteorological factor in Jilin City in 2018 [J]. Environmental Engineering, 2021, 39(5): 71-79(in Chinese).
[37] ZHENG Y, YI X W, LI M, et al. Forecasting fine-grained air quality based on big data[C]//Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Sydney NSW Australia. New York, NY, USA: ACM, 2015: 2267-2276. -


 下载:
下载: