-
污泥是生活污水经过沉降脱水产生的固体废物，污泥中含有寄生虫卵、病原微生物等致病物质，铜、锌、铬等重金属，这些污染物相互连接又被细菌包裹形成胞外聚合物[1]，导致污泥锁住水分，此外，污泥还含有多氯联苯、二噁英等难降解有毒有害物质[2]，如果不妥善处理，容易造成二次污染。随着城镇化进程加快，到2025年前后，我国大中型城市污泥处置率将达到95%以上[3]。污泥最显著的特征是含水率高，即使经过浓缩与消化后，污泥的含水率仍然在95%以上，机械脱水后含水率降低至85%左右[3]。污泥中大部分水分仅靠外力挤压很难被脱除，胞外聚合物的存在阻碍着这部分水分的释放。污泥焚烧是污泥减容、减量、无害化处理的重要手段，但在此之前，仍需要依靠热能将污泥含水率干燥至65%以下才可实现自持燃烧。
污泥具有含水率高、粘性大、待处理量大等特点，超声波特别适合预处理这类物质，尤其是在热对流温度较低时，超声波可以在不显著加热污泥的情况下利用声流、海绵效应和空化效应，使其固液分离并减少传质的内部阻力，提高干燥速率[4-5]。SUN等[6]发现适宜的超声波可明显改善污泥的脱水性，赵芳等[7]分析讨论了超声声能密度、超声热效应等因素对污泥干燥过程的影响，证明超声作用可以加速污泥干燥速率，且超声强化效果随着声能密度的增加逐渐增强。在目前超声波处理污泥的研究多集中于以下方面，其一是污泥沉降方面，考察超声波对污泥沉降速率以及对厌氧消化过程的酶活性、脱氮速率、胞外聚合物产生影响[8]，其二是超声波直接与热载体进行联合干燥，分析对比薄层污泥厚度以及超声波功率对干燥过程的影响[9-10]，但对经过超声波预处理污泥的干燥过程鲜有研究。
本研究的目的是通过热对流干燥实验，通过控制超声波频率和预处理时间，分析超声波预处理对污泥含水量以及干燥速率的影响。考虑到实际生产的目标水分与最佳掺烧含水率，本研究以全干化 (含水率小于5%) 为干燥目标。同时，使用Origin软件建立了超声波预处理后的污泥热湿耦合模型，通过干燥动力学研究污泥干燥过程中水分比与各个因素之间的关系，从宏观和微观2个层面间接描述传热传质的变化规律。
-
污泥样品来自沈阳市铁西区污水处理厂经过机械脱水后的污泥，污泥呈黑色泥膏状，气味强烈，静置48 h后下层污泥渗出污水，上层表面出现白色霉菌，恶臭气味更加强烈，样品初始含水率为84.96%。
-
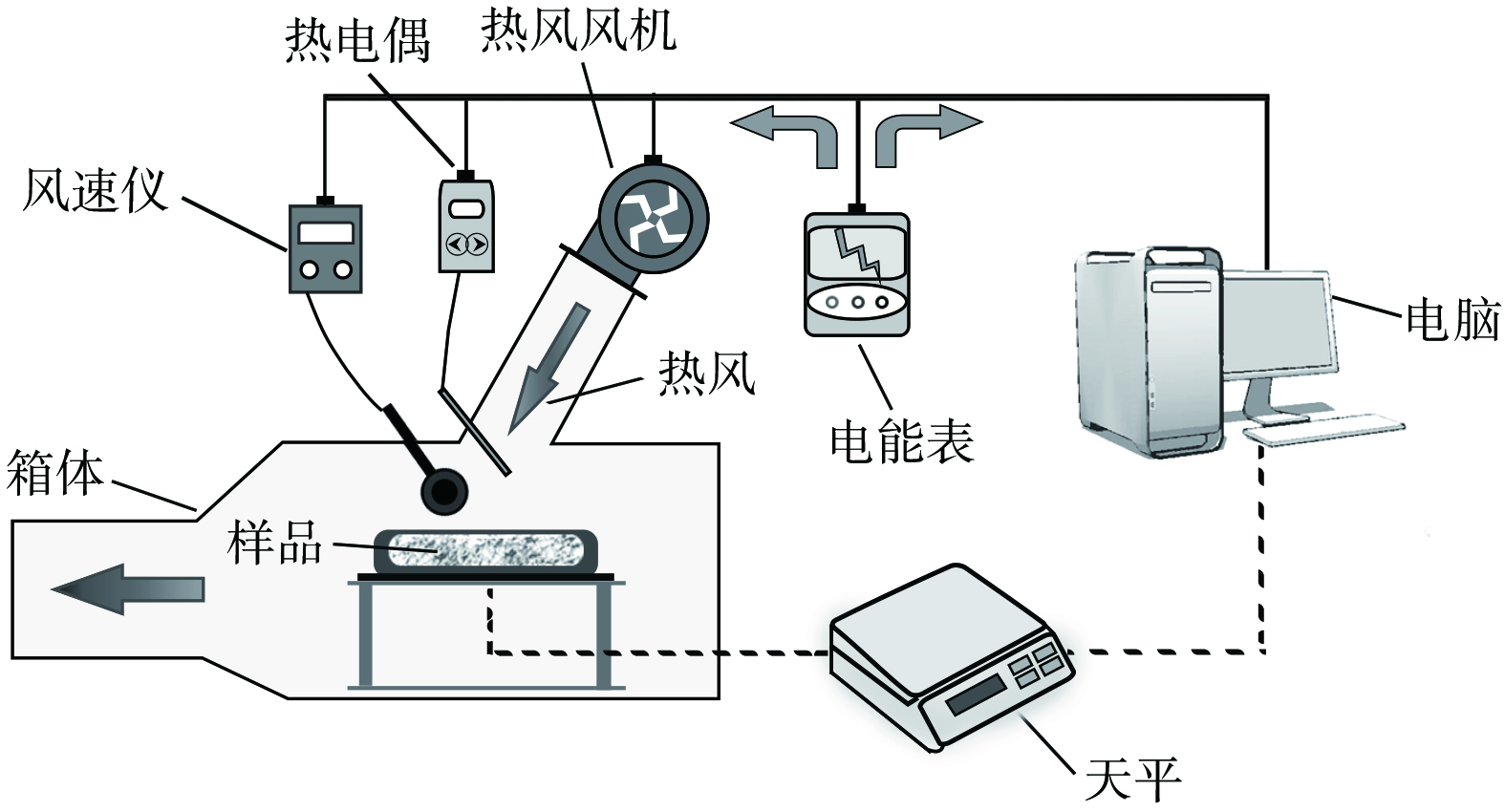
污泥热对流干燥器装置如图1 所示，装置包括密封干燥箱体、无极调温风机、数据采集器组成。其中包括：分析天平 (JE2003，上海尚普仪器设备有限公司) ；工业热风机 (DL5318，得力工具有限公司) ；风速仪 (DL333212，得力工具有限公司) ；超声波发生器 (THD-T1，深圳太和达科技有限公司) ；超声波换能器 (THD-T1，深圳太和达科技有限公司) 。
-
试验开始前先将污泥置于超声波振板上预处理至预设时间，再放入污泥热对流干燥装置中。试验所用的调温风机60~590 ℃连续可调，通过风口调节器调节风速。托盘中将污泥铺成10 cm×10 cm厚度6 mm方形薄片。试验开始前，先将风速仪从干燥箱体预留的小孔伸入，调节风速为2 m·s−1，再将K形热电偶伸入，调节温度到达指定温度进行预热，最后将污泥置于天平托盘，关闭热风箱体门进行热对流干燥试验。数据采集器记录分析天平的实时数据，通过连接电脑实现数据的保存、显示和实时计算。
其超声波预处理系统设置功率为30 W，超声波频率选取25与40 kHz 2个频率等级，分别处理2和4 h。干燥箱内设置70、90、110、130 ℃的4个干燥温度。若连续3次干燥速率小于5.0×10−4 s−1则认为干燥过程结束，并记录电能表示数。每组试验进行3次以确保再现。
-
薄层干燥模型常用于描述污泥水分的质量损失，表1列出了7种常用的薄层干燥模型。利用决定系数R2、卡方系数χ2、平均根误差RMSE可以衡量模型拟合效果，讨论最佳模型。R2值越高、χ2与RMSE值越低代表拟合效果越好，干燥模型就越合适。
-
水分比 (MR) 与干燥速率 (DR) 的公式分别为式(1)、(2)和式(3)。
式中：M0是样品未干燥状态的干基含水率；Mt是样品干燥到任意时刻的干基含水率；Me是样品干燥到平衡状态的干基含水率。
由于污泥样品干燥到平衡状态时Me远小于M0、Mt，所以式(1)可以简化为(2)。
有效湿分扩散系数表明了液态水或气态水利用样品裂缝、空隙和微通道的扩散效率。有效湿分扩散系数受污泥样品特性、水分含量、热对流温度和速度以及超声功率和频率等因素影响，是衡量干燥过程的关键指标。在超声波强化热对流干燥的过程中干燥时间足够长，为了方便计算需要对干燥过程进行如下假设：水分迁移是通过自由扩散且不考虑径向扩散，具有恒定的有效湿分扩散系数与干燥温度，水分由薄层底面扩散至蒸发面[11]。则薄层污泥样品可用Fick第二定律的对数形式表示，如式(4)所示。
式中：MR是水分比，Deff是有效湿分扩散系数，m2·s−1；L是薄层污泥厚度，m；t是干燥所用的时间，s。
式(4)成立的是以Deff是个定值为前提条件，但大量实验证明有效湿分扩散系数的值随着水分含量的减少而增加[12]。傅里叶数的物理意义为非稳态传质传热过程，将傅里叶数公式F0=Defft/L2带入式(4)计算得到式(5)[13]。
那么有效湿分扩散系数计算式可整理为式(6)。
在此lnMR与Deff呈函数关系，此函数关系表示为F(lnMR)，Deff的估计值受到实验和分析处理误差的制约，估算每个干燥温度下的某段有效湿分扩散系数的平均值则应用式(7)进行积分[14]。
扩散过程的表观活化能由式(8)Arrhenius方程的对数形式来确定[15]，lnDeff与试验热对流温度T呈函数关系，Ea可通过直线斜率求得。
式中：D0是扩散因子，m2·s−1；Ea是表观活化能，kJ/mol；T是试验热风温度，K；R通用气体常数，8.314 J·(mol·K)−1。
-
图2给出不同超声波频率、预处理时间、热对流温度下的污泥水分比曲线和干燥速率曲线，可以看出污泥的干燥结束时间随着热对流温度的提高而逐渐缩短。以无预处理的污泥为例，干燥用时分别为：70 ℃用时9 471 s、90 ℃用时8 181 s、110 ℃用时7 004 s、130 ℃用时6 712 s。比较图2还可以看出超声波预处理对各个温度环境下的污泥样品的干燥效果均有强化作用，随着预处理时间增加，这种强化作用也更加明显，详细干燥用时缩短的百分比数据已总结在表2。
可见超声波预处理对污泥的干燥具有促进作用，这是由于污泥中自由水占66%~86%，污泥中含有大量有机分子、无机颗粒和细菌真菌胶质体，水的极性分子与细菌真菌胶质体的极性分子形成氢键，产生较强的吸附力，导致污泥集团吸附自由水[16]。由于超声波在胶质体中作用效果良好，超声波的强剪切力破碎分离了污泥集团[7]，释放了被聚合物基团锁住的自由水，故而产生了这种强化作用。与此同时，基团碎片体积缩小并相互聚合，在污泥内部形成微通道，有利于污泥内部水分向表面扩散。实验发现经过25 kHz的超声波预处理的污泥干燥时间更短，这可能由于不同频率的超声波在污泥中的特性阻抗不同，更低的超声波频率衰减系数更小[17]，因此在相同预处理时间下，经过25 kHz的超声波频率预处理的污泥干燥时间更短。
通过干燥速率曲线得知，热对流薄层污泥干燥过程可分为：预热阶段、恒速干燥阶段、第一降速干燥阶段、第二降速干燥阶段[10]。超声波预处理明显提高恒速干燥阶段(含水率75%~40%)的干燥速率，且热对流温度越高干燥速率提升就越明显，详细干燥速率数据总结在表2。
由表2可以看出经过超声波预处理的污泥在110和130 ℃热对流温度下的恒速干燥速率明显提升，这是由于较高的热对流温度使污泥内部水分沸腾，提高了内部水汽压力，从而将自由水推动到污泥表面，而超声波的强剪切力形成的局部拉应力足以克服液体分子的结合力造成聚合物基团内部产生负压空洞，形成空穴[18]，在压力与空穴的双重影响下不连续的气相和液相推动水分扩散，促使水分通过自然通道迁移排出，所以在较高的热对流温度下干燥速率提升明显。值得一提的是恒速干燥阶段结束时污泥的含水率可以满足绝大部分的工业干燥的水分目标[2-4]，这意味着超声波预处理技术可以得到广泛的利用。
随着干燥的继续，含水率降低到40%以下时进入第一降速阶段，此阶段裂纹不再发展延伸，薄层污泥收缩成2~4个部分，污泥出现了表面结壳但内部还是湿污泥的现象，这增大了传质阻力，阻碍内部的水分往外界扩散。当水分比下降至0.1左右时，干燥速率曲线的继续斜率增大，干燥过程进入第二降速干燥阶段，这一阶段大部分自由水和部分毛细结合水已经脱除，剩余少量的毛细结合水和微量的表面吸附水，这部分水与污泥结合更加紧密，需要更多能量才能除去。
-
在7种干燥模型中，Midilli模型R2的平均值为0.999 3，Modified模型R2的平均值为0.998 7，Midilli模型与Modified模型均有较好的R2值，同时Midilli模型χ2均值 (1.224×10−4) 与RMSE均值 (8.635×10−3) 均低于其他模型，因此Midilli模型能更好的表达干燥过程中污泥含水率与时间的关系，Midilli模型拟合结果详见表3。
从表3中可以观察出，超声波频率、预处理时间和热对流温度的变化对拟合系数k的影响较大，对模型系数n的影响较小，模型系数a和b则不受超声波频率、预处理时间和热对流温度变化的影响，属于模型的修正系数。为了验证Midilli模型在不同环境下干燥的描述的准确性，将试验过程中各个实验条件的水分比与模拟值进行对比，如图3所示，明显可以看出所有的实验数据与模拟值形成一条斜率为1的直线，实验值与拟合值的决定系数R2为0.999 7，再次显示了Midilli模型在不同实验条件下描述干燥动力学的适用性。
-
干燥动力学的参数可以更好的描述污泥样品的干燥行为，图4给出式6中F(lnMR)与t的关系图象，其斜率变化反映了效湿分扩散系数Deff的变化。从图4中观察到函数斜率并非恒定不变，Deff的值明显随着水分含量的减少而增加，当达到干燥过程的最后阶段时，Deff的值几乎以指数趋势增长。
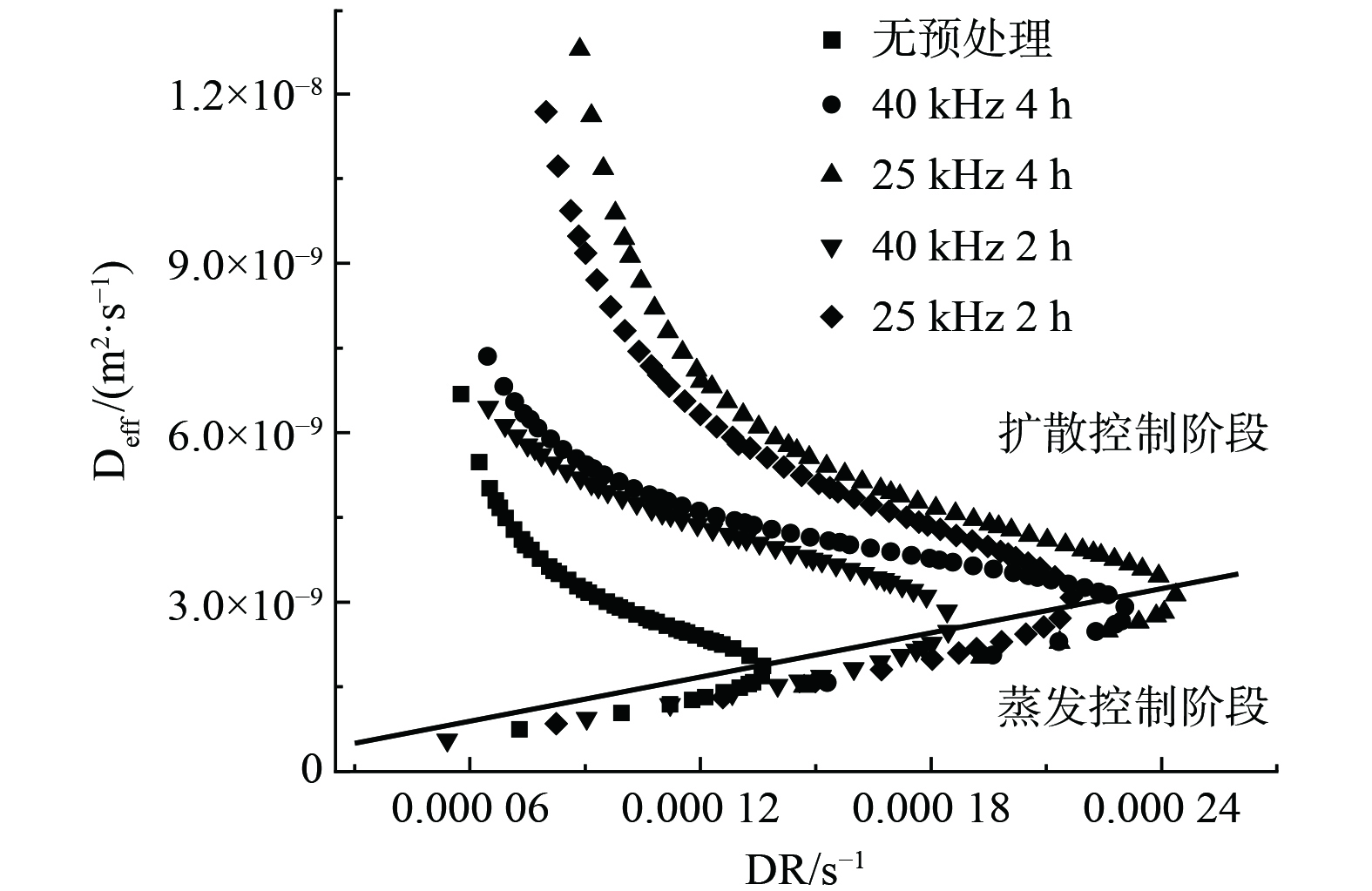
由图5可见，污泥的干燥可划分为2个阶段：蒸发控制阶段和扩散控制阶段。蒸发控制阶段：支配水分运输的物理过程是蒸发，在干燥初期，样品表面有大量水分存在，在污泥的结构之间孔隙中的游离水从样品中心转移到表面，而蒸发在样品表面附近发生[19]；扩散控制阶段：当大部分游离水从表面中脱除，热量逐渐传递至污泥内部，水分慢慢从内部扩散至表面产生浓度梯度，这个过程中支配水分传输的物理过程是扩散，在这期间样品表层结构中的孔隙由于其内部水蒸气压力的增加而变宽[10]，直至干燥末期。通过式(7)可以得到不同条件下2阶段的Deff的值，其结果详见表4。可见在一定的超声功率下，污泥在2个阶段的有效湿分扩散系数随着干燥温度的升高和预处理时间增加而增大，其中在频率25 kHz预处理4 h的条件下Deff值增幅最大，由1.23×10−9 m2·s−1增加到3.99×10−9 m2·s−1。
根据表4数据可对lnDeff与T−1进行拟合并通过式(8)求得表观活化能，图6给出的是在超声波频率25 kHz预处理4 h 条件下的不同阶段lnDeff与T−1拟合情况。表观活化能的值可以表示从样品中除去水分所需的最小能量值，用来衡量干燥过程的难易程度，表观活化能Ea的值越小干燥就越容易[20]。由表5中数据可以计算出，经过预处理的污泥蒸发控制阶段和扩散控制阶段Ea的平均值分别为21.45 kJ·mol−1和22.02 kJ·mol−1，蒸发控制阶段的Ea略低于扩散控制阶段的Ea。与未预处理的样品相比，预处理过的2个段干燥过程的Ea都有降低，以经过超声波25 kHz预处理2 h的污泥为例，2个阶段Ea分别为20.86 kJ·mol−1和20.95 kJ·mol−1，减少了19.34%和22.21%。另外，表5还表明更长时间的预处理并没有降低Ea的值，但大幅增加了扩散因子D0值，还是以25 kHz超声波为例，污泥的预处理时长由2 h增加至4 h，蒸发控制阶段的D0从1.33×10−6 m2·s−1增加至3.42×10−6 m2·s−1，扩散控制阶段的D0从2.22×10−6 m2·s−1增加至6.55×10−6 m2·s−1。这也证明了超声波预处理对水分扩散有积极作用，而且预处理时间越长这种作用就越明显。
根据表5还可知，相同预处理时间下，不同频率超声波进行预处理的污泥表观活化能Ea差异较小，差异在0.91%~7.96%之间，但使用25 kHz超声波进行预处理会使干燥过程具有更高的扩散因子D0，经过25 kHz超声波预处理的污泥2个阶段的D0平均值分别为2.37×10−6 m2·s−1和3.08×10−6 m2·s−1，而经过40 kHz超声波的污泥2个阶段D0平均值分别为1.98×10−6 m2·s−1和2.36×10−6 m2·s−1。由此可以看出使用25 kHz超声波预处理对污泥水分扩散作用更加明显。
-
为探究超声波预处理对污泥孔隙率的影响，本研究对不同预处理条件下干燥完成的干污泥进行孔隙率检测。检测干燥终点原始污泥的平均孔隙率为37.21%，在不同的干燥条件下，污泥的平均孔隙率如下：经过25 kHz 2 h预处理污泥平均孔隙率43.36%、经过25 kHz 4 h预处理污泥平均孔隙率49.27%、经过40 kHz 2 h预处理污泥平均孔隙率41.15%、经过40 kHz 4 h预处理污泥平均孔隙率47.57%。超声波预处理使污泥的孔隙率增加，并且预处理时间和超声波频率对孔隙率都有影响。其中，经过25 kHz 4h预处理的污泥，孔隙率提升幅度最高，为13.06%。由于污泥是非牛顿假塑性流体，更低的振动频率意味着更高的单次剪切强度，可以改变污泥的触变性与粘弹性[21-22]，另外相关研究也指出更低的超声波的频率更能影响样品孔隙形变的分布趋势和形变大小[23]。
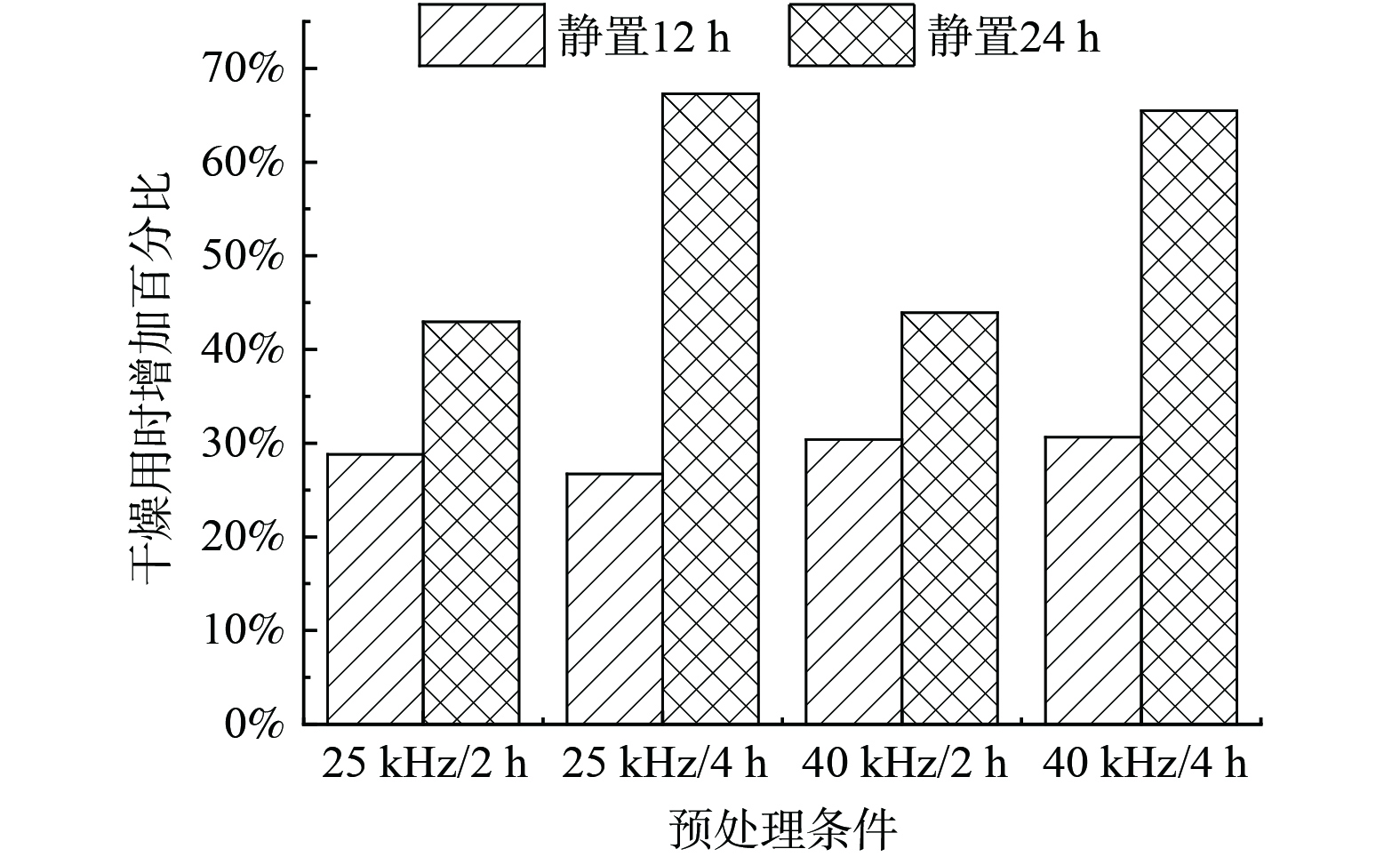
水分复吸特性是指预处理后的污泥放置一段时间后，污泥的干燥速率逐渐趋近于未处理的状态，图7展示了污泥的复吸状况。从图7中可以看出，预处理污泥静置12 h后，各组的复吸程度差别不大，都在26%~31%之间。然而静置24 h后，经过4 h预处理的污泥的复吸水平明显高于其他2组。为探究复吸的原因，对4种预处理渗出液的COD浓度进行了分析。结果显示，经过25 kHz 2 h预处理污泥的COD浓度为67.54 mg·L−1，经过25 kHz 4 h预处理污泥的COD浓度为73.64 mg·L−1，经过40 kHz 2 h预处理污泥的COD浓度为65.95 mg·L−1，经过40 kHz 4 h预处理污泥的COD浓度为71.33 mg·L−1。这表明在预处理4 h的情况下，污泥的细胞结构被破坏得更多，导致污泥中存在更多的有机质，这些有机质使微生物在污泥中生长，将已经释放的水分再次包裹进去，从而影响了干燥的时长。
-
1) 超声波预处理显著加快了污泥干燥速度，尤其是在热对流温度越高的情况下，这种强化效果尤为明显。超声波的强剪切力可以破碎污泥集团释自由水，其中25 kHz超声波具有较高的干燥速率提升。Midilli模型能更好的表达各个预处理条件污泥干燥时含水率与时间的关系。
2) 通过计算表明有效湿分扩散系数随着水分比的减小缓慢增加，干燥后期接近于指数增长。污泥的干燥过程可以分为蒸发控制阶段和扩散控制阶段，预处理可以显著增加这2个阶段的有Deff值，使用25 kHz超声波进行预处理使干燥过程Deff的值更高，并且增加预处理时间也可大幅增加Deff值。
3) 蒸发控制阶段的表观活化能略低于扩散控制阶段的表观活化能，而更长的预处理时间并没有使表观活化能减小，超声波频率变化对表观活化能的影响较小，但25 kHz超声波预处理的污泥的扩散因子更高。
4) 干燥结束后，预处理的污泥孔隙率高于原污泥，25 kHz超声波预处理4 h可以使孔隙率提高13.06%。过长的预处理时间会导致污泥内部有机质增加，导致微生物的繁殖使干燥时间延长。在本文试验条件中，使用25 kHz超声波进行2 h的预处理组合是较为合理的选择。
超声波预处理对污泥热对流干燥影响及热力学分析
Ultrasonic pretreatment on the influence of sludge convective drying and thermodynamic analysis
-
摘要: 为了探究经过超声波预处理的污泥在热对流中的干燥效果，选用了频率为25和40 kHz的超声波，分别对污泥进行2 和4 h的预处理，完成预处理的污泥在70、90、110、130 ℃下进行热对流干燥，并对实验数据进行数学拟合。结果表明，超声波预处理可以有效提升污泥的干燥速率，在整个干燥温度范围内，经过25 kHz的超声波预处理的污泥干燥速率更快，预处理时间2和4 h分别使干燥时间缩短了23.19%和29.15%，且热对流温度越高干燥时间就越短；在7种干燥模型中，Midilli模型更能精确表达预处理后污泥的薄层干燥行为。根据傅里叶变换的Fick第二定律表达式显示出Deff呈现指数增长，25 kHz的超声波对污泥Deff的提升要优于40 kHz，经过不同超声波预处理的污泥表观活化能Ea差异较小，但是25 kHz超声波使污泥具有更高的扩散因子D0，约为3.146×10−6 m2·s−1。此外，超声预处理时间不宜过长，否则会导致复吸现象加剧。Abstract: In order to investigate the drying effect of sludge after ultrasound pretreatment in convective drying, ultrasound with frequencies of 25 kHz and 40 kHz was used to pretreat the sludge for 2 and 4 h, respectively. The pretreated sludge was then subjected to convective drying at 70, 90, 110, and 130 ℃, and the experimental data was mathematically fitted. The results showed that ultrasound pretreatment can effectively increase the drying rate of the sludge. Within the entire drying temperature range, the sludge pretreated with 25 kHz ultrasound had a faster drying rate, with pretreatment times of 2 and 4 h reducing the drying time by 23.19% and 29.15%, respectively. This improvement was more significant at higher convective drying temperatures. Among the seven drying models, the Midilli model more accurately represented the behavior of the pretreated thin-layer drying. According to the Fourier transform of the Fick's second law, Deff exhibited exponential growth, and the increase in Deff for sludge treated with 25 kHz ultrasound was better than that for 40 kHz. The difference in apparent activation energy Ea of sludge pretreated with different ultrasound is small, but the 25 kHz ultrasound resulted in a higher D0 for the sludge, approximately 3.146×10−6 m2·s−1. In addition, the ultrasound pretreatment time should not be too long, as it may lead to an exacerbation of reabsorption phenomenon.
-
Key words:
- ultrasonic waves /
- domestic /
- drying /
- thermal effect
-
-
图 2 不同预处理条件下含水率和干燥速率随温度的变化
Figure 2. Variation of moisture content and drying rate with temperature under different pretreatment conditions
图 3 MR实验值与Midilli模型的模拟值的关系
Figure 3. Relationship between experimental MR values and simulated MR values of Midilli model
图 5 有效湿分扩散系数与干燥速率关系
Figure 5. Relationship between effective moisture diffusion coefficient and drying rate ‘
图 7 静置不同时长污泥在90 ℃下干燥用时增加百分比%
Figure 7. Percentage increase in drying time of sludge at 90 °C with different settling times
表 1 薄层干燥模型
Table 1. Thin-layer drying models
序号 理论模型 表达式 1 Lewis MR=exp(−kt) 2 Page MR=exp(−ktn) 3 Modified MR=exp(−(kt)n) 4 Henderson and Pabis MR=aexp(−kt) 5 Logarithmic MR=aexp(−kt)+c 6 Wang and Singh MR=1+at+bt2 7 Midilli MR=aexp(−ktn)+bt 
下载: 导出CSV
表 2 不同条件下恒速干燥阶段水分比范围和干燥速率
Table 2. Moisture content range and drying rate during constant-speed drying stage under different conditions
热对流温度 预处理条件 水分比 用时缩短百分比/% 干燥速率/s−1 热对流温度 预处理条件 预处理水分比 用时缩短百分比/% 干燥速率/s−1 70 ℃ 无预处理 0.82~0.47 — 1.10×10−4 90 ℃ 无预处理 0.85~0.45 — 12.8×10−4 25 kHz 2 h 0.84~0.46 10.76 1.38×10−4 25 kHz 2 h 0.83~0.45 11.06 1.46×10−4 25 kHz 4 h 0.84~0.45 12.05 1.64×10−4 25 kHz 4 h 0.82~0.38 14.93 1.47×10−4 40 kHz 2 h 0.84~0.47 9.26 1.27×10−4 40 kHz 2 h 0.83~0.42 10.25 1.38×10−4 40 kHz 4 h 0.85~0.47 11.77 1.26×10−4 40 kHz 4 h 0.83~0.41 13.65 1.43×10−4 110 ℃ 无预处理 0.84~0.41 — 1.62×10−4 130 ℃ 无预处理 0.80~0.37 — 1.81×10−4 25 kHz 2 h 0.84~0.42 14.65 1.92×10−4 25 kHz 2 h 0.87~0.32 21.07 2.03×10−4 25 kHz 4 h 0.86~0.44 21.10 2.22×10−4 25 kHz 4 h 0.83~0.33 28.58 3.67×10−4 40 kHz 2 h 0.81~0.34 11.65 1.65×10−4 40 kHz 2 h 0.82~0.31 15.11 1.91×10−4 40 kHz 4 h 0.86~0.45 19.71 2.13×10−4 40 kHz 4 h 0.86~0.30 24.89 2.55×10−4
下载: 导出CSV
表 3 Midilli模型拟合结果
Table 3. Statistical results for Midilli models
预处理条件 热对流温度 模型参数 R2 χ2 RMSE 无预处理 70 ℃ a=0.989 3, n=1.470 8, k=2.724 1×10−6, b=−2.944 1×10−6 0.999 3 8.417×10−5 0.009 2 90 ℃ a=0.980 9, n=1.422 4, k=5.734 5×10−6, b=−2.169 9×10−7 0.998 7 1.61×10−4 0.012 7 110 ℃ a=0.986 5, n=1.464 0, k=5.056 7×10−6, b=−9.256 0×10−6 0.998 9 1.665×10−4 0.012 9 130 ℃ a=0.990 6, n=1.536 4, k=2.825 4×10−6, b=−1.480 2×10−6 0.9994 8.054×10−5 0.009 0 25 kHz 2 h 70 ℃ a=0.993 3, n=1.284 0, k=1.522 9×10−5, b=−1.068 5×10−5 0.999 7 3.870×10−5 0.006 2 90 ℃ a=0.989 1, n=1.389 7, k=7.725 6×10−6, b=−8.761 3×10−6 0.999 3 8.640×10−5 0.009 3 110 ℃ a=0.989 0, n=1.401 1, k=1.066 7×10−5, b=−1.218 2×10−5 0.998 9 1.718×10−4 0.013 1 130 ℃ a=0.994 0, n=1.477 6, k=7.396 3×10−6, b=−1.119 3×10−5 0.999 7 4.644×10−5 0.006 8 25 kHz 4 h 70 ℃ a=0.998 9, n=1.161 0, k=4.165 1×10−5, b=−8.062 2×10−6 0.999 9 8.12×10−6 0.002 9 90 ℃ a=0.991 1, n=1.313 4, k=1.260 4×10−5, b=−1.461 1×10−5 0.999 1 1.152×10−4 0.010 7 110 ℃ a=0.983 8, n=1.472 6, k=5.066 7×10−6, b=−1.153 6×10−5 0.997 7 3.429×10−4 0.018 5 130 ℃ a=0.992 3, n=1.387 4, k=1.027 9×10−5, b=−2.006 5×10−5 0.999 0 1.599×10−4 0.012 6 40 kHz 2 h 70 ℃ a=0.990 0, n=1.320 3, k=1.141 3×10−5, b=−6.213 0×10−6 0.999 5 5.992×10−5 0.007 7 90 ℃ a=0.987 0, n=1.405 1, k=6.157 0×10−6, b=−1.501 3×10−5 0.998 9 1.503×10−4 0.012 3 110 ℃ a=0.996 5, n=1.203 9, k=5.673 5×10−5, b=−9.024 6×10−6 0.999 7 4.052×10−5 0.006 4 130 ℃ a=0.998 1, n=1.232 7, k=5.172 3×10−5, b=−2.148 9×10−5 0.999 4 1.094×10−4 0.010 5 40 kHz 4 h 70 ℃ a=0.998 9, n=1.161 0, k=4.165 1×10−5, b=−8.062 2×10−6 0.999 9 8.122×10−6 0.002 9 90 ℃ a=0.991 0, n=1.313 4, k=1.260 4×10−5, b=−1.461 1×10−5 0.999 1 1.152×10−4 0.010 7 110 ℃ a=0.983 8, n=1.472 6, k=5.066 7×10−6, b=−1.153 6×10−5 0.997 7 3.429×10−4 0.018 5 130 ℃ a=0.992 6, n=1.387 4, k=1.027 9×10−5, b=−2.006 5×10−5 0.999 0 1.599×10−4 0.012 6
下载: 导出CSV
表 4 不同超声波预处理条件下污泥的有效湿分扩散系数
Table 4. Effective moisture diffusivities of sewage sludge during ultrasonic-assisted convective thin-layer drying
预处理条件 热对流
温度/℃蒸发控制阶段 扩散控制阶段 Deff/ (m2·s−1) R2 Deff/ ( m2·s−1) R2 无预处理 70 1.32×10−9 0.999 9 8.85×10−10 0.999 7 90 1.49×10−9 0.999 3 1.15×10−9 0.999 6 110 1.68×10−9 0.998 9 1.29×10−9 0.999 0 130 1.89×10−9 0.999 8 1.59×10−9 0.990 5 25 kHz 2 h 70 1.33×10−9 0.998 7 1.41×10−9 0.999 7 90 1.77×10−9 0.999 6 1.78×10−9 0.999 3 110 2.64×10−9 0.996 8 2.45×10−9 0.999 4 130 2.65×10−9 0.997 5 4.16×10−9 0.997 1 25 kHz 4 h 70 1.23×10−9 0.999 2 1.27×10−9 0.999 9 90 2.04×10−9 0.998 8 2.07×10−9 0.999 6 110 2.08×10−9 0.984 4 2.83×10−9 0.967 9 130 3.99×10−9 0.998 1 2.50×10−9 0.976 5 40 kHz 2 h 70 8.30×10−10 0.996 6 1.05×10−9 0.998 5 90 1.71×10−9 0.997 1 1.56×10−9 0.998 6 110 2.68×10−9 0.999 6 2.03×10−9 0.980 2 130 3.10×10−9 0.999 9 2.79×10−9 0.961 3 40 kHz 4 h 70 1.23×10−9 0.998 9 1.24×10−9 0.999 9 90 2.80×10−9 0.996 9 2.28×10−9 0.993 8 110 2.91×10−9 0.987 4 3.21×10−9 0.991 4 130 3.06×10−9 0.986 6 3.51×10−9 0.997 9
下载: 导出CSV
表 5 污泥的表观活化能
Table 5. Values of apparent activation energy of sewage sludge
预处理
条件蒸发控制阶段 扩散控制阶段 Ea/
(kJ·mol−1)D0/
(m2·s−1)R2 Ea/
(kJ·mol−1)D0/
(m2·s−1)R2 无预处理 25.86 1.46×10−7 0.997 8 26.93 1.16×10−7 0.990 1 25 kHz 2 h 20.86 1.33×10−6 0.995 4 20.95 2.22×10−6 0.996 0 25 kHz 4 h 22.67 3.42×10−6 0.999 3 24.41 6.65×10−6 0.999 8 40 kHz 2 h 20.71 1.56×10−6 0.990 1 20.13 1.13×10−6 0.999 8 40 kHz 4 h 21.56 2.38×10−6 0.998 2 22.61 3.60×10−6 0.987 9
下载: 导出CSV
-
[1] LIN F, ZHU X, LI J, et al. Effect of extracellular polymeric substances (EPS) conditioned by combined lysozyme and cationic polyacrylamide on the dewatering performance of activated sludge[J]. Chemosphere, 2019, 235: 679-689. doi: 10.1016/j.chemosphere.2019.06.220 [2] CHEN L, LIAO Y, MA X. Economic analysis on sewage sludge drying and its co-combustion in municipal solid waste power plant[J]. Waste Management, 2021, 121: 11-22. doi: 10.1016/j.wasman.2020.11.038 [3] 张辰. 坚持系统思维科学处理推进污泥能源资源利用——《污泥无害化处理和资源化利用实施方案》解读[J]. 工程建设标准化, 2022(11): 36-37. [4] GUO J, CHEN M, HUANG Y, et al. Salinity effects on ultrasound-assisted hot air drying kinetics of sewage sludge[J]. Thermochimica Acta, 2019, 678: 178-298. [5] ZHANG Y, ABATZOGLOU N. Review: Fundamentals, applications and potentials of ultrasound-assisted drying[J]. Chemical Engineering Research and Design, 2020, 154: 21-46. doi: 10.1016/j.cherd.2019.11.025 [6] SUN G Y, CHEN M Q, HUANG Y W. Evaluation on the air-borne ultrasound-assisted hot air convection thin-layer drying performance of municipal sewage sludge[J]. Ultrasonics Sonochemistry, 2017, 34: 588-599. doi: 10.1016/j.ultsonch.2016.06.036 [7] 赵芳, 程道来, 陈振乾. 超声波处理对污泥热风干燥过程的影响[J]. 农业工程学报, 2015, 31(4): 272-276. doi: 10.3969/j.issn.1002-6819.2015.04.038 [8] 任黎晔, 朱易春, 张光明, 等. 低强度超声波对短程硝化污泥的影响[J]. 化工进展, 2020, 39(4): 1591-1596. [9] ZHAO F, CHEN Z. Numerical Study on Moisture Transfer in Ultrasound-Assisted Convective Drying Process of Sludge[J]. Drying Technology, 2011, 29(12): 1404-1415. doi: 10.1080/07373937.2011.568658 [10] ZHANG X Y, CHEN M Q, HUANG Y W, et al. Isothermal hot air drying behavior of municipal sewage sludge briquettes coupled with lignite additive[J]. Fuel, 2016, 171: 108-115. doi: 10.1016/j.fuel.2015.12.052 [11] CÁRCEL J A, NOGUEIRA R I, ROSSELLÓ C, et al. Influence on olive leaves (Olea europaea, var[J]. Serrana) antioxidant extraction kinetics of ultrasound assisted drying[C]//Defect and Diffusion Forum. Trans Tech Publications Ltd, 2010, 297: 1077-1082. [12] 张绪坤, 王高敏, 温祥东等. 基于图像处理的过热蒸汽与热风干燥污泥收缩特性分析[J]. 农业工程学报, 2016, 32(19): 241-248. doi: 10.11975/j.issn.1002-6819.2016.19.033 [13] WANG B B , LIU X T , CHEN J M, et al. Composition and functional group characterization of extracellular polymeric substances (EPS) in activated sludge: the impacts of polymerization degree of proteinaceous substrates[J]. Water Research, 2017, 129: 133-142. [14] 吴起. 基于傅里叶数法与优化法的污泥过热蒸汽干燥有效扩散系数研究[D]. 南昌: 南昌航空大学, 2015. [15] LI P, CHEN Z. Experiment study on porous fiber drying enhancement with application of power ultrasound[J]. Applied Acoustics, 2017, 127: 169-174. doi: 10.1016/j.apacoust.2017.06.003 [16] MIKKELSEN L H, KEIIDING K. Physico-chemical characteristics of full scale sewage sludges with implications to dewatering[J]. Water Research, 2002, 36(10): 2451-2462. doi: 10.1016/S0043-1354(01)00477-8 [17] 朱棵. 超声波换能器声阻抗梯度匹配层理论与方法的研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. [18] OZUNA C, ÁLVAREZ-ARENAS T G, RIERA E, et al. Influence of material structure on air-borne ultrasonic application in drying[J]. Ultrasonics sonochemistry, 2014, 21(3): 1235-1243. doi: 10.1016/j.ultsonch.2013.12.015 [19] ZHANG J, XUE Y, ESHTIAGHI N, et al. Evaluation of thermal hydrolysis efficiency of mechanically dewatered sewage sludge via rheological measurement[J]. Water Research, 2017, 116: 34-43. doi: 10.1016/j.watres.2017.03.020 [20] JING D, SHIFU G, XUJUN Y. Study on isothermal drying characteristics and kinetics model of lime sludge[J]. Chemical Equipment Technology, 2013, 34(6): 18-22. [21] XIAO H, ZhANH S, BAI J, et al. Air impingement drying characteristics of apricot[J]. Transactions of the Chinese Society of Agricultural Engineering, 2010, 26(7): 318-323. [22] MULET A, CÁRCEL J A, GARCÍA-PÉREZ J V, et al. Ultrasound-assisted hot air drying of foods[J]. Ultrasound technologies for food and bioprocessing, 2011: 511-534. [23] LI P, CHEN Z, SHENG L. Determination of optimum operation conditions in an ultrasound assisted fibrous porous media drying process[J]. Applied Thermal Engineering, 2018, 138: 394-402. doi: 10.1016/j.applthermaleng.2018.04.081 -
点击查看大图
图( 7) 表( 5)
计量
- 文章访问数: 1079
- HTML全文浏览数: 1079
- PDF下载数: 48
- 施引文献: 0
