橙酮是植物体内的次生代谢物,属于类黄酮类化合物中重要的一类,它较少在自然界中分布,主要存在于植物果实中[1]。由于它具有广泛的抗肿瘤、抗病毒、抗菌、抗炎、抗氧化和抗衰老等生物活性和药理作用[2-4],故被用作多种酶抑制剂[5]。研究发现,丝氨酸/苏氨酸激酶是生物酶中的一个大家族,它与白血病、肝癌等多种恶性肿瘤有关[6-7],DRAK2激酶即死亡相关凋亡诱导蛋白激酶2(death associated protein related apoptotic kinase 2),它是丝氨酸/苏氨酸激酶中的一种激酶[8],也是死亡相关蛋白激酶(DAPK)家族中的其中一种,该激酶在多种细胞的死亡信号通路中,发挥着非常关键的作用[9],它能诱导不同类型的细胞凋亡,所以对该类激酶抑制剂的研究受到人们的关注。但由于目前对DRAK2抑制剂的研究还存在明显的局限性[10],因此采用构效关系理论研究不失为一种安全有效的方法,特别是采用神经网络法对DRAK2抑制剂进行研究未见报道。
BP(back propagation)神经网络法是一种误差逆向传播算法,它是一种基于数据驱动的方法,估计精度高[11],该法是将计算机技术广泛应用于环境科学[12]、药学[13]、林学[14]、农学[15]、医学[16]、机械科学[17]、毒理学[18]、食品科学[19]、计算机科学[20]、纳米技术[21]等众多学科,是较为前沿的一种研究方法,该方法能模拟生命活动过程的神经网络行为,进行智能信息化的处理。为此在前期研究工作[22-24]基础上,根据文献[10]所列59个橙酮类DRAK2抑制剂分子的分子结构,认真剖析了橙酮类衍生物的分子结构与生物活性(pIC50)之间的关系,在分子的拓扑结构基础上,新定义了一种可以表征分子中原子特性的原子特征值(Ai),并对橙酮类衍生物苯环上连接的基团进行原子特征值的校正,从而建构一种新的分子结构指数——基团定位指数(D)。利用可对分子结构进行计算相关数据的应用软件,计算了59个橙酮类DRAK2抑制剂分子的电性距离矢量,并筛选了其中部分参数,将基团定位指数(D)与电性距离矢量两者有机结合,构建了可用于预测橙酮类DRAK2抑制剂分子生物活性的神经网络模型,所得活性预测结果较为令人满意,本研究工作成果对设计新的具有高抑制活性的橙酮类DRAK2抑制剂分子,有重要的实际指导意义。
1 基团定位指数的建构及生物活性数据来源(Construction of the group localization index and the source of biological activity data)
1.1 生物活性数据来源
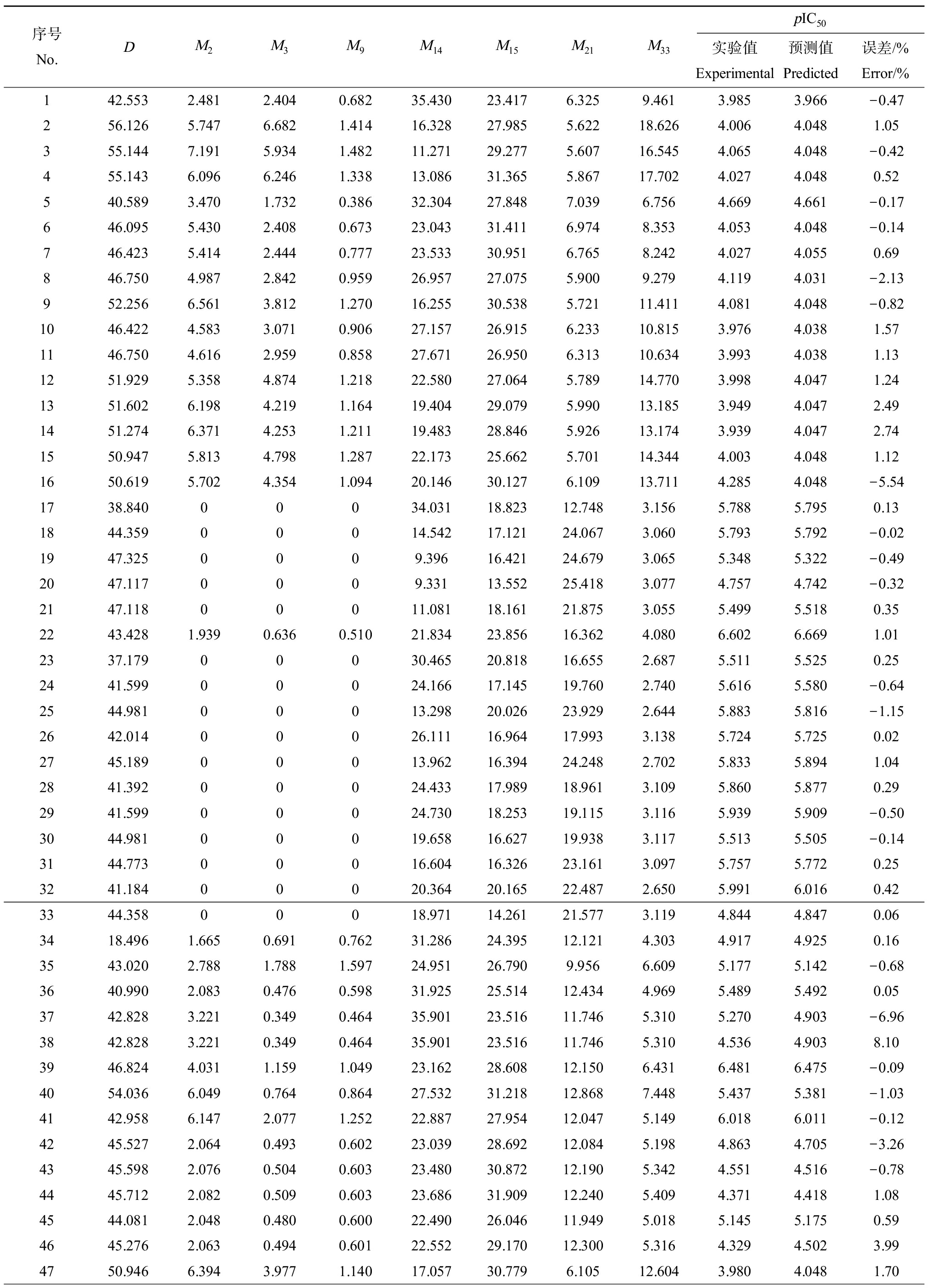
59个橙酮类DRAK2抑制剂分子及其生物活性值来源于文献[10],这些分子的母体结构见图1,具体连接的R1~R9基团的结构限于篇幅没有在本文列出(可参考文献[10]),将这些分子的抑制活性实验值pIC50(抑制活性值采用半数抑制浓度IC50的负对数pIC50表示)列于表1。
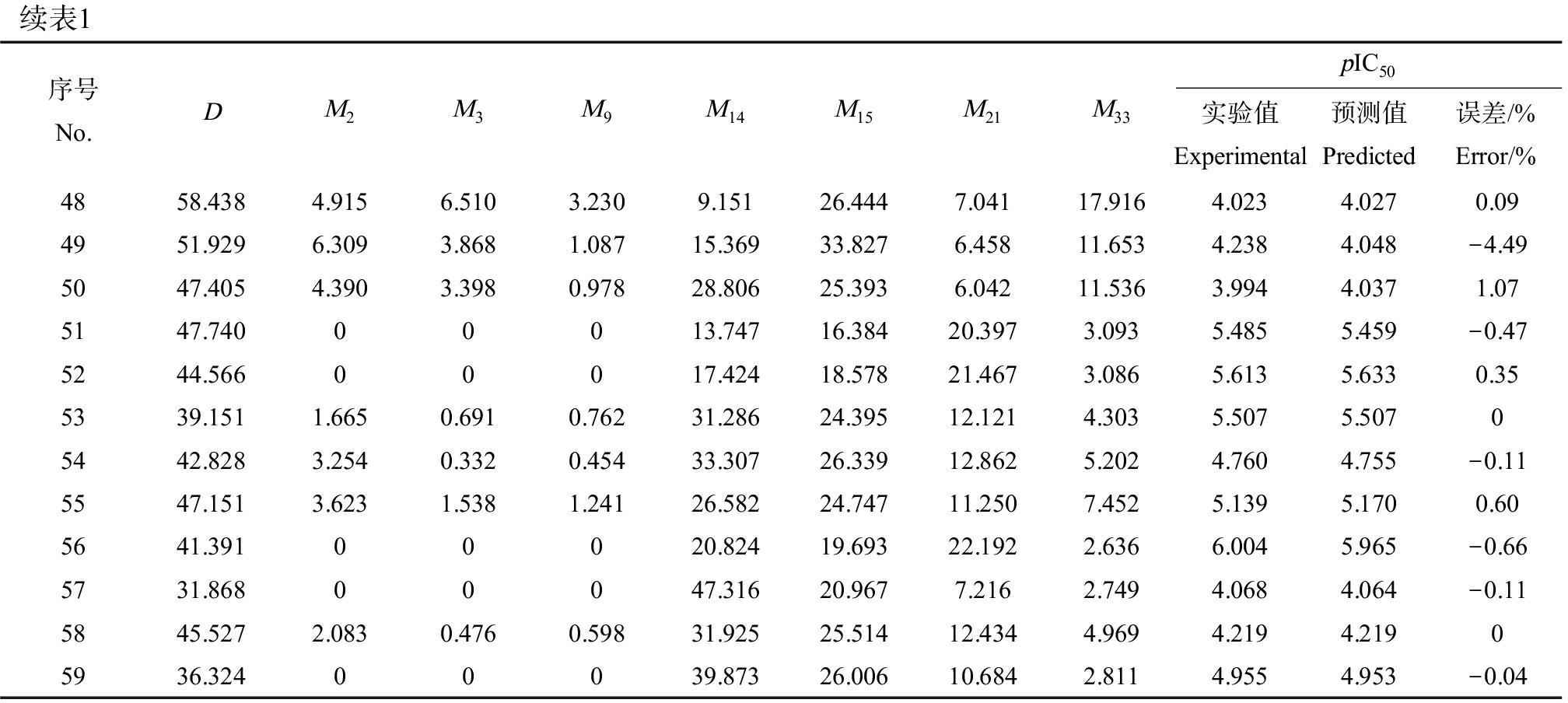
表1 橙酮衍生物的基团定位指数、电性距离矢量及其活性
Table 1 Group localization index, electrical distance vector and activity of aurone derivatives
序号No.DM2M3M9M14M15M21M33pIC50实验值Experimental预测值Predicted误差/%Error/%142.5532.4812.4040.68235.43023.4176.3259.4613.9853.966-0.47256.1265.7476.6821.41416.32827.9855.62218.6264.0064.0481.05355.1447.1915.9341.48211.27129.2775.60716.5454.0654.048-0.42455.1436.0966.2461.33813.08631.3655.86717.7024.0274.0480.52540.5893.4701.7320.38632.30427.8487.0396.7564.6694.661-0.17646.0955.4302.4080.67323.04331.4116.9748.3534.0534.048-0.14746.4235.4142.4440.77723.53330.9516.7658.2424.0274.0550.69846.7504.9872.8420.95926.95727.0755.9009.2794.1194.031-2.13952.2566.5613.8121.27016.25530.5385.72111.4114.0814.048-0.821046.4224.5833.0710.90627.15726.9156.23310.8153.9764.0381.571146.7504.6162.9590.85827.67126.9506.31310.6343.9934.0381.131251.9295.3584.8741.21822.58027.0645.78914.7703.9984.0471.241351.6026.1984.2191.16419.40429.0795.99013.1853.9494.0472.491451.2746.3714.2531.21119.48328.8465.92613.1743.9394.0472.741550.9475.8134.7981.28722.17325.6625.70114.3444.0034.0481.121650.6195.7024.3541.09420.14630.1276.10913.7114.2854.048-5.541738.84000034.03118.82312.7483.1565.7885.7950.131844.35900014.54217.12124.0673.0605.7935.792-0.021947.3250009.39616.42124.6793.0655.3485.322-0.492047.1170009.33113.55225.4183.0774.7574.742-0.322147.11800011.08118.16121.8753.0555.4995.5180.352243.4281.9390.6360.51021.83423.85616.3624.0806.6026.6691.012337.17900030.46520.81816.6552.6875.5115.5250.252441.59900024.16617.14519.7602.7405.6165.580-0.642544.98100013.29820.02623.9292.6445.8835.816-1.152642.01400026.11116.96417.9933.1385.7245.7250.022745.18900013.96216.39424.2482.7025.8335.8941.042841.39200024.43317.98918.9613.1095.8605.8770.292941.59900024.73018.25319.1153.1165.9395.909-0.503044.98100019.65816.62719.9383.1175.5135.505-0.143144.77300016.60416.32623.1613.0975.7575.7720.253241.18400020.36420.16522.4872.6505.9916.0160.423344.35800018.97114.26121.5773.1194.8444.8470.063418.4961.6650.6910.76231.28624.39512.1214.3034.9174.9250.163543.0202.7881.7881.59724.95126.7909.9566.6095.1775.142-0.683640.9902.0830.4760.59831.92525.51412.4344.9695.4895.4920.053742.8283.2210.3490.46435.90123.51611.7465.3105.2704.903-6.963842.8283.2210.3490.46435.90123.51611.7465.3104.5364.9038.103946.8244.0311.1591.04923.16228.60812.1506.4316.4816.475-0.094054.0366.0490.7640.86427.53231.21812.8687.4485.4375.381-1.034142.9586.1472.0771.25222.88727.95412.0475.1496.0186.011-0.124245.5272.0640.4930.60223.03928.69212.0845.1984.8634.705-3.264345.5982.0760.5040.60323.48030.87212.1905.3424.5514.516-0.784445.7122.0820.5090.60323.68631.90912.2405.4094.3714.4181.084544.0812.0480.4800.60022.49026.04611.9495.0185.1455.1750.594645.2762.0630.4940.60122.55229.17012.3005.3164.3294.5023.994750.9466.3943.9771.14017.05730.7796.10512.6043.9804.0481.70
续表1序号No.DM2M3M9M14M15M21M33pIC50实验值Experimental预测值Predicted误差/%Error/%4858.4384.9156.5103.2309.15126.4447.04117.9164.0234.0270.094951.9296.3093.8681.08715.36933.8276.45811.6534.2384.048-4.495047.4054.3903.3980.97828.80625.3936.04211.5363.9944.0371.075147.74000013.74716.38420.3973.0935.4855.459-0.475244.56600017.42418.57821.4673.0865.6135.6330.355339.1511.6650.6910.76231.28624.39512.1214.3035.5075.50705442.8283.2540.3320.45433.30726.33912.8625.2024.7604.755-0.115547.1513.6231.5381.24126.58224.74711.2507.4525.1395.1700.605641.39100020.82419.69322.1922.6366.0045.965-0.665731.86800047.31620.9677.2162.7494.0684.064-0.115845.5272.0830.4760.59831.92525.51412.4344.9694.2194.21905936.32400039.87326.00610.6842.8114.9554.953-0.04

图1 橙酮衍生物的母体结构
Fig. 1 Matrix structure of aurone derivatives
1.2 基团定位指数(D)的建构
构成分子的原子由于其价电子数、电子层数、电负性以及连接不同原子或基团等不尽相同,故会导致各个不同分子的物理化学特性也各不相同。橙酮衍生物的生物活性也与这些有关。通过考察文献[10]中59个橙酮类DRAK2抑制剂的抑制活性与分子结构之间的相互关系,新定义一种可用于表征分子中原子的物理化学特性的原子特征值(Ai)为:
Ai=(mi-hi)(χc+3)/(χi+3)
(1)
式中:mi、χi、hi分别为原子i的价电子数、鲍林电负性值、直接连接的氢原子个数,χc为碳原子的鲍林电负性。在邻接矩阵基础上,为此建构一种新的指数B。
B=∑(Ai)0.5
(2)
式中:B表示每一个原子对分子的贡献。通过考察橙酮类衍生物的结构,其母体2个苯环连接的基团及位置对活性的影响较大,为此对苯环上不同位置基团的特征值进行校正。
JR=B×(Ri+9)/10
(3)
式中:Ri为连接在苯环上的基团位置数。综合以上分析,确定一种新的分子结构指数。
D=∑(Ai)0.5+∑JR
(4)
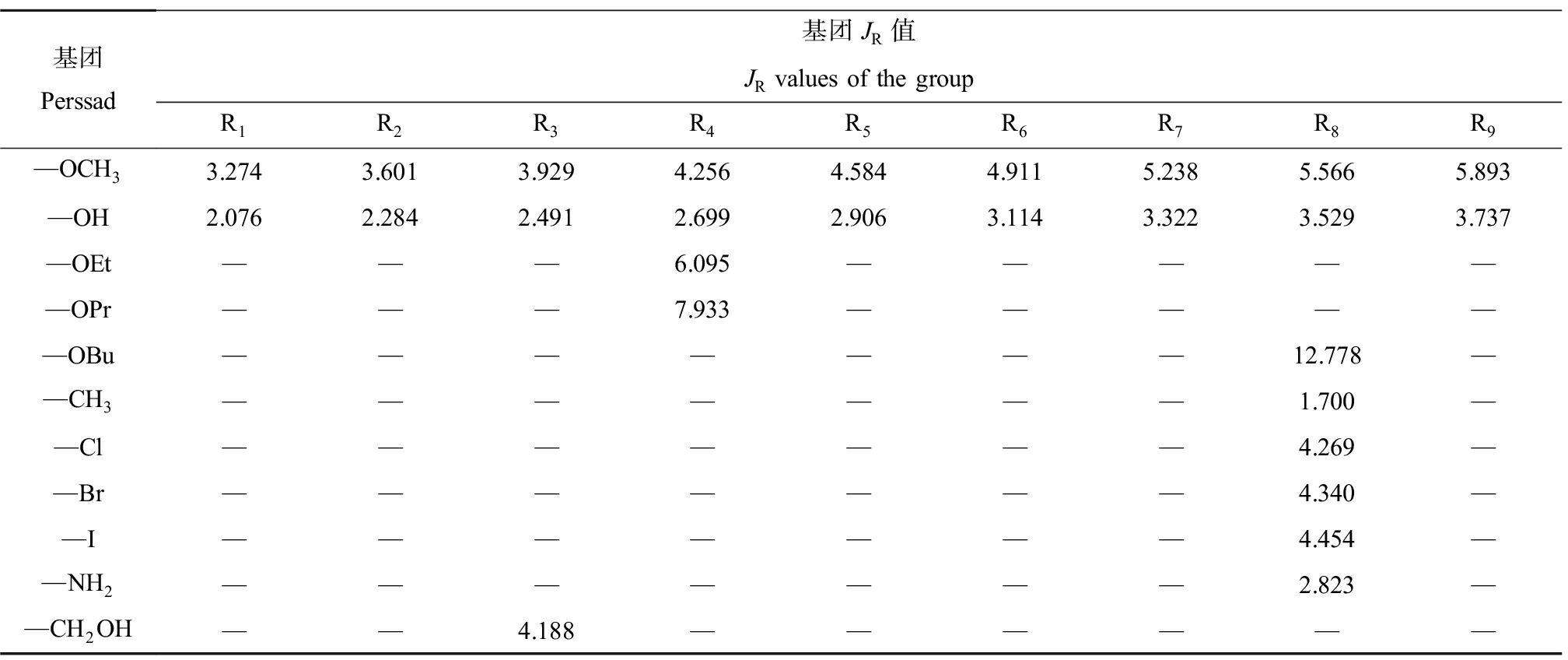
由于该指数充分考虑了衍生物苯环上连接基团本身的原子特征和所处位置对分子的贡献影响,故将其命名为基团定位指数,根据公式计算得到各位置基团的JR值列于表2中,59个橙酮类衍生物分子的D值列于表1中。
表2 苯环上不同位置基团的JR值
Table 2 The JR values of the groups at different positions on the benzene ring
基团Perssad基团JR值JR values of the groupR1R2R3R4R5R6R7R8R9—OCH33.2743.6013.9294.2564.5844.9115.2385.5665.893—OH2.0762.2842.4912.6992.9063.1143.3223.5293.737—OEt———6.095——————OPr———7.933——————OBu———————12.778——CH3———————1.700——Cl———————4.269——Br———————4.340——I———————4.454——NH2———————2.823——CH2OH——4.188——————
1.3 电性距离矢量的计算
由于化合物的生物活性所受影响因素较多,所以与单一分子结构指数之间的相关性一般不会很好,即单一指数不能完全反映化合物某种性质的变化规律,因此常常需要2种或2种以上指数有机结合,才能与化合物性质有好的相关性,为此,本法利用在众多研究中得到广泛应用的电性距离矢量[25-26]结构参数,将其与本文建构的基团定位指数协同,与橙酮类DRAK2抑制剂的生物活性进行回归分析。用Chemoffice绘图应用软件勾画出DRAK2抑制剂分子的分子结构,利用MATLAB计算软件自编程序[27],计算了59个DRAK2抑制剂分子的电性距离矢量值,通过回归分析发现,选择电性距离矢量的M2、M3、M9、M14、M15、M21、M33 7个结构参数与基团定位指数结合,与橙酮类DRAK2抑制剂的生物活性pIC50所得结果相对相关性最好,将计算得到的M2、M3、M9、M14、M15、M21、M33数据同样列于表1。
2 多元回归分析和神经网络模型建构(Multiple regression analysis and neural network model construction)
2.1 多元回归分析
将选择的电性距离矢量M2、M3、M9、M14、M15、M21、M33和基团定位指数(D)共8个参数为自变量,以橙酮类DRAK2抑制剂的生物活性pIC50为因变量,用SPSS回归分析应用软件进行多元回归,建立了预测DRAK2抑制剂生物活性的方程为:
pIC50=0.012D+0.072M2+0.556M3+0.396M9+0.051M14+0.039M15+0.175M21-0.267M33+0.498
(5)
式中:n为所取样本分子的样本数,r为结构指数与活性相关方程的相关系数,![]() 为方程的调整可决系数,S为方程的标准误差,F为Fischer精确检验的值。根据该式计算得到生物活性值与实验值的相对平均误差为5.83%,误差偏大,而且方程的相关系数为0.8535,说明分子结构参数与活性之间的相关性和预测结果并不十分理想。
为方程的调整可决系数,S为方程的标准误差,F为Fischer精确检验的值。根据该式计算得到生物活性值与实验值的相对平均误差为5.83%,误差偏大,而且方程的相关系数为0.8535,说明分子结构参数与活性之间的相关性和预测结果并不十分理想。
2.2 模型稳定性、离域值及预测能力检验
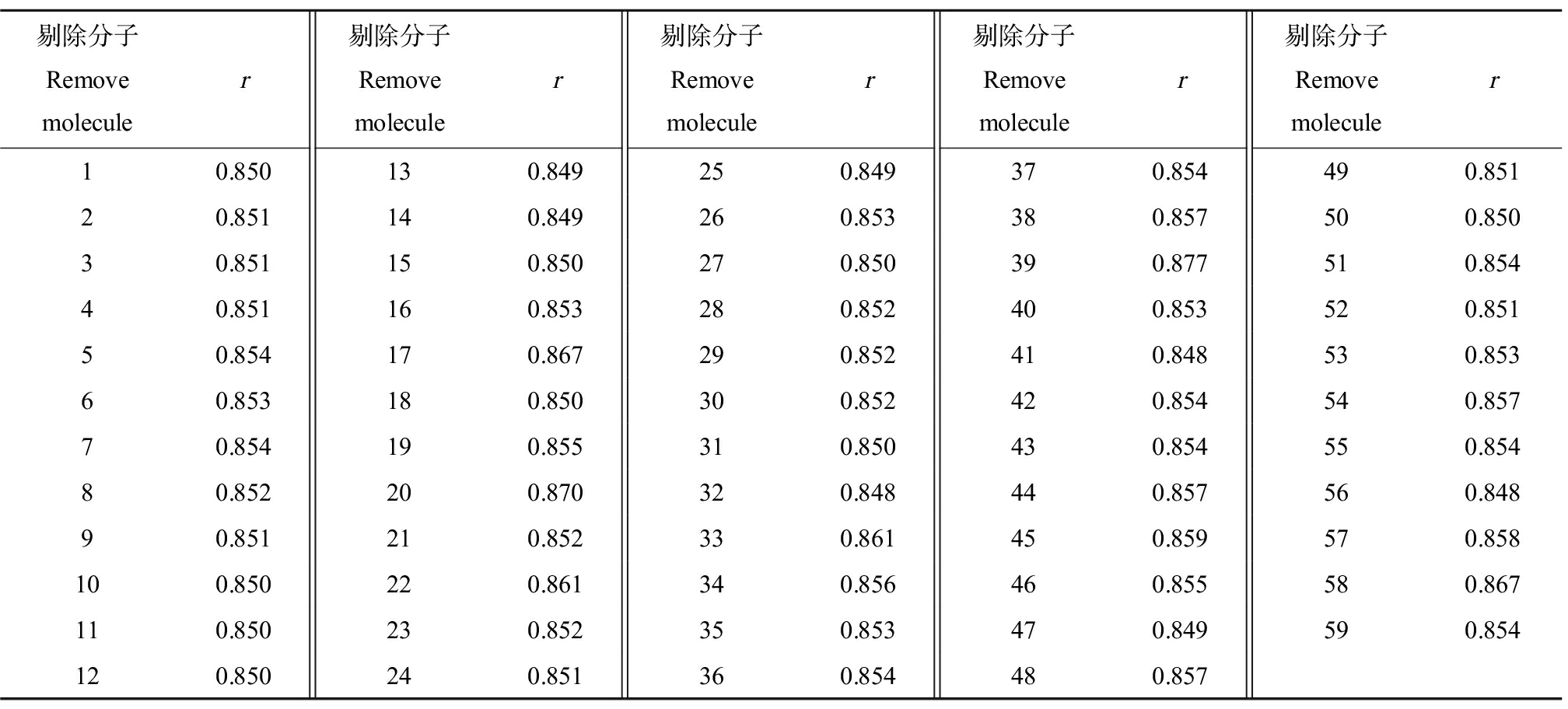
为检验预测DRAK2抑制剂生物活性的多元回归方程的稳定性及预测能力,这里先采用逐一剔除法对式(5)进行检验,即每次剔除1个DRAK2抑制剂分子,用余下的58个DRAK2抑制剂分子回归分析,这样共可以建立59个方程,得到59个相关系数(数据见表3),所有检验的相关系数平均值为0.8538,这里可以看出,检验的相关系数与式(5)的相关系数基本一致,说明预测活性模型(5)的稳定性较好;为了进一步建议模型的拟合优度、稳健性和预测能力,使用MINITAN软件对该活性预测模型进行留一法交互验证,计算得到模型交叉验证相关系数![]() 该值≥0.5,说明稳健性较好[28];再通过计算调整可决系数
该值≥0.5,说明稳健性较好[28];再通过计算调整可决系数![]() 交互验证相关系数
交互验证相关系数![]() 一般认为当两者的差值<0.3时,说明模型不存在“离域的异常数据”,没有过拟合现象,故模型既有较好的稳定性,预测能力也较强。因受篇幅限制,本文未将模型应用于其他样本进行试验,但由于指数D充分考虑分子中原子的电性和拓扑空间结构、基团的数量及连接等特性,可以预期应该也可以适用于类似分子的活性或毒性预测。
一般认为当两者的差值<0.3时,说明模型不存在“离域的异常数据”,没有过拟合现象,故模型既有较好的稳定性,预测能力也较强。因受篇幅限制,本文未将模型应用于其他样本进行试验,但由于指数D充分考虑分子中原子的电性和拓扑空间结构、基团的数量及连接等特性,可以预期应该也可以适用于类似分子的活性或毒性预测。
表3 检验的相关系数(r)
Table 3 Correlation coefficient (r) of inspection
剔除分子Remove moleculer剔除分子Remove moleculer剔除分子Remove moleculer剔除分子Remove moleculer剔除分子Remove moleculer10.850130.849250.849370.854490.85120.851140.849260.853380.857500.85030.851150.850270.850390.877510.85440.851160.853280.852400.853520.85150.854170.867290.852410.848530.85360.853180.850300.852420.854540.85770.854190.855310.850430.854550.85480.852200.870320.848440.857560.84890.851210.852330.861450.859570.858100.850220.861340.856460.855580.867110.850230.852350.853470.849590.854120.850240.851360.854480.857
表4 差异性比较
Table 4 Difference comparison

差异性比较Difference comparison文献[10]方法Literature [10] method本文方法The method of this paper建模方法Modeling method3D定量构效关系3D quantitative structure-activity relationship2D定量构效关系+神经网络法2D quantitative structure-activity relationship + neural network method创新性Innovativeness应用软件计算Application software calculation自定义新的结构指数+应用软件计算Customize the new structural index + application software calculation预测结果准确度Accuracy of the prediction results预测平均误差0.325(CoMFA)和0.231(CoMSIA),误差大The predicted mean errors of CoMFA and CoMSIA are 0.325 and 0.231 respectively, which are large预测平均误差0.052(相对误差1.12%),误差小The predicted mean error is 0.052(the relative error is 1.12%), which is small
2.3 变量D在模型中的作用
通过回归分析筛选电性距离矢量的M2、M3、M9、M14、M15、M21、M33结合基团定位指数(D),能与橙酮类DRAK2抑制剂生物活性值pIC50达到最优相关性,建立方程的相关系数为0.8535,如把方程中的变量D去除,只采用电性距离矢量的M2、M3、M9、M14、M15、M21、M33 7个变量与pIC50相关,方程的相关系数为0.8523,这里可以看出,即变量中增加基团定位指数(D)后,方程的相关性有所提高。最主要的是电性距离矢量的各个变量是对各基团的赋值,无法对不同的分子进行区分,而基团定位指数(D)则能区分每一个不同分子,具有较强的结构差异区分能力。
2.4 模型的差异性比较
本文采用神经网络方法研究建立预测模型与文献采用的3D定量构效关系研究方法,两者有一定的区别,具体差异性主要表现在以下几个方面。
2.5 神经网络预测模型
由于采用多元回归方程预测结果并不理想,为提高预测准确度,解决结构参数与生物活性的非线性关系问题,采用神经网络方法进一步研究。神经网络是一种智能算法,它主要由输入节点层、隐含节点层、输出节点层3层结构组成。将式(5)中的电性距离矢量M2、M3、M9、M14、M15、M21、M33和基团定位指数(D)结合,将它们作为神经网络3层结构中的输入节点层的参数(该值即为8),59种橙酮类DRAK2抑制剂的抑制活性pIC50作为3层结构中输出节点层参数(该值即为1),隐含节点层参数值,则取Andrea和Kalayeh[29]、许禄和邵学广[30]规则综合后得到:
2.2>n/[(Si+2)H+1]≥1.4
(6)
式中:n为样本分子的总数,Si、H则为神经网络3层结构中的输入节点层参数值、隐含节点层参数值。根据此式计算可得H取值为3或4,经计算分析比较,发现H采用4时,建立方程所得结果较为理想,为此网络结构采用8-4-1的结构方式。为防止过度拟合,将59个橙酮类DRAK2抑制剂分子分为训练集、测试集和验证集,训练集为每5个分子组成一组的第1、3、5个分子,测试集为每组的第2个分子,验证集为每组的第4个分子。由此建构的预测橙酮类DRAK2抑制剂活性的神经网络模型的总相关系数(r总)达到0.9931,3个集合的相关系数:训练集r训练达到0.9929,测试集r测试达到0.9914,验证集r验证达到0.9964,从数据可以看出,无论训练集、测试集、验证集三者之间还是与总相关系数较为接近,吻合度较好,而且相关系数均超过了0.99,属于优级相关,说明橙酮类DRAK2抑制剂分子的电性距离矢量和基团定位指数与抑制剂的抑制活性之间是非线性关系,而不是线性关系,利用新建构的神经网络模型预测橙酮类DRAK2抑制剂的生物抑制活性,抑制活性的预测值与其实验值之间的相对平均误差只有1.12%,神经网络法预测相对误差只有多元回归方法预测误差的1/5,明显比多元回归法计算得到的相对平均误差5.83%要小,说明神经网络法模型对抑制剂抑制活性的预测精度更好。对神经网络法预测值与实验值、多元回归法预测值与实验值分别作关系图(图2和图3),明显可以看出,神经网络法的活性预测值与实验值的对应值都紧靠45°直线,而多元回归法活性预测值则较为分散,说明神经网络法对橙酮类DRAK2抑制剂的活性预测结果比较可靠。将神经网络法对生物抑制活性pIC50预测值也列入表1。
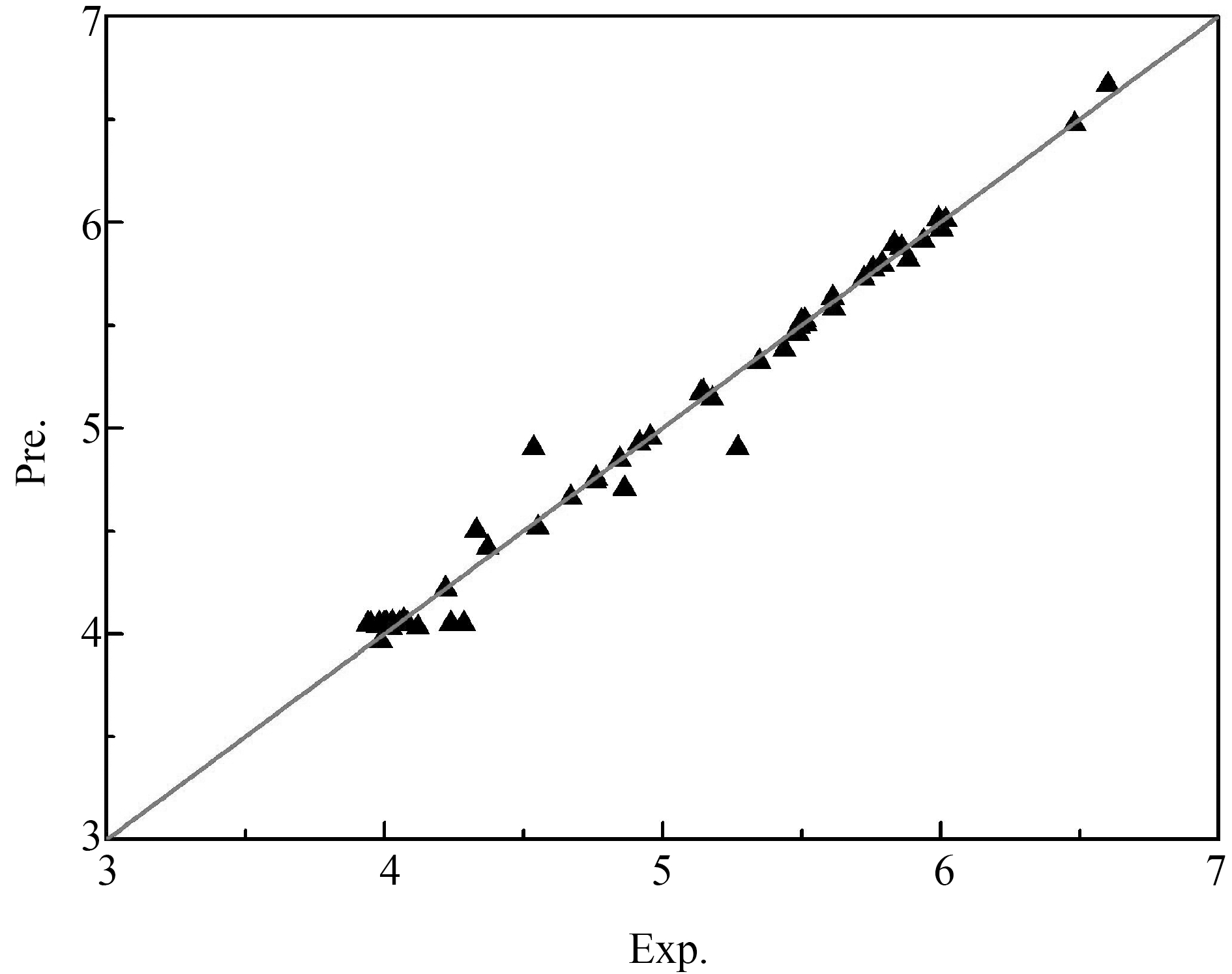
图2 pIC50神经网络法预测值与实验值的关系
Fig. 2 Relationship between predicted and experimental values of pIC50 by neural network method

图3 pIC50多元回归法预测值与实验值的关系
Fig. 3 Relationship between predicted and experimental values of pIC50 by multiple regression method
3 结果讨论(Results and discussion)
通过分析橙酮类DRAK2抑制剂的分子结构与其生物活性之间的关系可以看出,当橙酮类抑制剂母体苯环上连接的为给电子基团时,其活性会增大,且基团的极性越大,其生物活性越强;如连接的为吸电子基团时,则活性会降低;如1号和17号分子、3号和20号分子、9号和27号分子、10号和28号分子等等,在2个苯环上连接有—OH的分子活性明显高于对应位置连接有—OCH3的分子活性;又如R8位连接的吸电子基团—Cl、—Br、—I分子的活性明显小于同一位置连接给电子基团—NH2的分子活性。所以基团的极性大小、苯环上连接的基团的数量等等,均会影响分子活性的大小,本文定义的原子特征值并通过对基团连接位置校正而建构的新的基团定位指数,能蕴含分子活性的这一变化规律,并将其与电性距离矢量进行结合,从而建立预测橙酮类DRAK2抑制剂生物活性的神经网络模型,根据神经网络模型预测的结果可以看出,总体可靠性较好,各个分子的相对误差较小,只有对38号分子的预测误差达8.10%,稍显偏大,这可能与R4位连接的—OPr链稍长,而其活性实验值明显偏小有关,但总体而言,本文建构的神经网络理论模型对设计活性大的橙酮类DRAK2抑制剂分子,可起到重要的实际理论指导作用。
综上所述,本研究表明:
(1) 定义了新的原子特征值,并建构了一种新的分子结构指数——基团定位指数(D),并与优化筛选电性距离矢量中获得的M2、M3、M9、M14、M15、M21、M33 7个结构参数有机结合,8种指数与橙酮类DRAK2抑制剂生物抑制活性之间有良好的非线性关系,按照神经网络8-4-1的网络结构,建立的橙酮类DRAK2抑制剂活性的神经网络法预测模型的总相关系数达到了0.9931的优级相关,生物抑制活性的预测值与实验值之间的相对平均误差只有1.12%,该预测结果明显优于多元回归法活性预测值与实验值的相对平均误差5.83%,说明橙酮类DRAK2抑制剂的分子结构参数与其生物活性值(pIC50)之间具有好的非线性关系,而不是简单的线性关系。
(2) 橙酮类DRAK2抑制剂生物活性的大小,除与橙酮类DRAK2抑制剂分子的2个苯环上相连接基团的极性大小有关外,还与这些基团连接的数量多少、连接在苯环上所处的位置等等空间特性有很大的关系,当所连接的基团极性越大活性越强,基团所处位置受周围相邻的原子或基团影响较大时也会影响活性的大小。
[1] 刘斌, 张敏, 谢龙观, 等. 橙酮衍生物的合成、晶体结构及除草活性[J]. 高等学校化学学报, 2011, 32(10): 2335-2340
Liu B, Zhang M, Xie L G, et al. Synthesis, crystal structure and herbicidal activity of aurone derivatives [J]. Chemical Journal of Chinese Universities, 2011, 32(10): 2335-2340 (in Chinese)
[2] 黄新炜, 王征, 陈巧利, 等. 橙酮衍生物的合成及初步抗肿瘤活性研究[J]. 有机化学, 2013, 33(12): 2565-2571
Huang X W, Wang Z, Chen Q L, et al. Synthesis and preliminary antitumor activities of aurone derivatives [J]. Chinese Journal of Organic Chemistry, 2013, 33(12): 2565-2571 (in Chinese)
[3] Socha R, Ga kowska D, Bugaj M, et al. Phenolic composition and antioxidant activity of propolis from various regions of Poland [J]. Natural Product Research, 2015, 29(5): 416-422
kowska D, Bugaj M, et al. Phenolic composition and antioxidant activity of propolis from various regions of Poland [J]. Natural Product Research, 2015, 29(5): 416-422
[4] Cho J K, Curtis-Long M J, Lee K H, et al. Geranylated flavonoids displaying SARS-CoV papain-like protease inhibition from the fruits of Paulownia tomentosa [J]. Bioorganic &Medicinal Chemistry, 2013, 21(11): 3051-3057
[5] 马淑玥. 香豆素/橙酮衍生物制备及阴离子识别和脂滴成像研究[D]. 济南: 济南大学, 2021: 1
Ma S Y. Preparation, anion recognition and lipid droplet imaging of coumarin/aurone derivatives [D]. Jinan: University of Jinan, 2021: 1 (in Chinese)
[6] 郑建涛, 张承英. 丝氨酸/苏氨酸激酶15蛋白在结肠癌的表达[J]. 福建医科大学学报, 2007, 41(2): 134-136
Zheng J T, Zhang C Y. Expression of serine/theronine kinase 15 in colorectal carcinoma [J]. Journal of Fujian Medical University, 2007, 41(2): 134-136 (in Chinese)
[7] 祝昊丹, 倪艳秀, 茅爱华, 等. 丝氨酸/苏氨酸激酶对猪链球菌2型应激和毒力的影响[J]. 江苏农业学报, 2016, 32(3): 593-600
Zhu H D, Ni Y X, Mao A H, et al. The impact of serine/threonine kinase on stress response and virulence of Streptococcus suis type 2 [J]. Jiangsu Journal of Agricultural Sciences, 2016, 32(3): 593-600 (in Chinese)
[8] 李仲诚, 阮礼波, 杨帆, 等. 死亡相关凋亡诱导蛋白激酶2(DRAK2)研究进展[J]. 生命科学, 2014, 26(8): 823-828
Li Z C, Ruan L B, Yang F, et al. Study of the DRAK2 [J]. Chinese Bulletin of Life Sciences, 2014, 26(8): 823-828 (in Chinese)
[9] 张正, 戴成球, 吴红红, 等. 烷基酚类死亡相关凋亡诱导蛋白激酶2(DRAK2)小分子抑制剂的设计与合成研究[J]. 有机化学, 2021, 41(8): 3204-3213
Zhang Z, Dai C Q, Wu H H, et al. Design and synthesis of alkyl phenols inhibitors of death associated apoptotic protein kinase 2 (DRAK2) [J]. Chinese Journal of Organic Chemistry, 2021, 41(8): 3204-3213 (in Chinese)
[10] 李逸, 王边琳, 牛超, 等. 橙酮类DRAK2抑制剂的3D-QSAR及分子对接研究[J]. 化学通报, 2022, 85(6): 728-735
Li Y, Wang B L, Niu C, et al. Study on 3D quantitative structure-activity relationship and molecular docking of aurone DRAK2 inhibitors [J]. Chemistry Bulletin, 2022, 85(6): 728-735 (in Chinese)
[11] Xia B Z, Cui D Y, Sun Z, et al. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network [J]. Energy, 2018, 153: 694-705
[12] 黄刚. 基于BP神经网络的大气环境监测点布置多目标优化研究[J]. 环境科学与管理, 2021, 46(5): 130-134
Huang G. Multi-objective optimization of atmospheric environment monitoring point layout based on BP neural network [J]. Environmental Science and Management, 2021, 46(5): 130-134 (in Chinese)
[13] 杨岩, 肖佳妹, 王韧, 等. 人工神经网络在中药相关研究领域的应用[J]. 中草药, 2019, 50(13): 3230-3236
Yang Y, Xiao J M, Wang R, et al. Application of artificial neural network in research of Chinese materia medica [J]. Chinese Traditional and Herbal Drugs, 2019, 50(13): 3230-3236 (in Chinese)
[14] 程冀文, 王树森, 罗于洋, 等. 基于BP神经网络的沙柳地上生物量预测模型[J]. 林业科学研究, 2022, 35(3): 193-198
Cheng J W, Wang S S, Luo Y Y, et al. Aboveground biomass model of Salix psammophila based on BP neural network [J]. Forest Research, 2022, 35(3): 193-198 (in Chinese)
[15] 金武, 何奇, 杜兴伟, 等. 基于江苏省河蟹主产区气象因子的产量BP神经网络预测[J]. 农学学报, 2022, 12(6): 50-54
Jin W, He Q, Du X W, et al. Prediction of crab yield by BP neural network based on meteorological factors of crab producing areas in Jiangsu [J]. Journal of Agriculture, 2022, 12(6): 50-54 (in Chinese)
[16] Maher G, Wilson N, Marsden A. Accelerating cardiovascular model building with convolutional neural networks [J]. Medical &Biological Engineering &Computing, 2019, 57(10): 2319-2335
[17] Di Mauro A, Chen H, Sick V. Neural network prediction of cycle-to-cycle power variability in a spark-ignited internal combustion engine [J]. Proceedings of the Combustion Institute, 2019, 37(4): 4937-4944
[18] 堵锡华, 陈艳, 宋明, 等. 神经网络用于卤代肉桂酸对羊角月牙藻毒性的预测研究[J]. 生态毒理学报, 2021, 16(3): 347-354
Du X H, Chen Y, Song M, et al. Predictive study on toxicity of halogenated cinnamic acid to Selenastrum capricornutum by neural network method [J]. Asian Journal of Ecotoxicology, 2021, 16(3): 347-354 (in Chinese)
[19] 堵锡华, 李靖, 田林, 等. 杜松籽油香气成分的理论分析模型[J]. 云南大学学报(自然科学版), 2019, 41(1): 136-143
Du X H, Li J, Tian L, et al. Theoretical analysis model of aroma components of juniper berry oil [J]. Journal of Yunnan University (Natural Sciences Edition), 2019, 41(1): 136-143 (in Chinese)
[20] Lathuilière S, Massé B, Mesejo P, et al. Neural network based reinforcement learning for audio-visual gaze control in human-robot interaction [J]. Pattern Recognition Letters, 2019, 118: 61-71
[21] Curtis C, McKenna M, Pontes H, et al. Predicting in situ nanoparticle behavior using multiple particle tracking and artificial neural networks [J]. Nanoscale, 2019, 11(46): 22515-22530
[22] 堵锡华, 田林, 徐艳, 等. 枣花及枣花蜜香气成分保留指数的神经网络法研究[J]. 西南大学学报(自然科学版), 2021, 43(9): 142-152
Du X H, Tian L, Xu Y, et al. Study on the retention index of aroma components of jujube flower and jujube honey with the neural network method [J]. Journal of Southwest University (Natural Science Edition), 2021, 43(9): 142-152 (in Chinese)
[23] 堵锡华, 王超. 醇和酚类污染物对欧洲林蛙蝌蚪及梨形四膜虫毒性的定量结构-活性模型[J]. 生态毒理学报, 2018, 13(6): 250-258
Du X H, Wang C. Quantitative structure-activity model of toxicity of alcohol and phenolic pollutants to Rana temporaria tadpoles and Tetrahymena pyriformis [J]. Asian Journal of Ecotoxicology, 2018, 13(6): 250-258 (in Chinese)
[24] 堵锡华, 吴琼, 李靖, 等. 有机污染物色度降解动力学常数的神经网络研究[J]. 徐州工程学院学报(自然科学版), 2022, 37(4): 30-35
Du X H, Wu Q, Li J, et al. Neural network study on kinetic constants of chromatic degradation of organic pollutants [J]. Journal of Xuzhou Institute of Technology (Natural Sciences Edition), 2022, 37(4): 30-35 (in Chinese)
[25] 陈艳, 冯惠, 周俊, 等. HIV-1整合酶链转移抑制剂的QSAR研究与分子设计[J]. 南京理工大学学报, 2021, 45(6): 716-721
Chen Y, Feng H, Zhou J, et al. QSAR study on HIV-1 integrase chain transfer inhibitors and their molecular design [J]. Journal of Nanjing University of Science and Technology, 2021, 45(6): 716-721 (in Chinese)
[26] 朱利兰, 杜少辉, 冯长君. 基于ANN研究芳烷基哌嗪衍生物的镇痛活性[J]. 化学研究与应用, 2021, 33(6): 1098-1103
Zhu L L, Du S H, Feng C J. Research on the analgesic activity of aralkyl piperazinyl derivatives based on artificial neural network [J]. Chemical Research and Application, 2021, 33(6): 1098-1103 (in Chinese)
[27] 张婷, 梁逸曾, 赵晨曦, 等. 基于分子结构预测气相色谱程序升温保留指数[J]. 分析化学, 2006, 34(11): 1607-1610
Zhang T, Liang Y Z, Zhao C X, et al. Prediction of temperature-programmed retention indices from molecule structures [J]. Chinese Journal of Analytical Chemistry, 2006, 34(11): 1607-1610 (in Chinese)
[28] 刘海春, 卢帅, 冉挺, 等. 基于分子对接和QSAR方法预测B-Raf Ⅱ型抑制剂活性[J]. 物理化学学报, 2015, 31(11): 2191-2206
Liu H C, Lu S, Ran T, et al. Accurate activity predictions of B-Raf type Ⅱ inhibitors via molecular docking and QSAR methods [J]. Acta Physico-Chimica Sinica, 2015, 31(11): 2191-2206 (in Chinese)
[29] Andrea T A, Kalayeh H. Applications of neural networks in quantitative structure-activity relationships of dihydrofolate reductase inhibitors [J]. Journal of Medicinal Chemistry, 1991, 34(9): 2824-2836
[30] 许禄, 邵学广. 化学计量学方法[M]. 2版. 北京: 科学出版社, 2004: 441