-
曝气生物滤池(biological aerated filter, BAF)是将生物氧化和截留吸附结合的新型好氧污水处理工艺,具有流程简单、处理效率高等优点[1]。按照其进水方式可分为上向流和下向流[2],其中,上向流滤池不仅布水和布气均匀、不易堵塞,而且防止了滤料的流失[3],因而应用较广泛[4-6]。此外,BAF池型一般为长方体,这便于施工和曝气管道布置,故很多设计研究中都选用该池型[7-8]。当污水流经滤料表面时,水中的溶解氧也向生物膜内扩散,污水中的有机物在滤料表面微生物的生化作用下得到有效降解,最终转化成CO2和H2O等代谢产物[9-11]。因此,良好的曝气可有效地提高对污染物的去除效果。本研究旨在通过数值模拟探究出较好的曝气方式及曝气效果。
近年来,BAF曝气方面的相关研究多以实验和数值模拟为主。在BAF反冲洗的研究方面,张杰等[1]通过BAF反冲洗特性实验研究出脉冲气冲和连续水冲的组合比气水同时反洗要好;李微等[12]采用间歇曝气/曝气生物滤池工艺探究脱氮除磷的效果,通过定量控制一级及二级曝气量达到了较好的脱氮除磷效果;杨春娣[13]采用模型实验和数值模拟结合的方法,通过控制水深纵横比及曝气孔径,使气液两相流场分布均匀、混合充分;刘玉玲等[14]对推流式曝气池进行了数值模拟研究,通过对流场结构的分析探索出提高氧气利用率、减少能耗的方法。
目前,有关BAF曝气管道布置方式的直接研究较少,采用数值模拟研究方法也很少。本研究以某污水处理厂采用前置反硝化曝气生物滤池的曝气管道系统为对象,首先进行二维数值模拟,探索中心枝状、单边枝状和环状曝气方式的优劣,然后通过三维数值模拟对拟采用的基于二维数值模拟所确定的较好曝气方式的曝气均匀性及效率进行定量确认。本研究运用数值模拟方法,将定性和定量地表达曝气系统的流场分布情况,可快速、准确地找出较好的曝气方式,从而为曝气生物滤池的选型设计提供参考。
全文HTML
-
守恒方程包括质量守恒方程和动量守恒方程[15],如式(1)和式(2)所示。
式中:ρ为流体密度,kg·m−3;t为流动时间,s;x、y、z分别为直角坐标系的3个互相垂直方向的距离,m;u、v、w分别为x、y、z方向的速度,m·s−1。
式中:ρ为流体密度,kg·m−3;µ和µt分别为流体分子动力黏度和涡动力黏度,kg·(m·s)−1;g为重力加速度,m·s−2;p为雷诺平均压力,Pa。
-
本研究采用适用范围广、计算经济且被广泛应用于工业流场模拟的湍流标准k-ε模型,通过求解湍流动能k[16]和耗散率ε[16]方程,从而对涡黏度µt[16]进行求解。湍流动能k对应的输运方程见式(3)。耗散率ε的输运方程见式(4)。湍动黏度µt的方程见式(5)。
式中:Gk为平均速度梯度引起的湍动能k的产生项;YM为可压湍流中脉动扩张的贡献;σk和σε分别为与湍动能k和耗散率ε对应的普朗特数,取值为1.0和1.3;Sk和Sε分别为定义的湍动能源项和湍流耗散源项;Cµ为经验常数,取值为0.09;C1ε为经验常数,取值为1.44;C2ε为经验常数,取值为1.92。
-
在对连续性方程、动量方程求解时,都必须先确定求解初始条件和边界条件,而边界条件的设定对求解结果的影响十分关键[17-18]。本研究根据入口流量定义了曝气干管的速度入口,出口则根据曝气孔的设置深度定义为压力出口,管壁设定为给定粗糙度的固体界面。本研究采用专业模拟软件Fluent对曝气管道进行数值模拟求解。采用的数值求解方法为有限体积法,其具有很好的守恒性,可以克服泰勒公式展开出现离散的缺点且对网格的适应性很好。其中:对时变项,采用二阶精度的隐式格式的三时间段法;对对流项,采用二阶精度的迎风格式;对扩散项,采用二阶精度的中心差分格式。
研究对应的数值模拟过程中用到的基本参数如表1所示。
1.1. 守恒方程
1.2. 湍流模型
1.3. 边界条件
-
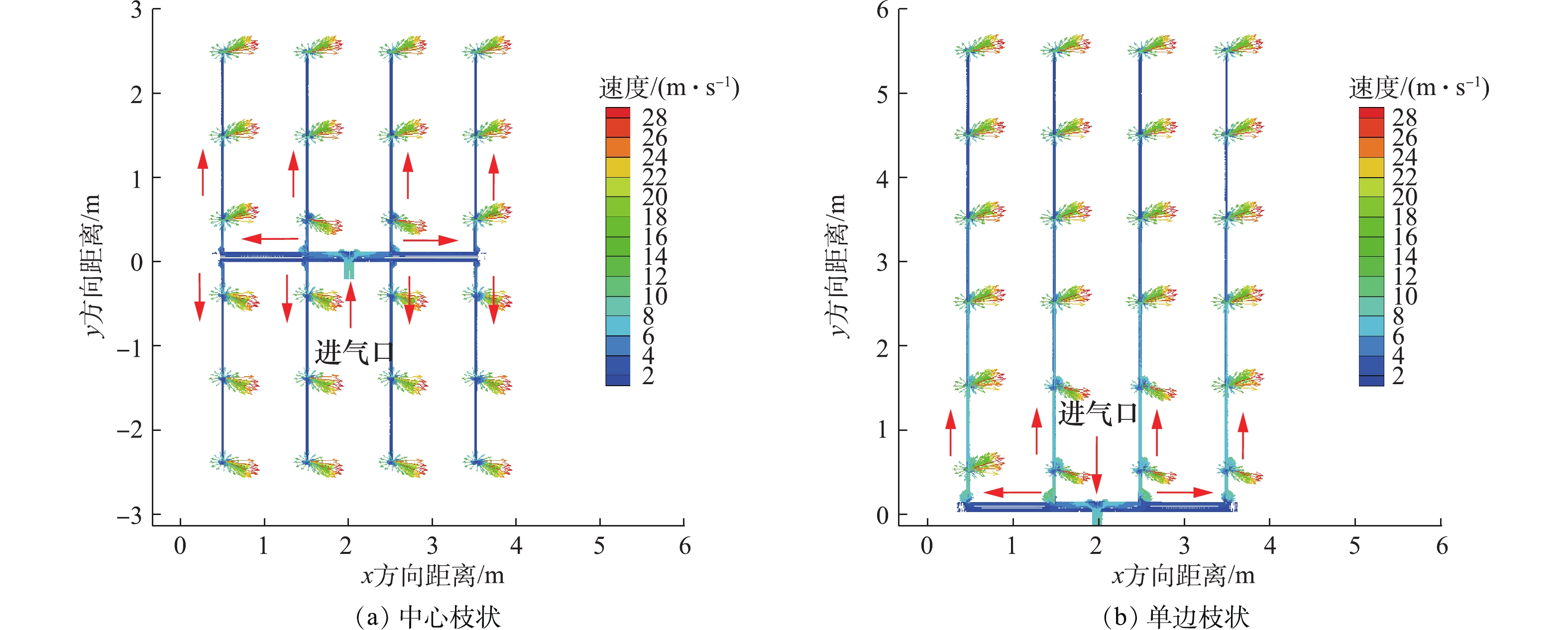
二维数值模拟研究了中心枝状、单边枝状和环状的3种曝气方式。中心枝状是指气体从中间干管位置进入,干管两侧支管对称分布(见图1(a));单边枝状是指气体从干管进入,支管布置在干管一侧(见图1(b));环状是指气体从干管进入,干管为环状,支管均匀分布在干管上(见图2(a))。这3种不同的曝气管道系统的干管、支管管径相同,分别为100 mm及20 mm;干管的入流速度根据所需曝气量取为8 m·s−1,出口根据水厂的水下管道设置深度定为50 000 Pa的压力出口;曝气管道上孔口按照等间距设置成圆形,孔口直径为2 mm。
模拟所得中心及单边枝状曝气方式的二维速度场分别如图1(a)和图1(b)所示。可见气体自干管的中间位置进入管道后,经支管到达曝气孔,几乎均匀地从各个曝气孔流出。
环状曝气方式的管道及局部流场模拟结果如图2所示。图2(a)为以水厂原型的管道系统气体流动的二维速度分布。气体由右侧中间的干管入口进入,图2(a)下面b、c处分别为环状干管的弯角处,图2(b)上部d为位于环状系统中间对称面的代表部分。图2(b)弯管处的曝气量和干管直管处的图2(d)相比较少;图2(c)的干管弯管处附近的曝气孔几乎无曝气。进一步观察干管弯管处的气体流动可见,其靠近连接支管处的气体流动较快,由伯努利方程[19]可知,该处的压力小,产生了相对的负压,致使环状管网角部出气量少或者没有检测到出气量。模拟结果表明,应该避免环状曝气管网的设计,以提高滤池角部的曝气均匀性。
-
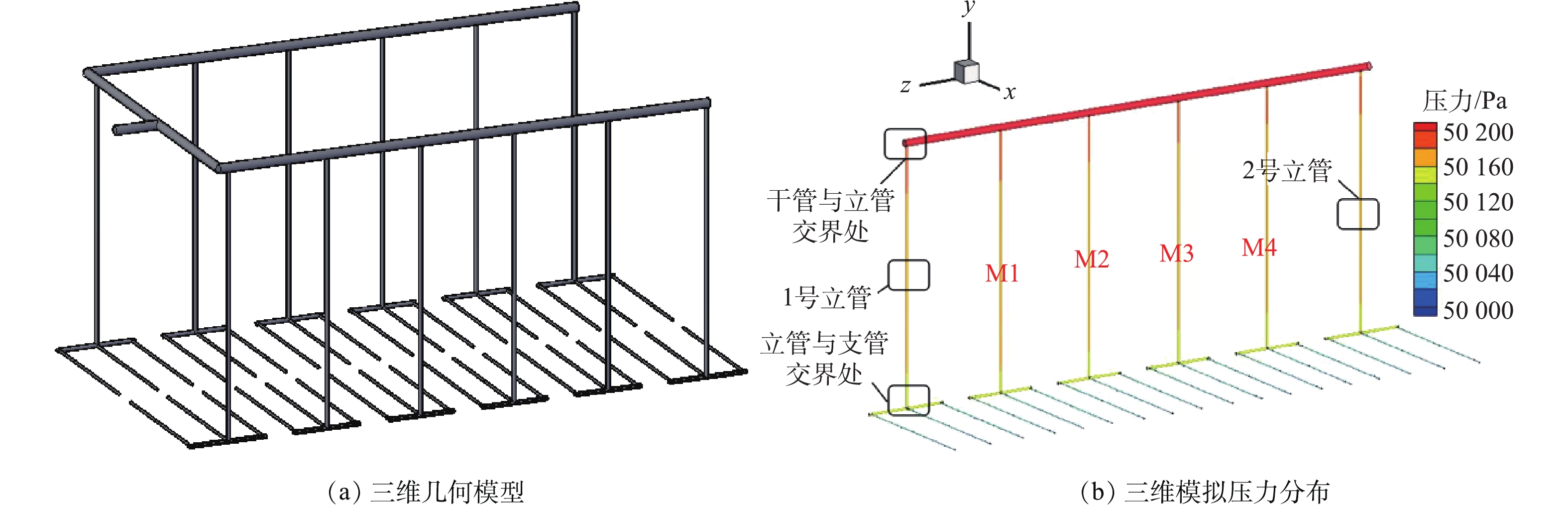
根据二维模拟的结果,水厂拟采用如图3(a)所示的类似中心枝状的曝气管道系统。与图1(a)模型中的中心支状相比:二者相同点在于均以进气干管为对称轴,以保证干管左右两侧进气量均分;不同点在于中心支状的结构分布更均匀些,但实际安装、运行费用等方面存在不足。三维数值模拟对其曝气效果进行了模拟确认。根据其对称性,为提高模拟效益,取如图3(b)所示的一侧模拟即可。模拟的主要关注点是曝气量是否达到各个角落,其次是各个支管的曝气是否均匀。研究设计基本参数如下:水平干管、支管(立管)及下部水平曝气管的管径分别为150、50和20 mm;立管长为5.3 m,曝气管长为3 m。总曝气量为6 m3·min−1,根据对称性,模拟时半边取3 m3·min−1;曝气孔在水下5 m,取50 000 Pa为模拟的气体出口压力。由图3(b)所示的整体压力分布可以看出,管道压力自左侧气体入口至曝气管压力逐级减小,这说明曝气过程是基本均匀且为压力驱动的。
研究分别选择离进气口最近的1号立管及最远的2号立管进行对比分析,若二者差别不大,那么基本可判定整体供气是均匀的。依次观察分析干管与立管交界处、立管与支管交界处以及曝气管的流场分布情况。
-
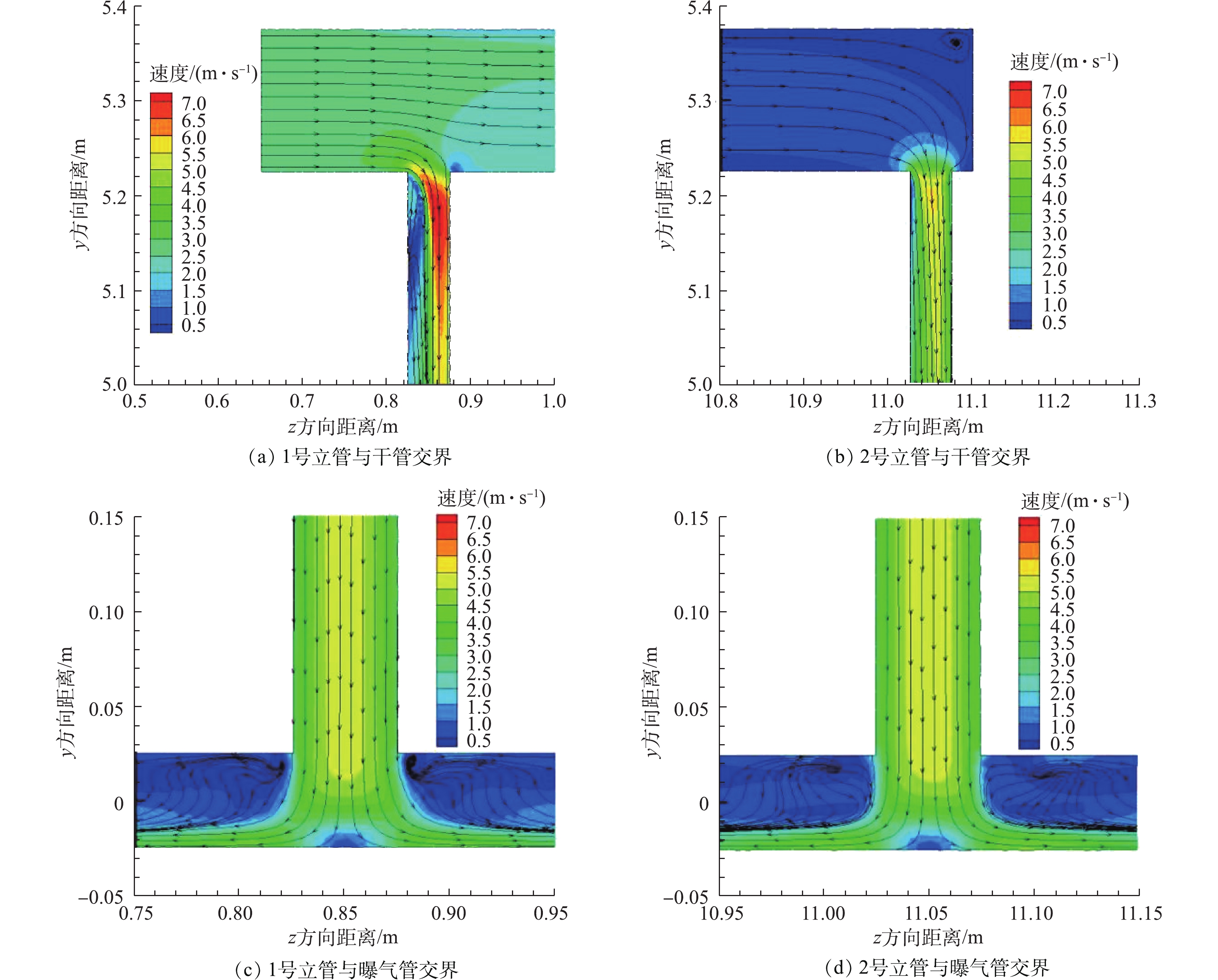
与干管进气口最近的1号立管、最远的2号立管与上部主供气干管(图4(a)和图4(b))及下部曝气管(图4(c)和图4(d))交界处的流场如图4所示。由图4可见,在接近主进气口的1号立管(图4(a))和最远的2号立管(图4(b))的流场是有很大不同的。1号立管的进气口在主干管的下游侧进气较多,而上游侧较少;2号立管的进气口则相对均匀对称,中间多,两侧较少。但在立管的下部与曝气管交界处的流场(图4(c)和图4(d)),二者却非常近似,接近于稳定管道流中的流场分布,即中间大,四周小。这可能是因为立管足够长,在流至曝气管前,使管道内的气体的流动达到了理想的稳定分布。从速度云图上看,速度的大小也是基本相同的,流量应比较接近,研究对曝气管的流量作进一步的定量检验。
-
通过Fluent软件处理,可以检查数值模拟的各管道的流量及曝气孔的曝气量,定量地分析曝气均匀性。所有6根立管的进气量以及和它们相连接的中间曝气管的3个曝气孔的曝气量如表2所示。
由表2可以看出,各立管及曝气孔的曝气量分布基本均匀,接近理论平均值。其中,各立管流量随着离进气口越远而渐渐增加,理论均值为0.008 33 m3·s−1,但标准偏差仅为4.72×10−5 m3·s−1;而曝气孔的曝气量则是离干管越远越小的趋势,但总体差别不大,理论均值为0.009 3 m3·s−1,标准偏差为7.67×10−5 m3·s−1。各立管、曝气孔间的气量相对误差较小,可认为曝气基本达到了均衡,存在的较小差别可能为实际流动的沿途压损造成的,也有可能与湍流模型、网格质量有关,下一步可通过实测来检验各立管、曝气孔间的气量相对误差。
综合以上流场及流量结果分析,可以认为该模型下的曝气达到了在各曝气管及曝气孔的流量的基本均衡。
2.1. 二维模拟结果与分析
2.2. 三维模拟结果与分析
-
1)数值模拟研究为某曝气生物滤池的曝气管道系统进行了科学的选型优化。通过二维数值模拟得出:环状曝气的4个弯道处的曝气极少;而单边枝状和中心枝状的曝气方式均匀性相对较好。
2)对原型双边枝状曝气方式三维的数值模拟显示,各曝气口的曝气量都接近均值,标准偏差为7.67×10−5 m3·s−1,故可以认为基本达到了均匀曝气。本研究可有效地助力曝气生物滤池的选型设计,以较低的成本实现高效节能的目标。


 下载:
下载: