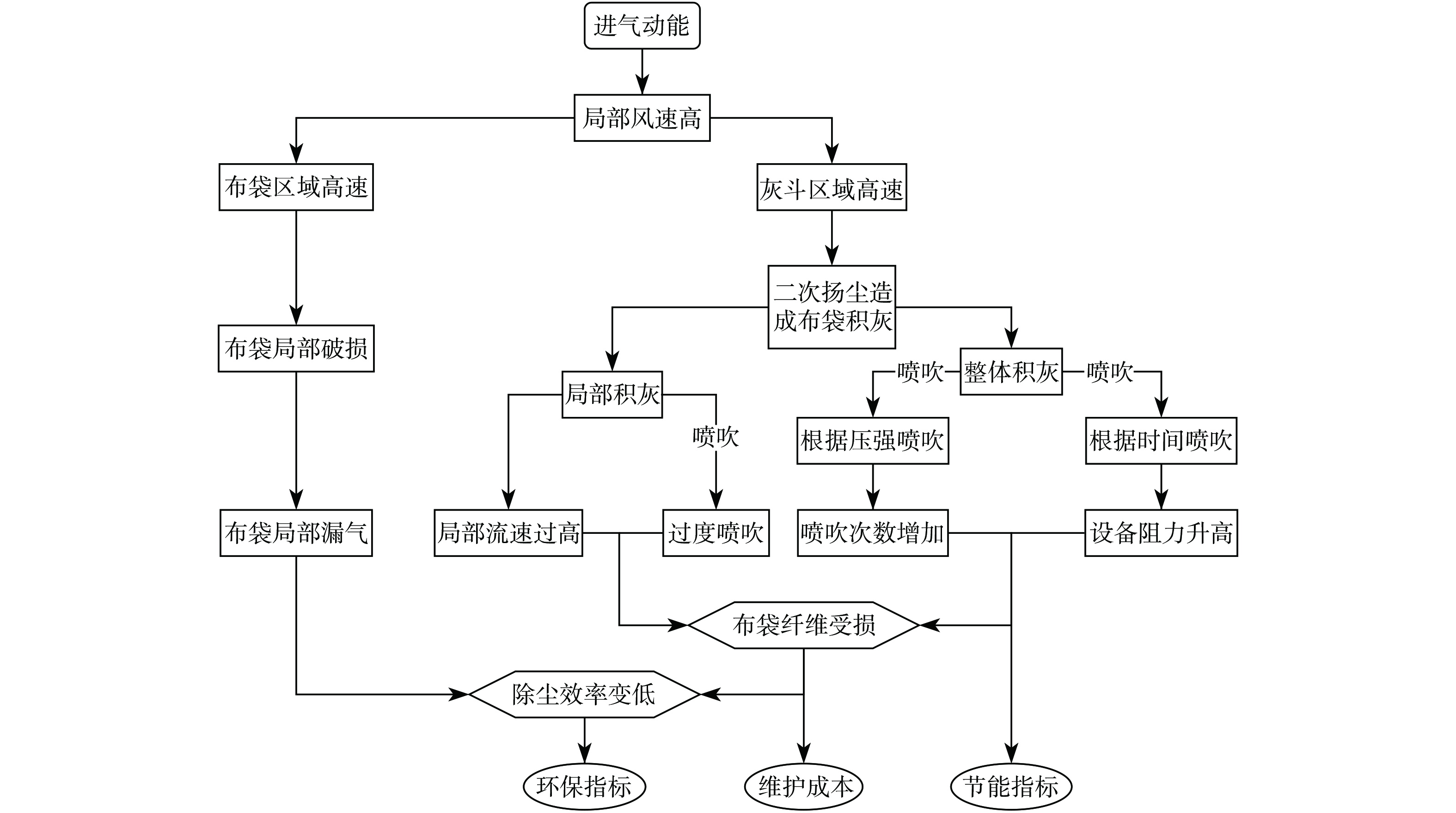
对于脉冲式布袋除尘器，在实际生产应用中，往往前期除尘效果可以达标，工作一段时间后除尘效果变差，这一般是由于布袋磨损或布袋纤维受到损伤所致。如图1所示，为进气动能对脉冲式布袋除尘器设备性能的影响。由于设备处理量确定，即出入口气体流量确定的情况下，较高的进气动能会体现为局部风速较高。首先，中箱体布袋区域较高的气体流速容易导致布袋受冲刷严重，造成布袋磨损加剧及布袋纤维受损，容易产生漏气现象和降低布袋过滤性能，从而影响除尘效率^[17]；其次，灰斗区域较高的气体流速容易导致落灰困难、布袋积灰快以及二次扬尘的产生^[18]。当布袋局部积灰明显时，使得设备阻力快速增加，导致布袋纤维容易受损，同时积灰较少的布袋气流速度升高，影响过滤性能，并导致无效喷吹次数的增加。当布袋整体积灰明显时，在根据压强设置喷吹频率的条件下，会导致设备喷吹次数增多，而喷吹次数越多布袋纤维受损越快^[19]，从而除尘效率降低；在根据时间间隔设置喷吹频率的情况下，会导致设备阻力增大，而较大的布袋内外压差会导致除尘设备能耗的明显增加，并且损伤布袋纤维，降低了布袋寿命及除尘效率^[20]。上述情况均对布袋除尘器设备性能指标有影响，并且直接关系到环保、维护和能耗的问题上。

由于布袋阻力受过滤气体流速影响明显，气体通过布袋前后存在明显的动能差异，即虽然气体到达布袋表面时具有高的气体动能，存在明显的气流分布不均匀特性，且存在大量无效流动，但气体通过布袋后无效流动明显减少，气体流动均匀性明显提高，这说明气体动能在通过布袋时被大量消耗，而这个消耗过程除了转化为内热能还会造成布袋纤维结构的损伤。与之类似的，在灰斗中过多的无效气体流动会导致灰尘颗粒沉降困难和已沉降至灰斗底部的灰尘颗粒二次扬尘，也是由于不必要的气体动能消耗造成的。这些现象的外在表现是流场气流均布差，而内在原因是较高的进气动能在不合理的区域进行的动能耗散。在脉冲式布袋除尘器结构设计过程中，若能在合理区域实现进气动能的耗散，则可以从根本上改善气流不均匀造成的不良影响。

在脉冲式布袋除尘器中动能耗散主要是湍流耗散和涡流耗散。在湍流中，由于湍流的不规则性和随机性，湍流运动导致了湍流动能的粘性耗散，并在湍流结构的各个尺度上逐渐被转化为微观的摩擦热。而高动能的流场在不同尺度上形成复杂的涡旋结构，这些涡旋由于流体粘性的存在，使得涡旋内部的速度差异逐渐减小，最终动能以热的形式被耗散。

根据湍动能公式如式(1)所示。

式中：$k$为湍动能，m²·s⁻²；$v$为平均速度，m·s⁻¹；$I$为湍流强度。

根据湍流强度公式如式(2)所示。

式中：$Re$为雷诺数。

根据运动粘度公式如式(3)所示。

式中：$\nu $为运动粘度，m²·s⁻¹；$\mu $为动力粘度，Pa·s；$\rho $为密度，kg·m⁻³。

其中雷诺数公式如式(4)所示^[21]。

式中：$L$为湍流尺度 ($L$越小，湍流强度越大) ，m；$\varepsilon $为湍流耗散率。

将式(1)、(2)、(3)代入式(4)可得湍流耗散率公式，如式(5)所示。

湍流耗散率是描述流体运动中动能转化的重要参数，它表示单位时间内单位体积流体的动能被转化为内能的速率。由此可得出单位时间内湍流动能耗散${E_1}$的关系式，如公式(6)所示。

式中：${E_1}$为湍流动能耗散，J；$V$为体积，m³。

涡度是一个矢量，即速度场的旋度，如式(7)所示。

式中：$ {{\Omega }} $为涡度，s⁻¹；$\vec v$是速度矢量，m·s⁻¹。

单位时间内涡流动能耗散${E_2}$的关系式^[22]，如式(8)所示。

式中：${E_2}$为涡流动能耗散，J；$\mu $为动力粘度，Pa·s；$V$为体积，m³。

由式(6)和式(8)可得出在单位时间内总的动能耗散$ E $，如式(9)所示。

通过公式(9)可知，在特定的流场环境下，流体的密度与动力粘度一定，动能耗散的多少与湍流速度、涡流速度、耗散体积成正相关；而与湍流尺度成负相关，当湍流尺度越小时，湍流强度越大，动能耗散越多。

因此对于脉冲式布袋除尘器合理的流场应具备以下特征：1) 避免在灰斗和布袋区域内进行动能的大量的耗散 (产生原因气体动能过高) ；2) 灰斗区域低流速，特别是灰斗底部附近；3) 布袋区域流速低且分布均匀。

为了符合数学模型获得的流场特性需求，在设计脉冲式布袋除尘器时应尽可能避免湍流和涡流对重点区域的影响，而气体动能以湍流和涡流的形式在进气道区域耗散并不会对灰斗底部和布袋区域造成过多的影响，因此，本研究中设计了耗散箱的结构，力求在进气道区域最大化地实现气体动能耗散，相应地减少灰斗底部及布袋区域的气体动能，进而实现合理的动能耗散规划。

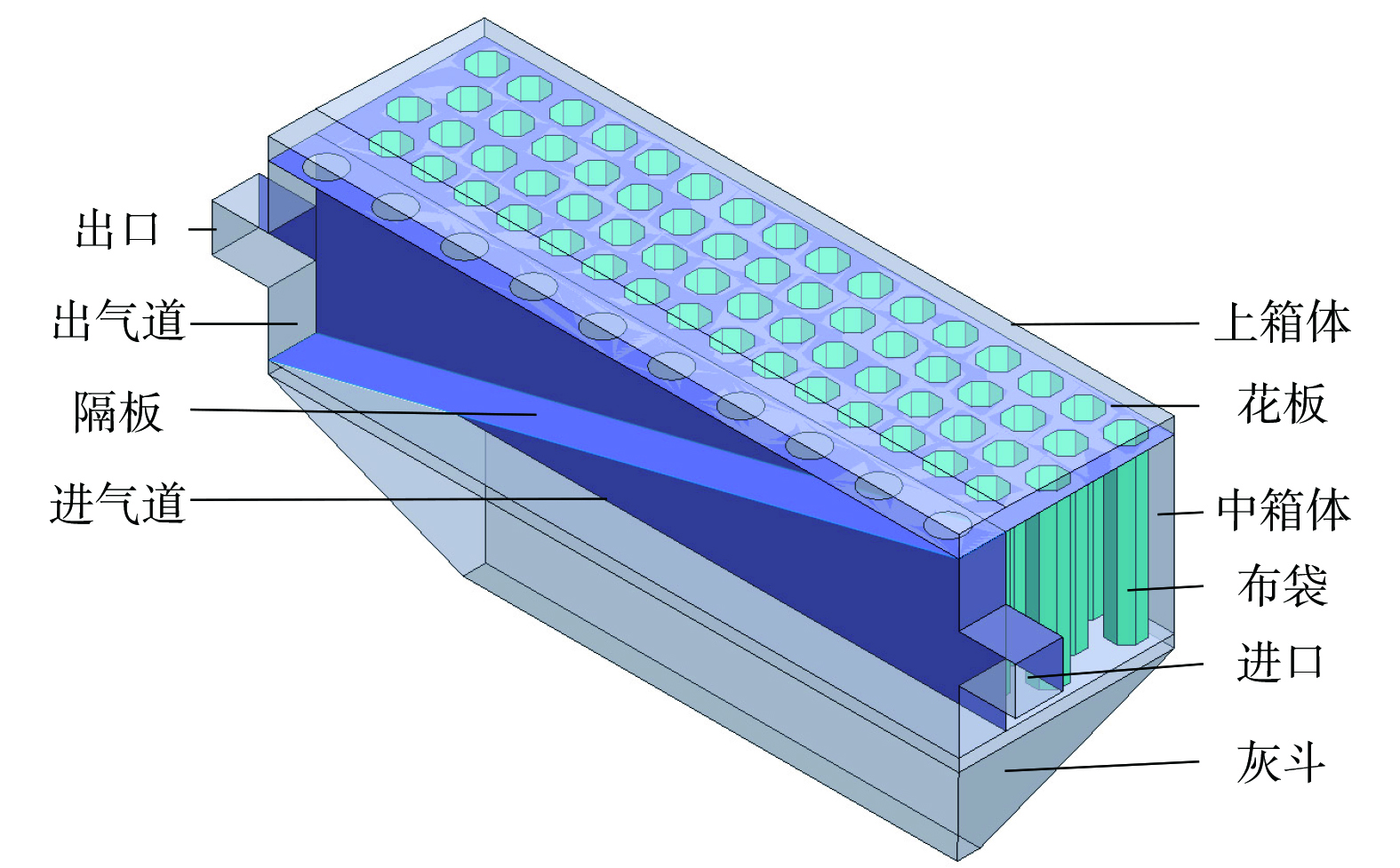
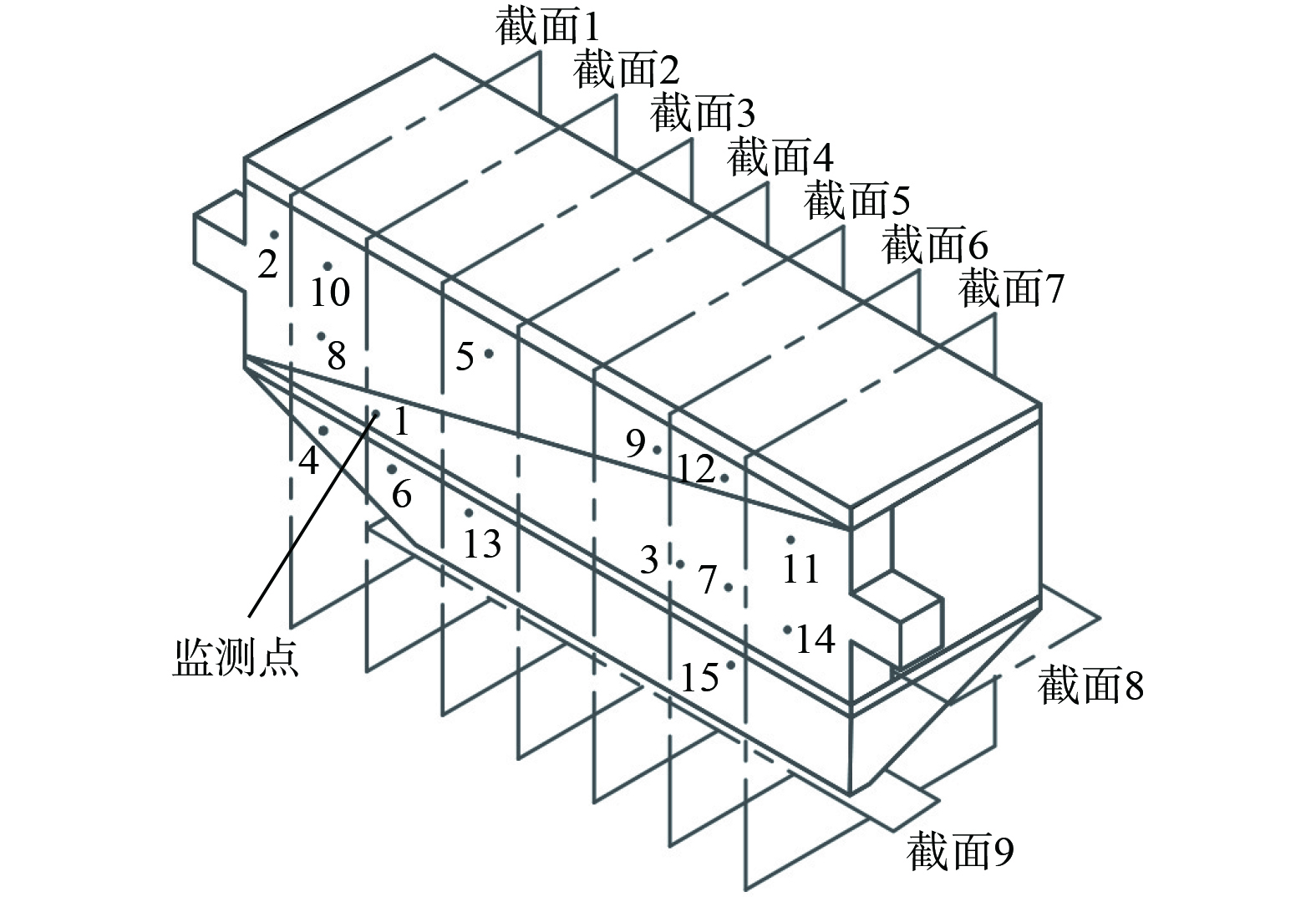
参照脉冲式布袋除尘器实物，利用SolidWorks对布袋除尘进行简化仿真模型的建立，所建模型如图2所示。若按实际布袋数量进行多孔阶跃界面的设置对仿真时间影响极大，为了提高运算效率，在确保仿真结果准确的情况下对布袋进行简化处理，将原始规格为Φ130 mm×3 060 mm，数量为1 280条，简化为Φ580 mm×3 060 mm，数量为62条，简化原则为花板开孔面积占比与真实模型一致。其中，中箱体尺寸为12 150 mm×2 970 mm×3 060 mm；进气道和出气道是由尺寸为12 150 mm×830 mm×3 060mm长方体用隔板从斜对角分隔而成；灰斗高为3 283 mm，排灰口长宽为8 700 mm×400 mm；上箱体尺寸为12 150 mm×3 800 mm×375 mm；进出气口截面为830 mm×830 mm。为后续分析方便选取如图3所示的截面与监测点。

本研究主要针对进气道进行改进，在进气道前增加一个耗散箱结构，并在进气道内添加一定数量大小的弧形导流板和“V”形挡板。如图4所示的2种不同的进气道模型，图4(a)为原始进气道模型，图4(b)为改进后的进气道模型。

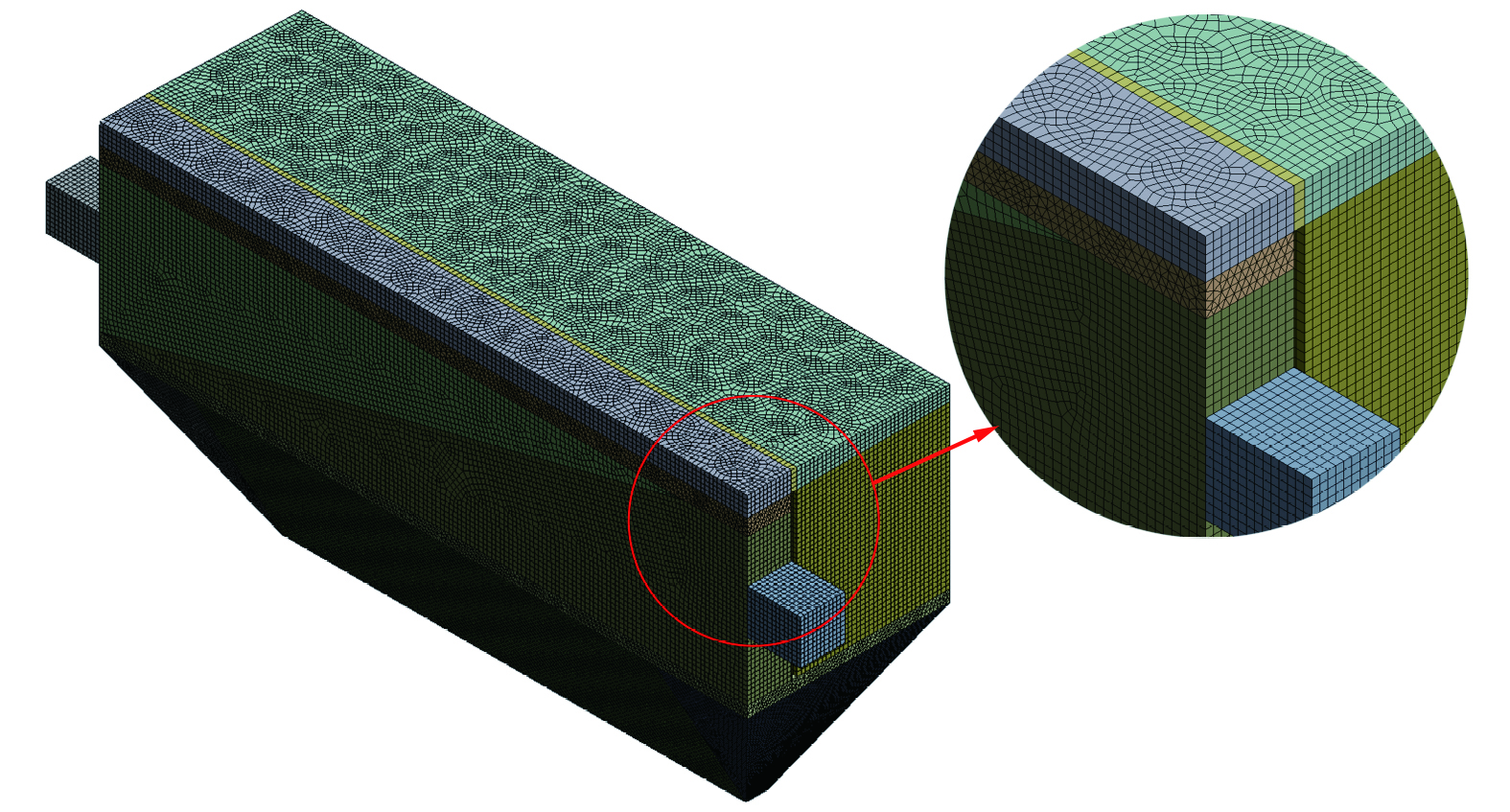
在确保网格质量最好的情况下，通过Mesh对脉冲式布袋除尘器仿真模型进行分块分区域使用不同的网格划分方法，采用结构化与非结构化的形式对其进行网格划分，并且大多区域为六面体网格，如图5所示。

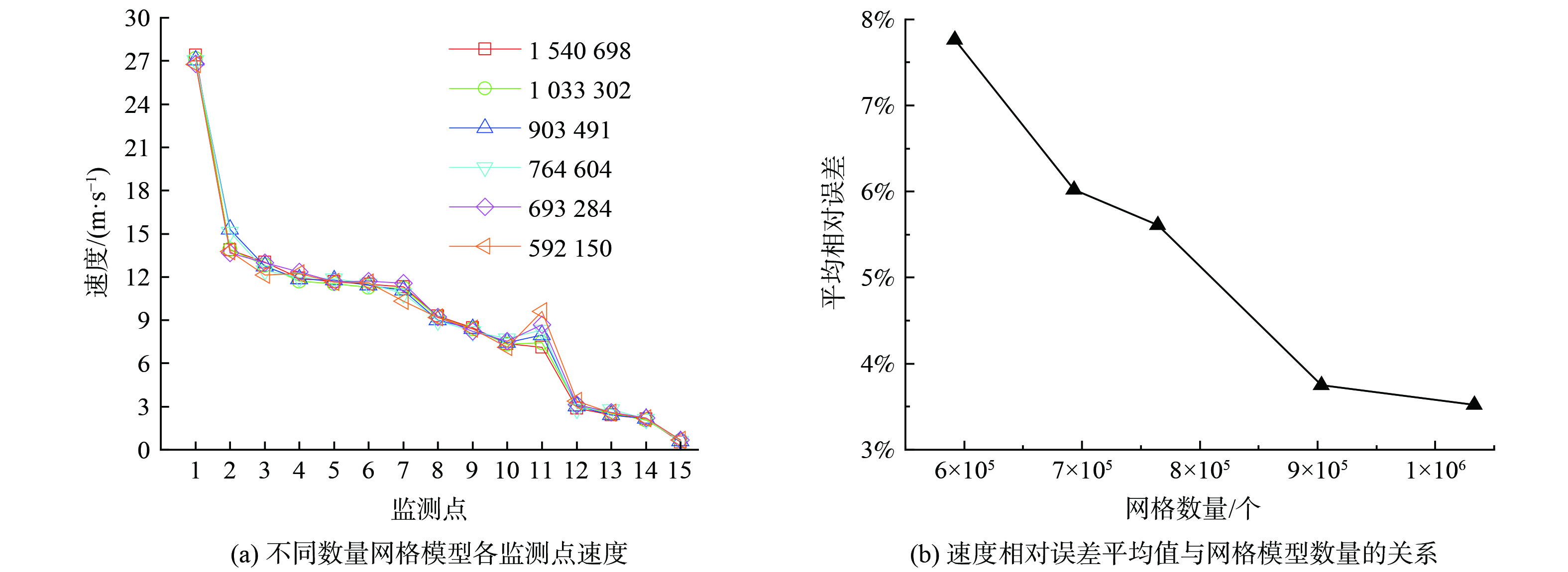
网格无关性验证是指在模型划分不同数量网格下，对数值模拟结果的准确性进行评估。即采用网格逐步加密方法对不同数量的网格模型进行模拟，比较所得结果的差异，确定最少网格模型下的收敛解。若在不同数量网格下得到的计算结果趋近于某一值，则认为该模型的结果具有网格无关性。对脉冲式布袋除尘器模型分别选取592 150、693 284、764 604、903 491、1 033 302和1 540 698个网格进行模拟仿真。在布袋除尘器内选取15个监测点，如图3所示。并统计每个监测点的速度值，结果如图6(a)所示。通过对不同数量网格模型下的15个监测点速度求相对误差，并对这些监测点的速度相对误差求均值，得到速度相对误差平均值与网格模型数量的关系，如图6(b)所示。当网格数量为903 491个时，速度相对误差平均值为3.75%，结果的准确性较高，说明此时已通过无关验证，因此选用903 491个网格对模型进行划分。

多孔阶跃模型是多孔介质模型的一维简化模型，是将多孔介质视为由多种均匀分布且不同的材料组成的分层结构，可用于模拟具有已知压降速度特性的薄膜介质，相对多孔介质模型来说更容易收敛。主要是把薄膜介质的压力改变视为附加的内部损失项和Darcy定律的结合^[23]，压降方程如式(10)所示。

式中：$\Delta p$为压力损失，Pa；$ \mu $为流体动力粘性系数，Pa·s；$ \alpha $为渗透率，m²；$ v $为垂直于过滤介质表面的速度分量，m·s⁻¹；${C_2}$为压力跃变系数；$ \rho $为流体密度，kg·m⁻³；$ \Delta m $为多孔介质厚度，m。

布袋为多孔介质，因此采用多孔阶跃模型来定义布袋边界条件。由于压力损失主要为粘性损失，可忽略第二项内部阻力^[24]。该结论与布袋阻力经验公式一致^[25]，如式(11)所示。

式中：$\Delta P$为布袋阻力，Pa；$\mu $为流体动力粘性系数，Pa·s；$v$为气体速度，m·s⁻¹；$L$为滤料厚度，m；$d$为纤维直径，m；$Re$为雷诺数；$k$为压降系数。

因此通过设定渗透率$ \alpha $和多孔介质厚度$ \Delta m $参数来实现布袋边界条件设定。空气动力粘性系数为1.79×10⁻⁵ Pa·s，多孔介质厚度0.002 m，渗透率为2.148×10⁻¹² m²。

离散相 (DPM) 是一种用于模拟颗粒物运动的模型，它是基于拉格朗日方法，通过追踪大量离散颗粒的运动来模拟颗粒物在流场中的行为。颗粒运动方程为是根据牛顿第二定律在拉格朗日坐标下得出^[26]，颗粒作用力平衡方程如式(12)~式(13)所示。

式中：$\overrightarrow {{u_p}} $为颗粒流速，m·s⁻¹；$\overrightarrow {{F_C}} $为碰撞作用力，N；$\overrightarrow {{F_D}} $为曳力，N；$\overrightarrow {{F_G}} $为重力，N；$\overrightarrow {{F_M}} $为马格努斯升力，N；$\overrightarrow {{F_O}} $为其它外力，N；$\overrightarrow {{F_p}} $为压力梯度力，N；$\overrightarrow {{F_{VM}}} $为虚质量力，N；${I_P}$为颗粒转动惯量，kg·m²；${m_p}$为颗粒质量，kg；$\overrightarrow {{T_C}} $为颗粒碰撞产生的力矩，N·m；$\overrightarrow {{T_{RD}}} $颗粒旋转产生的力矩，N·m。

DPM适用于颗粒相体积分数小于10%，不考虑颗粒本身的体积，也不考虑颗粒之间的作用力，但考虑流体与颗粒间的作用力^[27]，颗粒主要受气流曳力和重力的影响^[28]。对于脉冲式布袋除尘器来说含尘气体颗粒体积分数远小于10%，因此可采用DPM进行模拟。

利用Fluent对脉冲式布袋除尘器进行模拟仿真，将布袋除尘器内部视为常温常压下不可压缩气体，按照最大处理风量为70 000 m³·h⁻¹进行，其模拟相关仿真参数设置如表1所示。

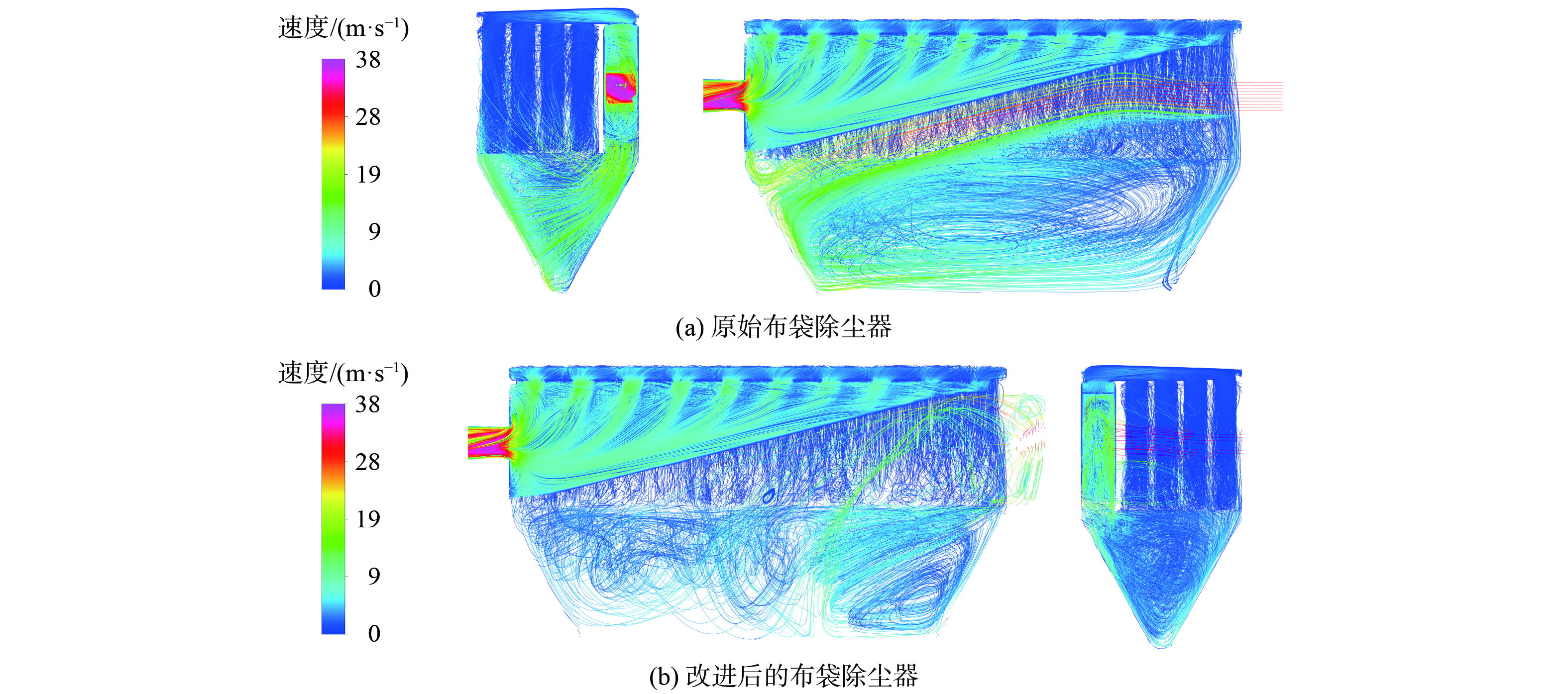
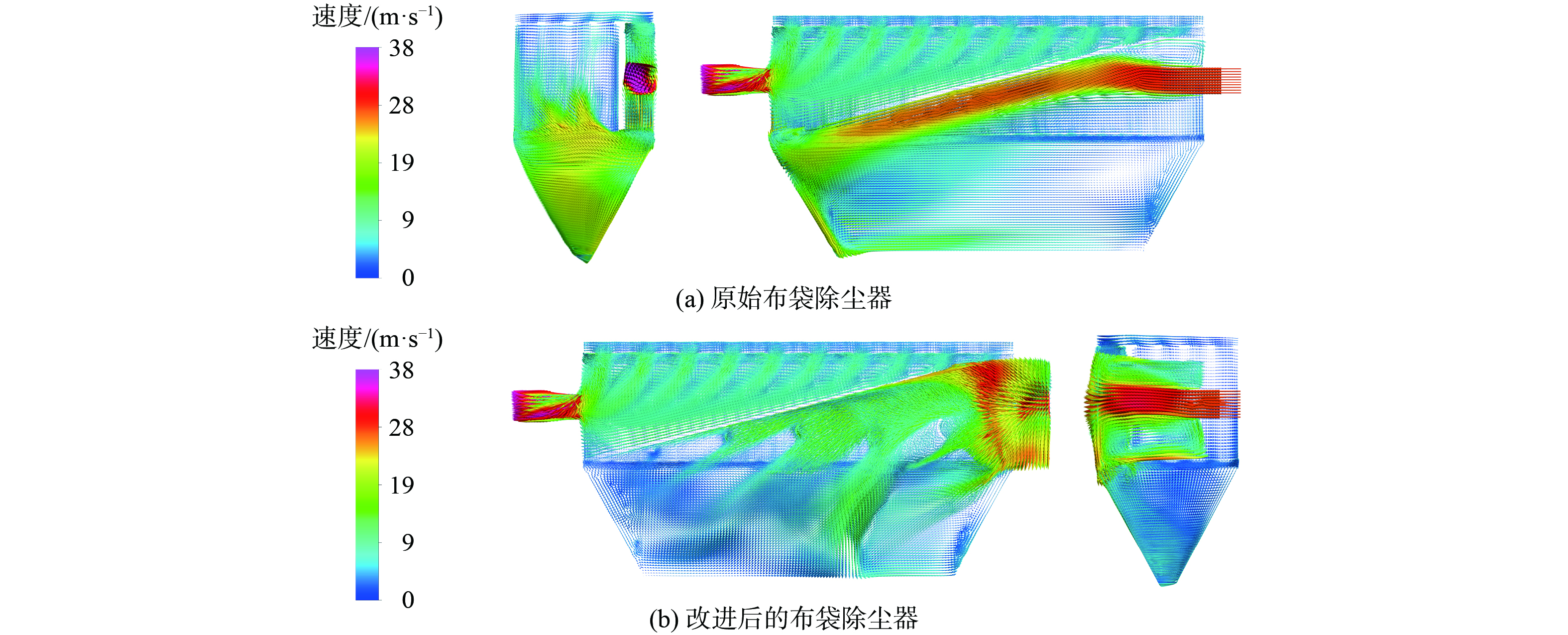
如图7和图8所示，分别为原始脉冲式布袋除尘器与改进后的脉冲式布袋除尘器的迹线图和速度矢量图。

对于原始布袋除尘器，入口气流以射流形式冲击到隔板上；之后继续以射流形式沿着隔板平行运动，冲击到灰斗侧壁。此时大量高速气流在射流通道中运动，气体流速较大，动能消耗较低，含尘气体仍具有较高的动能。高速气流在灰斗侧壁的阻碍下转向，一部分高速气流流向中箱体中的布袋区域，受到布袋的阻碍后动能逐步消耗，此时布袋底部及中箱体侧壁均存在明显的高速气流，大量气体动能作用于布袋表面，导致布袋的磨损及纤维的损伤，从而影响布袋的使用寿命；另一部分气体在灰斗侧壁的引导下向下流入灰斗中及灰斗底部，在灰斗中形成了大的漩涡，并且气流速度较高，导致布袋区域灰尘沉降困难以及灰斗底部灰尘的二次扬尘。

改进后的布袋除尘器很好地改善了上述问题，入口气流在耗散箱内被分成上下两股，并分别形成了顺时针和逆时针涡旋。根据公式(9)可知，该高速涡旋可以提前通过涡流和湍流的耗散实现进气动能的消耗，使得含尘气体进入进气道后的动能降低。耗散箱流出的含尘气体经弧形导流板和“V”形挡板引导后，在进气道实现进一步均匀扩散，而分散气流与周围气体之间形成明显速度梯度，并产生大量低速涡流和湍流，进一步实现了气体动能消耗。当气流到达灰斗中及灰斗底部时，气体动能明显降低，无效气体流动减少。虽然在灰斗中形成了三个小的漩涡，但它们的速度相对较低，对灰尘颗粒的沉降和二次扬尘的产生影响较小。

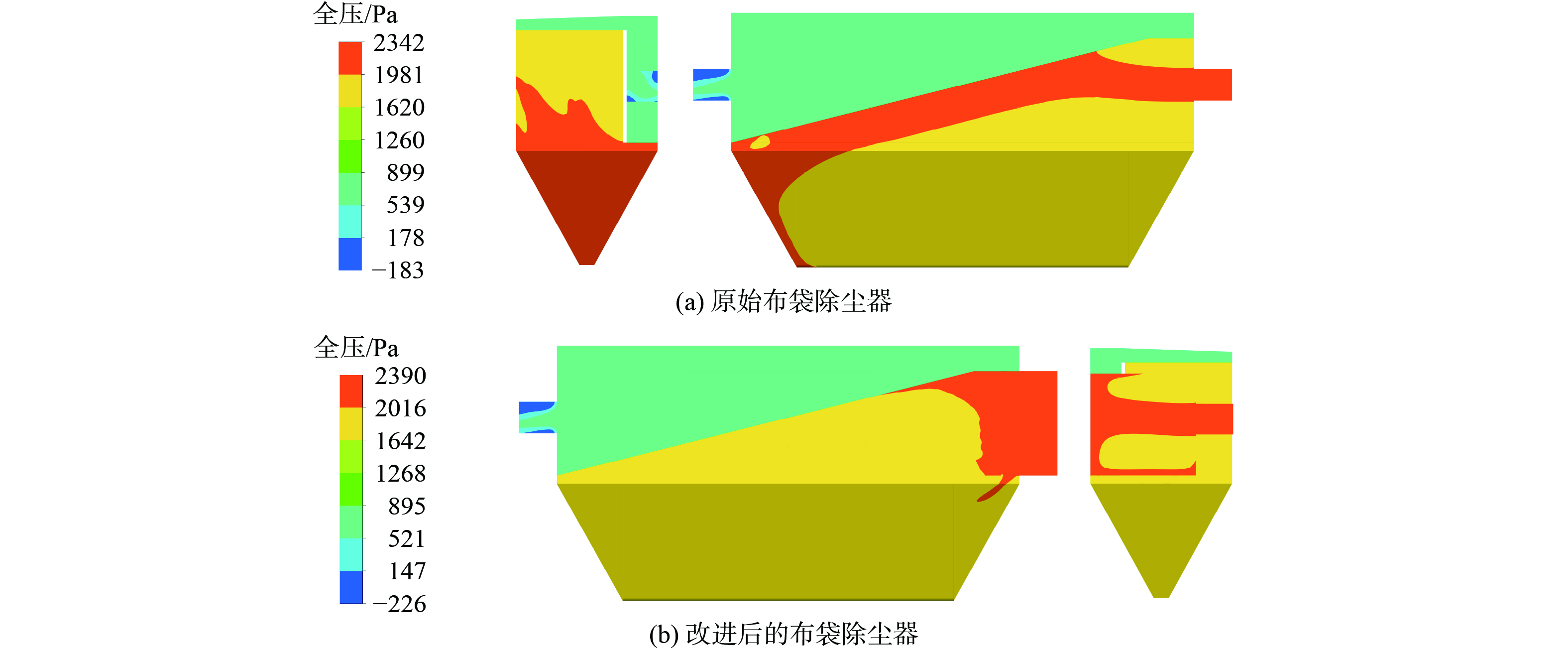
如图9所示，为原始脉冲式布袋除尘器和改进后的脉冲式布袋除尘器全压云图。原始布袋除尘器全压较高的区域主要集中在进气道、灰斗左侧和中箱体左侧，改进后的布袋除尘器全压较高的地方主要集中在耗散箱中，高全压区均为高气体流速区域。对于改进前后的布袋除尘器，当进气动能一定时，原始布袋除尘器入口全压为2 342 Pa，改进后的布袋除尘器入口全压为2 390 Pa，改进后的布袋除尘器比原始布袋除尘器全压高了48 Pa，其差值仅为2%。

布袋除尘器出入口全压压差即为设备压力损失，如式(14)所示，该参数与布袋除尘器内含尘气体所获得的气体动能有关。

式中：$E$为气体动能，J；$P$为全压，Pa；$V$气体体积，m³。

气体通过布袋后，在上箱体和出气道的流场中，原始布袋除尘器和改进后的布袋除尘器没有本质差异。根据公式(11)可知，对于改进前后的布袋除尘器，$\mu $、$L$、$d$、$Re$、$k$参数一样，布袋阻力与气流速度$v$成正相关，当气体流速在垂直布袋表面方向上具有较高分量时，布袋的阻力较大；反之，布袋的阻力较小。布袋阻力大的区域的气流向布袋阻力小的区域流动，最终实现气流以相对均匀的气速穿过布袋，通过布袋后气体速度均匀性明显提高。

由于改进前后布袋除尘器进口流量相同，且过滤界面特性相同，由式(11)可得出式(15)的关系式，改进前后气流通过布袋的速度与布袋的压力损失成正比。因为改进前后气流通过布袋时损失的$ \Delta {p_1} $、$ \Delta {p_2} $压力范围在−100~100 Pa之间，远小于通过布袋时的理论平均压力损失p=1 000 Pa，所以$ \dfrac{{\Delta {p_1} - \Delta {p_2}}}{{p+\Delta {p_2}}} $的值趋于很小。因此认为改进前后的布袋除尘器在气流通过布袋后的速度基本相同。并且上箱体和出气道的结构也相同，气流通过布袋后的流场也就基本一致，因此认为残余的气体动能是相同的。

式中：$ {v_1} $、$ {v_2} $为改进前后气流通过布袋的速度，m·s⁻¹；$ p $为通过布袋时的理论平均压力损失，Pa；$ \Delta {p_1} $、$ \Delta {p_2} $为改进前后气流通过布袋时的压力损失与理论压力损失差值，Pa。

对于改进前后的布袋除尘器，气体进口流量一致，说明进入布袋除尘器的含尘气体从引风机所获得的气体动能${E_z}$一致。为了更好地了解进气动能的消耗过程，将${E_z}$分为不同区域进气动能消耗和残余气体动能之和，即：进入进气道阶段消耗的动能${E_1}$、在灰斗和中箱体及布袋表面消耗的动能${E_2}$、通过布袋时消耗的动能${E_3}$和残余气体的动能${E_4}$，为此可得进入布袋除尘器的动能${E_z}$的关系式，如式(16)所示。

改进前后的布袋除尘器${E_z}$、${E_3}$和${E_4}$一致，则${E_1}+{E_2}$为定值，当${E_1}$消耗较少时，在灰斗和中箱体及布袋表面的气体动能消耗${E_2}$大幅度增加，从而导致布袋使用寿的降低、落灰困难和二次扬尘的产生。而对于改进后的布袋除尘器，由于耗散箱的存在，${E_1}$的消耗更大，相应地${E_2}$动能消耗降低，使得上述问题得到改善。

如图10所示，为原始脉冲式布袋除尘器和改进后的脉冲式布袋除尘器在距灰斗底部上方相同位置所截取的速度云图，所选取的位置如图3的截面9所示。可以看出原始布袋除尘器灰斗底部局部区域最高风速达到了19.2 m·s⁻¹，这是由于大量高速气流沿着进气道隔板直接冲到了灰斗中所造成的；其余大部分区域在9 m·s⁻¹左右。而改进后的布袋除尘器灰斗底部最高风速为9.6 m·s⁻¹，并且风速相对均匀。由此可见，布袋除尘器增加耗散箱结构后，在灰斗底部气体动能明显降低，更有利于灰尘颗粒的沉降和减少二次扬尘的产生。

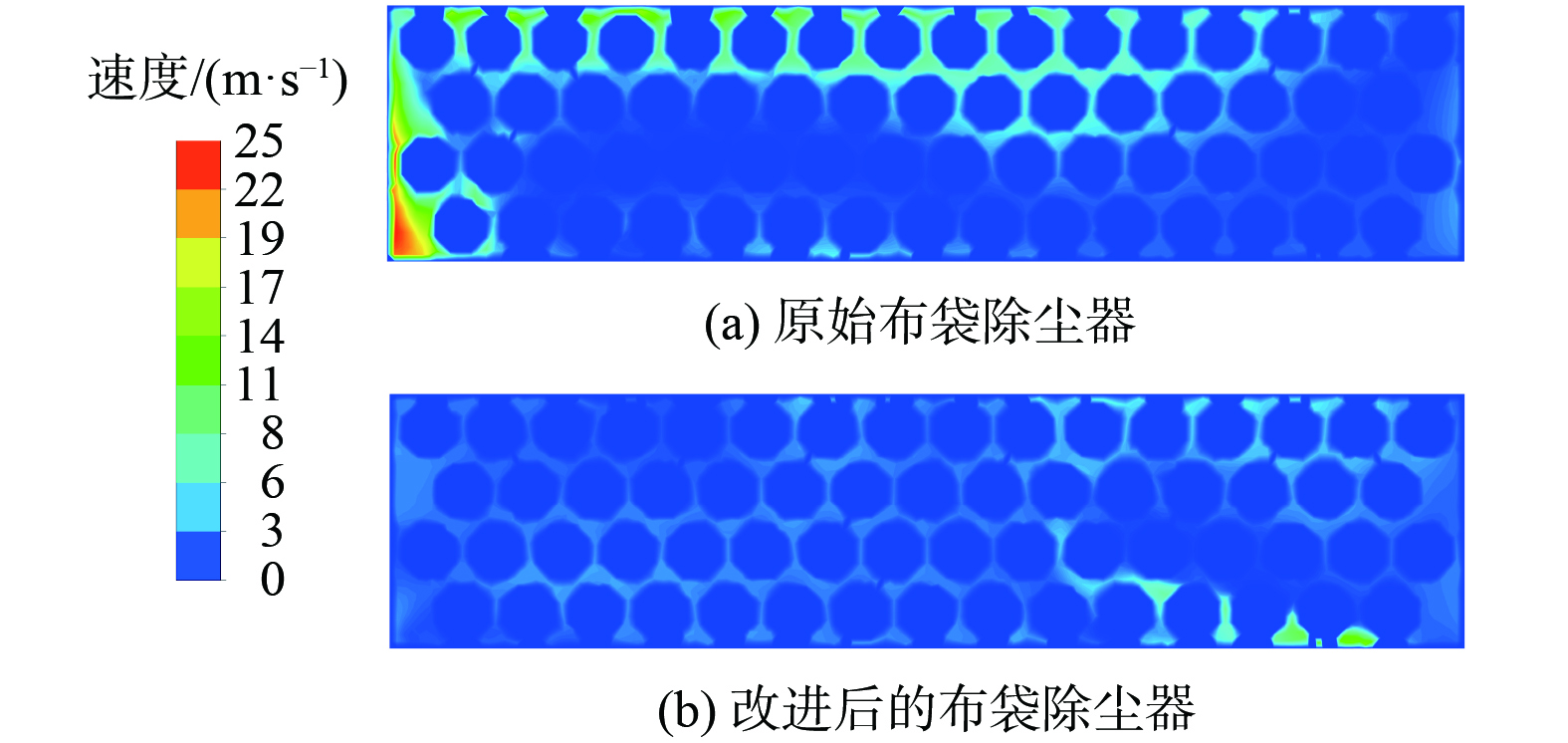
如图11所示，为原始脉冲式布袋除尘器和改进后的脉冲式布袋除尘器在靠近中箱体底部上方相同位置所截取的速度的云图，所选取的位置如图3的截面8所示。原始布袋除尘器中箱体上方与左侧区域的布袋周围风速较高，最高风速达到24.4 m·s⁻¹，对布袋的冲刷尤为严重，使得此处的布袋纤维容易损伤及破损加快，这也是除尘效率降低的原因。改进后的布袋除尘器中箱体中布袋周围的最高风速仅为9.3 m·s⁻¹，并且中箱体中的风速分布相对均匀。由此可见，布袋除尘器增加耗散箱结构后，在中箱体底部气体动能明显降低，大幅度减轻对布袋的冲刷及损伤，从而提高了布袋的使用寿命，延长维护保养周期。

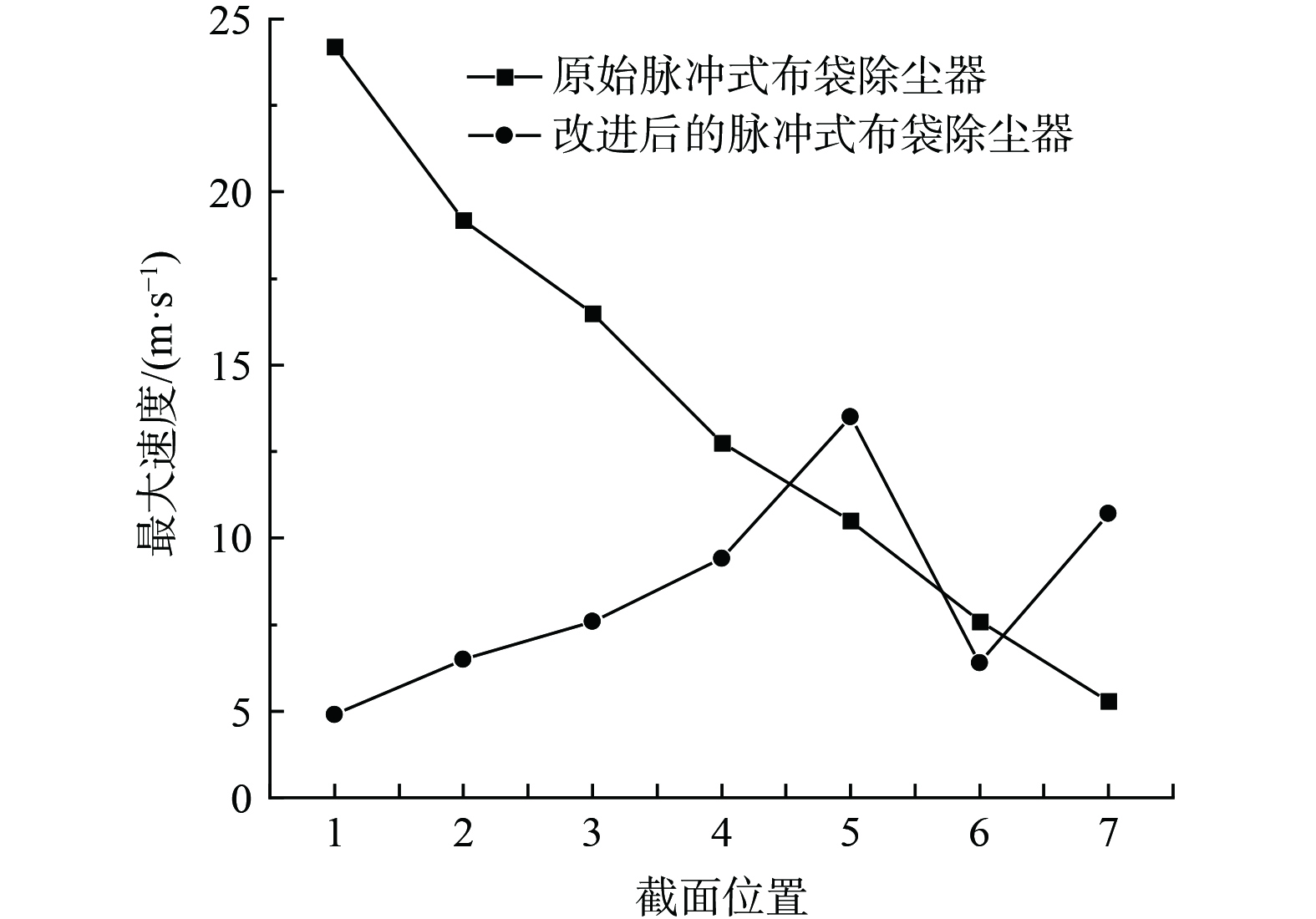
分别在原始脉冲式布袋除尘器和改进后的脉冲式布袋除尘器主体纵向上从出口端向进口端依次等间距截取7个截面，所截取的截面1至截面7如图3所示。改进前后的脉冲式布袋除尘器各截面上的最大速度值如图12所示。

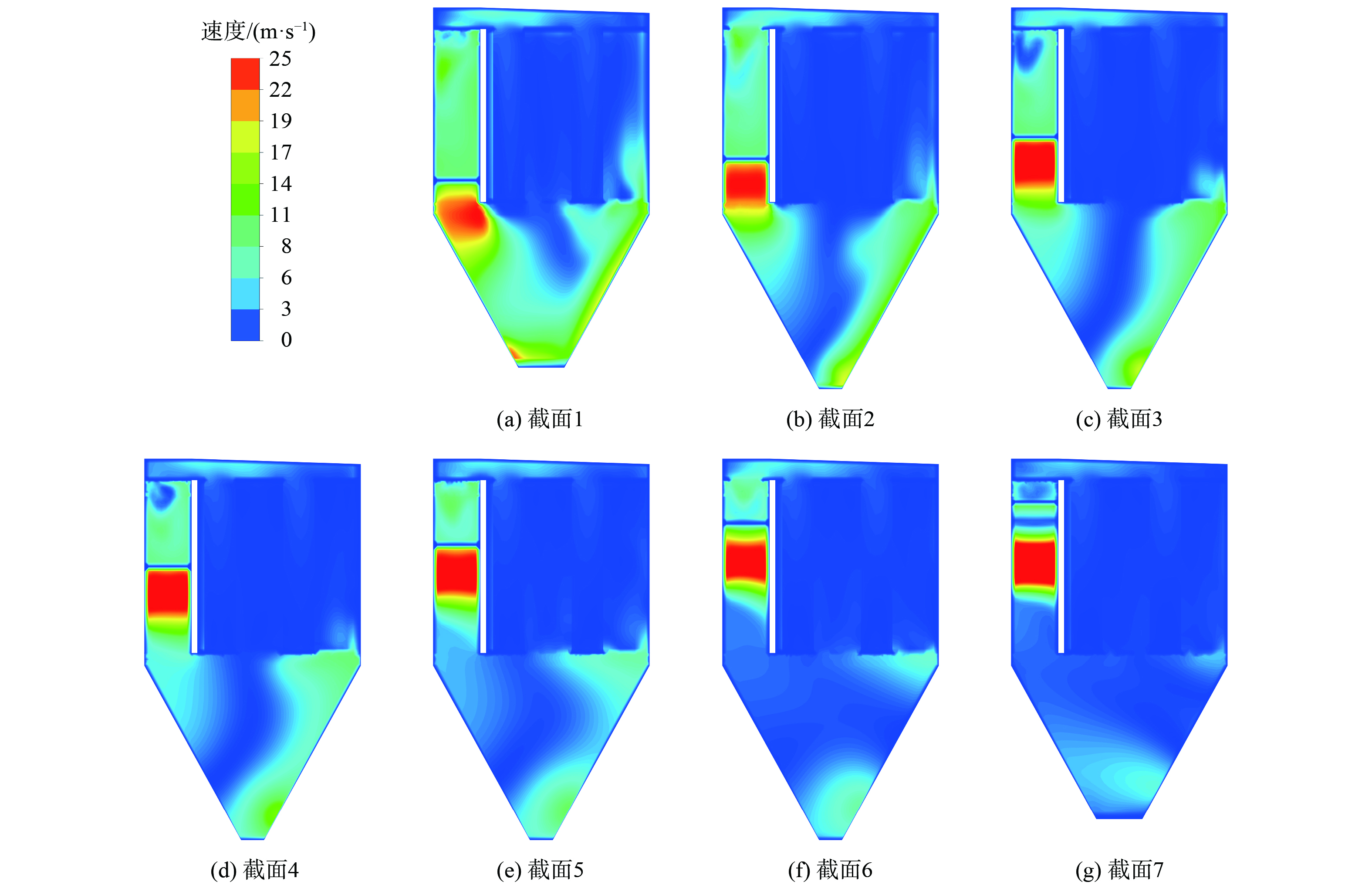
如图13所示，(a)~(g)为原始布袋除尘器上截取的速度云图。在灰斗左上角、右上角、右侧及灰斗底部均有高速区存在。其中，灰斗左上角高速区是由于流入的气体大部分从进气道末端流向灰斗中，对截面1前的布袋区域造成严重影响，会导致布袋提前破损，对截面2到截面7的局部区域上的布袋也会造成一定影响；灰斗右上角高速区是由于高速气流沿着灰斗右侧壁流动并向布袋区域扩散，导致局部布袋寿命降低；灰斗底部高速区域会造成落灰困难和二次扬尘的产生。同时截面1中，灰斗区域存在大面积高速区域，速度为12.4~21.8 m·s⁻¹，这也在灰斗中产生高速漩涡的原因。

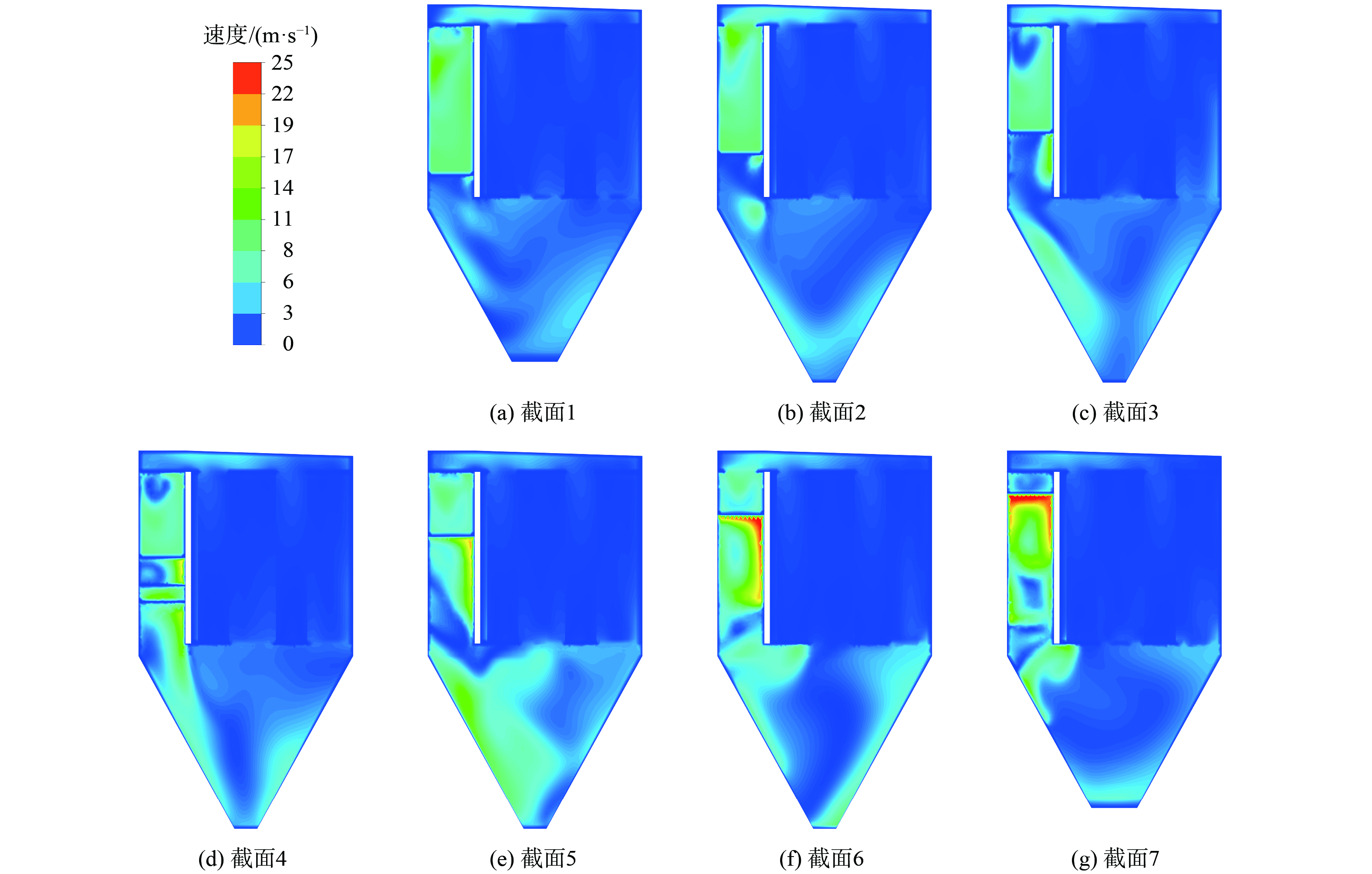
如图14所示，(a)~(g)为改进后的布袋除尘器上截取的速度云图。虽然在截面5和截面7存在气体流速相对较高的区域，但都集中在灰斗左侧区域，并不会对布袋区域和落灰造成显著影响。灰斗底部区域的速度低于9.6 m·s⁻¹，与原始布袋除尘器相比，气体流速明显降低，减少了进气动能在布袋区域与灰斗区域的消耗，提高了布袋的使用寿命及灰尘的沉降效率并减少了二次扬尘的产生。

为了解不同进气道结构条件下的动能耗散对灰尘颗粒沉降效率的影响，采用DPM法进行颗粒运动分析，同时注入粒径为25、50、75、100、150、200、250和300 μm的颗粒来模拟实际含尘气体的运动情况，颗粒注入时间0.1 s，仿真运算时间为30 s。如表2所示为颗粒在不同区域分布占比。改进前后的布袋除尘器在中箱体区域各种粒径颗粒数量占比均小于2.5%，说明绝大部分颗粒完成了沉降或被布袋捕获，即30 s仿真运算时间为有效时长。

对于75 μm以下的颗粒，有耗散箱结构的布袋除尘器在灰斗里颗粒数量占比高于原始布袋除尘器，体现出一定优势。由于颗粒在空气中主要受到曳力和重力等的影响，在粒径较小时，颗粒受重力影响较小，而受空气运动影响显著，因而两者均仅有极少的颗粒沉降在灰斗里，这些颗粒只能通过被布袋捕获团聚成团后，再经喷吹清灰落入灰斗中。对于100 μm以上的颗粒，原始布袋除尘器中布袋捕获占比明显高于改进后的布袋除尘器，造成上述现象的主要原因是由于进气动能在灰斗中消耗，产生了湍流和涡流，不利于落灰并易造成二次扬尘的产生，从而导致了布袋捕获颗粒数量的增加，在实际操作过程中，必须提高喷吹频率以保障操作压力，而过多的喷吹次数会导致布袋纤维受损，降低布袋寿命；改进后的布袋除尘器中100~300 μm的颗粒沉降效率远大于原始布袋除尘器，尤其是大颗粒沉降在灰斗里的占比达到了90%以上，仅有极少数被布袋捕获，这说明进气动能在进气道前大量消耗，气体流入灰斗后无效流动减少，动能降低，提高了灰尘颗粒的沉降能力，同时也提高了被布袋捕获团聚后清灰下来的灰尘颗粒沉降能力。由此可见合理地消耗进气动能有利于灰尘颗粒的沉降和延长布袋的使用寿命。

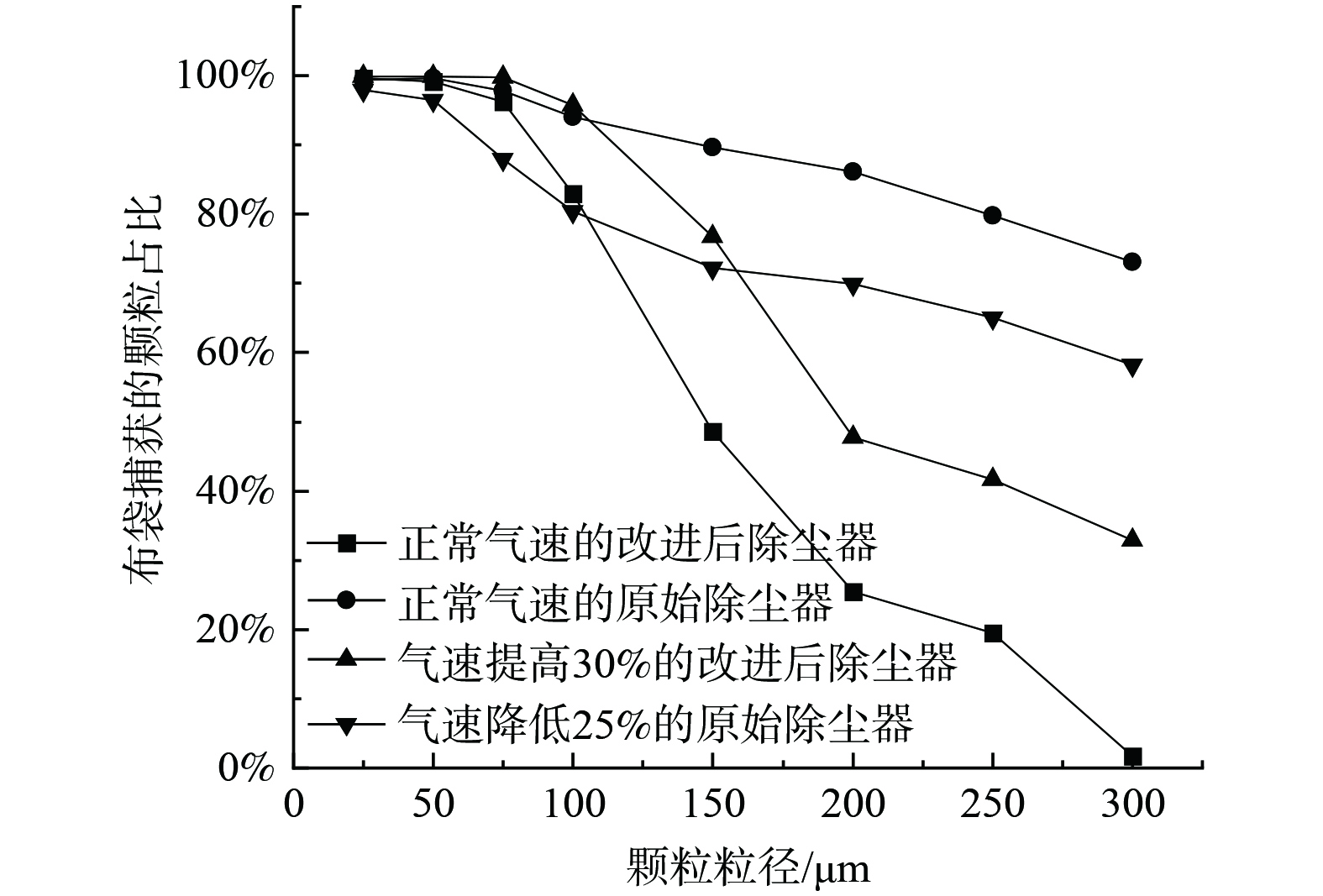
此外，为了更好地通过仿真结果表征改进前后的布袋除尘器性能差异，对改进后的布袋除尘器进气速度提高30%和原始布袋除尘器进气速度降低25%与正常进气速度原始布袋除尘器和正常进气速度改进后的布袋除尘器在布袋区域对不同颗粒捕获数量占各总输入量的比值进行对比分析，结果如图15所示。

对于25~75 μm的颗粒，气速提高30%的改进后布袋除尘器与正常进气速的原始布袋除尘器相比，气速提高30%的改进后布袋除尘器的布袋对小颗粒捕获占比要稍高于正常气速的原始布袋除尘器，这也是由于粒径较小时，颗粒受空气运动影响显著，只能被布袋捕获团聚成团后，通过喷吹落下并沉降到灰斗里；对于100~300 μm的颗粒，正常进气速的原始布袋除尘器的布袋对颗粒捕获占比远大于气速提高30%的改进后布袋除尘器。由此可见，改进后的布袋除尘器即使提高进气速度，布袋对颗粒的捕获占比也少于正常进气速度的原始布袋除尘器，这说明耗散箱结构可以提前消耗进气动能，并且对灰尘颗粒沉降是有利的。

正常气速的改进后布袋除尘器与气速降低25%的原始布袋除尘器相比，对于25~75 μm的颗粒，气速降低25%的原始布袋除尘器的布袋对颗粒的捕获占比要略少，而对于100~300 μm的颗粒，正常气速的改进后布袋除尘器的布袋对颗粒的捕获占比明显降低。虽然原始布袋除尘器降低进气速度减少了较小颗粒被布袋捕获的占比，但对于较大颗粒来说，正常气速的改进后布袋除尘器被布袋捕获的颗粒占比要更少。改进后的布袋除尘器不仅可以提高大颗粒沉降效率，也提高了清灰落下的团聚颗粒沉降效率，相比而言，改进后的布袋除尘器具有更明显优势。

综上所述，相对于原始布袋除尘器，改进后的布袋除尘器即使在提高进气速度30%的情况下，在大粒径灰尘颗粒上仍然具有明显的沉降优势；反之，原始布袋除尘器即使降低进气速度25%也不能达到同等水平的颗粒沉降率。由于颗粒具有团聚特性，小颗粒被布袋捕获后可团聚为大颗粒，会获得更好的沉降能力，与降低原始布袋除尘器进气速度相比，改进后的布袋除尘器对颗粒的沉降效果会更好，能减少二次扬尘的产生，也提高了清灰下来的团聚颗粒沉降效率，减少了布袋喷吹清灰频率，从而减少因喷吹次数过多造成的布袋损坏。

1) 脉冲式布袋除尘器除尘效果变差的主要原因是布袋受损所致，造成布袋使用寿命降低的主要原因是布袋区域与灰斗区域流速过高，过高的气流速度会引起湍流和涡流的产生，造成了动能在中箱体和灰斗中的消耗，均为不必要的气体动能消耗，从而导致了二次扬尘的产生和加快布袋的破损。

2) 通过数学模型分析得出，动能耗散量的多少与湍流速度、涡流速度、耗散体积成正相关；而与湍流尺度成负相关，当湍流尺度越小时，湍流强度越大，动能耗散越多。在进气道前添加一个耗散箱可以提前消耗进气动能，使得流入进气道的气体动能降低，减少了气体动能在灰斗和中箱体中的消耗，从而减少了二次扬尘的产生和提高了布袋使用寿命。

3) 改进后的脉冲式布袋除尘器，灰斗底部最大气流速度由原来19.2 m·s⁻¹降至9.6 m·s⁻¹，减少了二次扬尘的产生；中箱体底部最高气流速度由原来24.4 m·s⁻¹降至9.3 m·s⁻¹，减少了气流对布袋的冲刷，提高了布袋的使用寿命；全压相比原始布袋除尘器无明显上升；对于25、50和75 μm灰尘颗粒的沉降比例提高不太明显，但对于100、150、200、250和300 μm的灰尘颗粒沉降至灰斗里分别提高了11.4%、38.9%、59.6%、69.0%和71.6%。总体而言，提高了灰尘颗粒沉降效率，也提高了喷吹清灰下来的团聚颗粒的沉降效率，可有效减少布袋喷吹清灰频率，从而也减少了因喷吹次数过多造成的布袋损坏。