-
近年来,随着我国城市化进程发展和产业结构调整,许多企业关闭、停产、合并、转让,导致大量的工业有机污染场地被遗留在城区[1]。土壤修复技术众多,其中原位热修复技术具有环境干扰小、修复效果彻底以及可适用于低渗透性土质等优点,适合城市工业有机污染场地的修复,也被认为是未来土壤修复的主流方向[2-5]。原位热修复技术按加热方式不同,可分为原位蒸汽强化修复、原位电阻加热修复和原位热传导修复等多种形式[4]。
原位热传导修复技术因其具备修复周期短、可靠性高、适用性强,以及二次污染可控等优点,被证实是一种有效的原位污染土壤修复技术[6]。原位热传导修复技术利用电加热或燃气加热的方式对污染地块进行加热,土壤中水分及污染物受热蒸发、氧化或热解,大大提高了污染场地修复效率。原位热传导修复技术相比于其他原位修复技术,可将土壤加热至远超污染物沸点的温度[7]。据统计,目前该技术已有广泛的应用[8]。ZHAO等[9]认为,该技术降低了土壤挖掘和运输的成本、减少了对场地内建筑物的破坏和重建,且具有修复效率高、修复周期短等优点。
SUN等[10]和BASTON等[11]研究了原位热传导修复对地下传热过程及水文地质特性的影响,发现水文地质特性敏感的地下温度分布可决定污染物去除效率。迟克宇等[12]基于原位热传导修复技术开展了氯代烃类有机污染场地中试规模修复实验,探讨了不同加热井间距的升温速率及污染物去除率。ZHAO等[13]和HICKNELL等[14]通过实验对原位热传导修复技术油田场地适用性及地下温度反馈修复场地性能的准确性进行了研究,发现该技术在油田中具有实用性,局部尺度越过沸腾平台的温度升高不能代表NAPL-水共沸结束。XIE等[15]和XU等[16]通过数值模拟的方法对原位热传导修复技术共沸平台及供热控制策略进行了研究,以期降低能源消耗并指导工程实践。韩伟等[17]考虑了化学氧化、微生物降解及其他修复方式耦合原位热传导修复技术的现实意义,提出了工程方面降低能耗的具体举措。XIE等[18]模拟现场规模的原位热传导修复技术应用场景,探讨了土壤非均质性、NAPL构型及其质量采收率之间的关系。DAVIS等[19]和YU等[20]研究了原位热传导-气相抽提技术污染物去除路径及影响污染物迁移的关键因素。杨玉洁等[21]同样利用了原位热传导-气相抽提技术,研究了烃类污染土壤热脱附污染物去除效率的影响因素。综上所述,目前对原位热传导修复的研究主要集中在对修复过程的节能降耗、传热过程的影响因素、目标污染物的去除机理及去除效率方面,而对内部传热传质机理的认识尚不够清晰。
本研究基于土壤原位热传导修复单根加热棒小试实验及数值模拟,探究了原位热传导修复过程中土壤内传热传质机理,通过对比分析不同位置处的温升情况,以验证数值模型的准确性;并利用数值模型进一步分析了场地尺度下热源温度、初始含水率等因素对原位热修复效率的影响。本研究结果有助于预测修复周期、优化加热井排布设计,并有助于供热控制策略的调整,从而达到节约能源、实现可持续修复和降低修复成本的目的。
-
供试设备为原位热传导修复小试实验台,包括电加热棒(有效加热长度L=0.93 m)、电控箱、采集仪(安捷伦34972A)和圆桶(填充高度H=1.10 m,半径R=0.75 m)等。图1为该装置示意图。
供试土壤取自某修复场地,主要污染物为乙苯,土壤性质见表1。土壤采集后,去除土壤中大块沙砾,填充到圆桶内,填充高度为1.10 m,启动电加热棒,采集数据。
-
1) 控制方程。原位热传导修复实验涉及热湿耦合过程,本研究利用COMSOL传热模块和用户自定义的PDE模块,构建土壤热湿耦合传递模型,对模型作以下假设:1)忽略地表温度波动对土壤温度的影响,土壤初始温度均匀一致;2)由于污染物在土壤中占比小,原位热传导修复主要修复机制是污染物随着水蒸汽从土壤中挥发[22],故本研究忽略污染物的传热传质;3)将土壤视为均匀的、刚性的、各向同性的多孔介质[23-24];4)水的密度、导热性及比热容恒定不变;5)没有气体、固体和其他补给和化学反应的输入;6)土壤温度和含水率变化对土壤热物性的影响忽略不计。
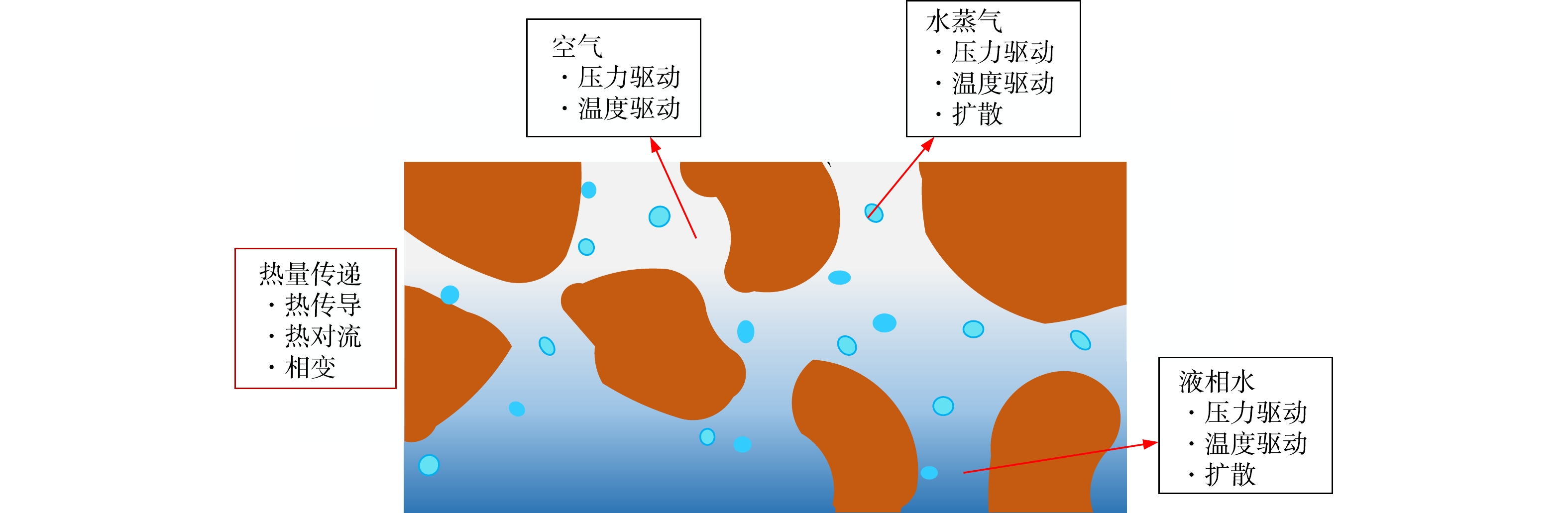
图2为土壤内热质迁移机制示意图,土壤一般被视为含湿多孔介质,热传导修复技术热源普遍是高温条件,液态水相变挥发,水蒸气充满土壤孔隙,孔隙中的气体受到温度和压力的驱动向外扩散,随着传热距离的增加,温度和压力驱动作用减弱、冷凝作用增强,最终温度、含水率达到动态平衡。由此可见,土壤内传热传质过程主要涉及土壤内热传导、热对流、相变以及水分的扩散,压力驱动等传热机理。
依据能量守恒方程,热传导控制方程利用局部容积平均法可表示为式(1)。
式中:
$\; {\rho }_{{\rm{eff}}} $ 为有效密度,kg·m−3;$ {c}_{{\rm{eff}}} $ 为有效比热容,J·(kg·K)−1;λ为导热系数,W·(m·K)−1;$ {\dot{E}\Delta H}_{{\rm{vap}}} $ 是热沉项,描述水蒸发引起的热量损失,W。土壤试样由固体颗粒、液体溶剂和填充在孔隙内的气体构成。在该计算模型中,$\; {\rho }_{{\rm{eff}}} $ 和$ {c}_{{\rm{eff}}} $ 根据式(2)和式(3)计算。式中:ρs为土壤密度,kg·m−3;Cs为土壤比热容,J·(kg·K)−1;θs为土壤孔隙率;ρL为液态水密度,kg·m−3;θL为液态水体积分数;CL为液态水比热容,J·(kg·K)−1;ρG为水蒸气密度,kg·m−3;θG为水蒸气体积分数;CG为水蒸气比热容,J·(kg·K)−1。
湿度控制方程见式(4)。
式中:DL是表观液体扩散系数;Ė是蒸发速率,kg·(m3·s)−1;Ė/ρL描述水蒸发引起的土壤质量损失。
蒸发速率与土壤中气体的饱和蒸汽压P*和平衡蒸汽压PG有关,平衡蒸汽压由ANTOINE方程所得,见式(5)~式(7)。
式中:α为比例常数;
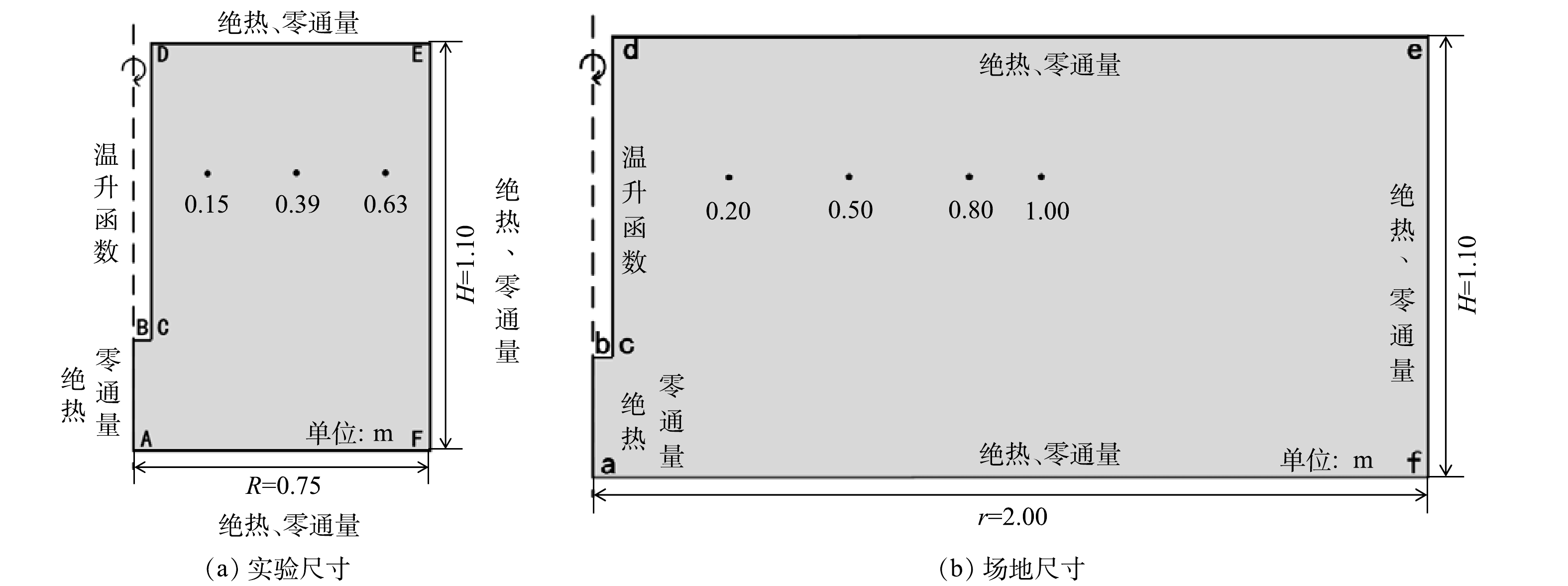
$ {\theta }_{{\rm{L}}}^{*} $ 为残余饱和度;kvap为蒸发速率常数,s−1;A、B、C取常数[25]。2) 物理模型和网格划分。为模拟工程应用环境下土壤内热量传递规律,将数值模拟分为2个部分。一是搭建实验尺寸几何模型(图3(a)),圆柱桶轴向切面为多边形A-B-C-D-E-F,区域内填充土壤。距A点轴向高0.70 m处,径向分布3个距A点长度为0.15、0.39和0.63 m的温度监测点。二是搭建场地尺寸几何模型(图3(b)),圆柱桶轴向切面为多边形a-b-c-d-e-f,区域内填充土壤。距a点轴向高0.70 m处,径向分布4个距a点长度为0.20、0.50、0.80和1.00 m的温度监测点。场地尺寸几何模型的建立,考虑了原位热传导修复实际应用场景各修复地块的相互独立、相互对称,且场地尺寸半径r=2.00 m为常见原位热传导修复加热井间距[26]。2部分几何模型的网格划分均采用三角单元网格,单元选择较细化。
3) 边界条件和参数设置。原位热传导修复数值模拟的初、边界条件为:1)流动边界条件,与外界接触的表面(D-E、E-F、F-A、d-e、e-f、f-a)均设置为零通量边界条件,这是因为已在方程中添加了质量汇项来描述水的蒸发;2)温度边界条件,边界C-D、c-d设置为热通量边界条件,内置经加热棒实验数据拟合得出的温升函数。边界D-E、E-F、F-A、d-e、e-f、f-a设置为绝热边界条件,初始时刻土壤温度为27 ℃。
4) 计算工况及参数。本研究以水为流体介质,研究原位热传导修复加热土壤耦合作用机理和其土壤基本参数变化对传热的影响效果,计算工况见表2,数值模拟相关参数具体见表3。
-
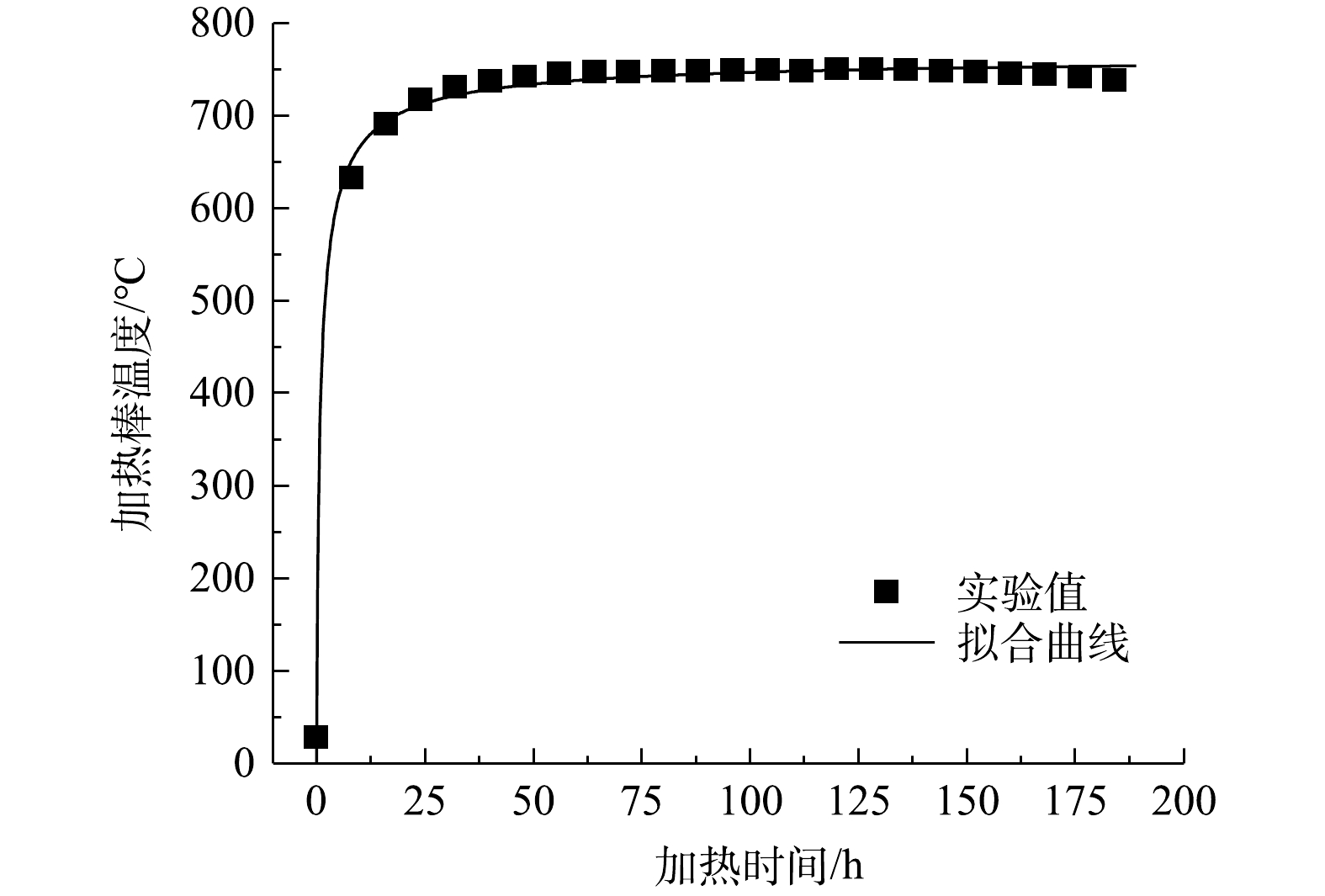
电加热棒实际温升响应曲线如图4所示。从图中可以看出,加热棒在较短时间内迅速升温到500 ℃,之后经历约30 h最终达到目标加热温度750 ℃。利用Hill函数对实验值进行拟合,得到电加热棒温升函数,具体表达式见式(8),R2为0.98。
式中:T为加热棒温度,℃;t为加热时间,h。该温升拟合函数与热通量边界条件结合,可优化数值模拟准确程度。
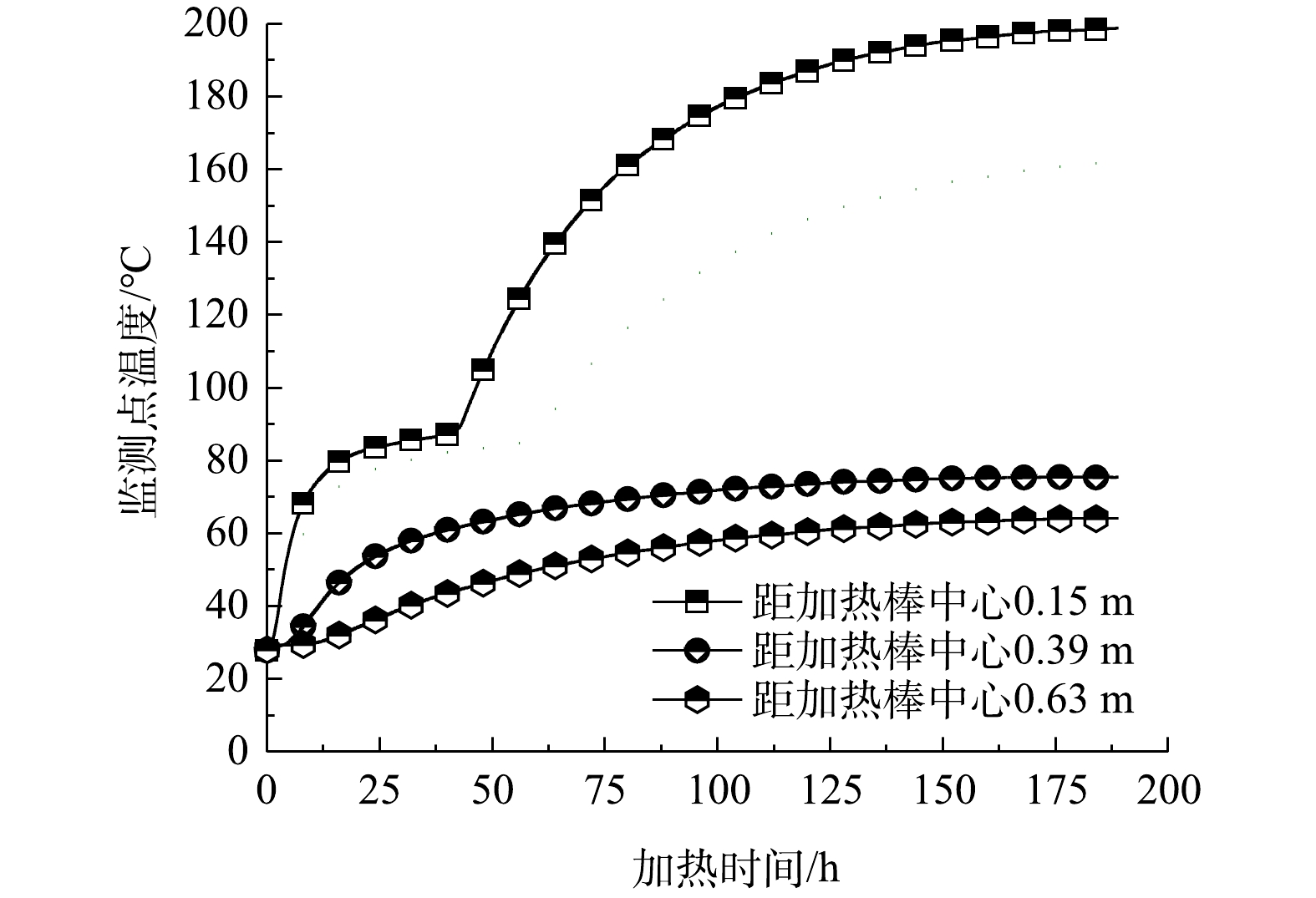
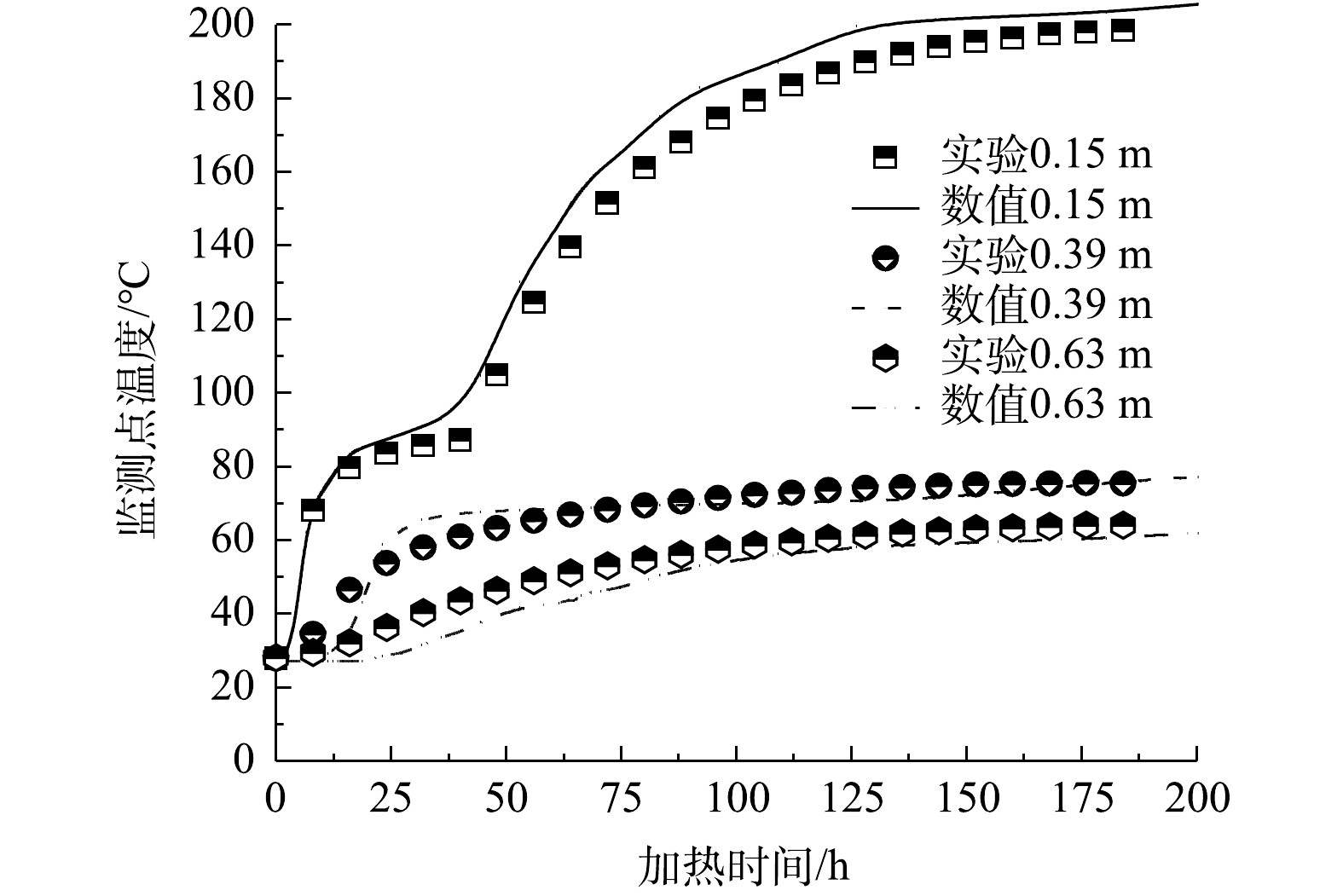
桶内的各测点温度与加热时间关系如图5所示。实验初始时,土壤温度为室内温度(约27 ℃),热源在短时间内迅速升温到500 ℃。根据傅里叶定律可知,热量将从较高温度流向较低温度,即从热源向壁面传递。在100 h时,3个监测点的温度分别为177、72和58 ℃。随着热量的扩散与损失,沿圆桶径向方向温升速率形成差异,离热源越近的监测点,温升越快。0.15 m监测点从土壤初始温度27 ℃升温到平台温度86 ℃用时40 h,升温速率为1.48 ℃·h−1,而0.63 m监测点从土27 ℃升温到64 ℃用时177 h,升温速率0.21 ℃·h−1。依据能量守恒定律可知,土壤中能量的输入和热量的损失达到平衡时,土壤温升平台即出现。0.15 m监测点在45 h时,由于土壤内液态水完全沸腾,故孔隙中不存在液态水,温度恢复持续上升。WANG等[27]和VINEGAR等[28]报道,土壤温升过程分为3个阶段,即加热阶段、沸腾阶段和过热阶段。此外,0.15 m位置处从沸腾温度86 ℃升温到197 ℃用时130 h,升温速率0.85 ℃·h−1,小于其加热阶段升温速率1.48 ℃·h−1。这是因为,加热阶段热量传递由水分迁移和固相传热耦合作用导致,这种热传导方式比单纯的固相传递更高效迅速。
-
为验证模型的可靠性,将不同距离处土壤温度的模拟值和实测值进行了对比,结果如图6所示。利用平均绝对误差MAE和平均相对误差MRE评价模拟值和实测值的吻合程度,其计算公式见式(9)和式(10)。
式中:n为实测数据个数;Mi、Si分别为第i个实测和模拟的数据。
经计算可得,实测值和模拟值最小平均绝对误差0.61,最小平均相对误差1.30%。较低的MAE和MRE值表明,实测数据与模拟数据之间的偏差较小,温度变化模拟结果合理可靠。
考虑整体温度变化,选取0.15 m处温度变化曲线,并选取3个特征值:沸腾阶段10 h、过热阶段100 h和终止190 h,做出三维温度等值面图,见图7。由该图可见,随着时间的增加,温度影响范围半径增大,并且温度以锥形向外扩散渐渐显著。在10 h,时锥形扩散并不明显,热量主要用于蒸发过量水分,由于水蒸气从顶部散失;在随后的100和190 h,底部变干明显,干导热系数低于湿导热系数,顶部传热速率大于底部传热速率,故出现锥形传热现象。
-
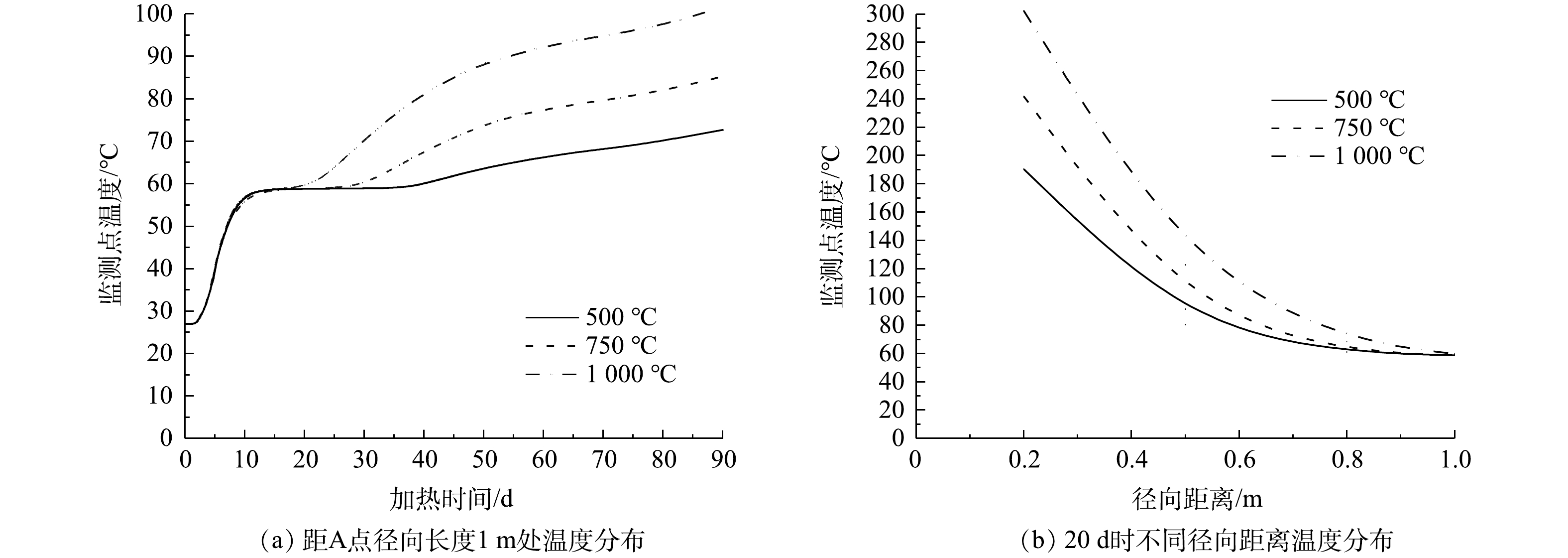
依据表2所列工况改变热源温度,添加500和1 000 ℃对照组。为了考察场地尺寸温度分布,建立了半径为2 m的几何模型[26]。依照热脱附工艺设计,将距离各加热井最远距离的位置定义为冷点[29],该数值模拟冷点位于径向距离1 m处。从图8(a)可以看出,热源温度可影响沸腾阶段持续时间和过热阶段升温速率。水的相变潜热值恒定,依据傅里叶定律,热源温度越大,则热流密度越大,沸腾阶段维持的时间亦越短。过热阶段液态水完全汽化,固相传热导热系数不变,热源温度越高,热通量越大,升温速率越大。3种不同热源温度在12 d时进入沸腾阶段,1 000 ℃热源在18 d时到达转折点进入过热阶段,750、500 ℃分别在24、34 d进入过热阶段。沸腾阶段维持时间分别为6、12和22 d。过热阶段,土壤从58 ℃升温到70 ℃所需时间分别为12、21和45 d,升温速率分别为1.00、0.57、0.27 ℃·d−1。3种温度在运行90 d后分别达到102、86和73 ℃,温度仍保持上升趋势,升温速率较低,短期内不会达到峰值。
此外,选取20 d作为时间节点,研究热湿耦合作用下不同径向距离温度分布,结果如图8(b)。可以看出随着热源温度增大,相同径向距离温度梯度越大,影响范围半径越大。土壤在0.2到0.5 m处的温差分别为179.53、150.44和109.81 ℃,温度梯度分别为598.43、501.47和366.03 ℃·m−1。1 000、750、500 ℃热源影响范围半径为1.0、0.8、0.5 m。由傅里叶定律可知,导热系数、水相变潜热值不变,温度梯度越大,热量损失变少,影响范围半径越大。图9为不同热源温度下温度等值面图,500 ℃影响范围半径最小,1 000 ℃影响范围半径最大。影响范围半径内1 000 ℃热源比750 ℃和500 ℃热源平均影响温度高。
-
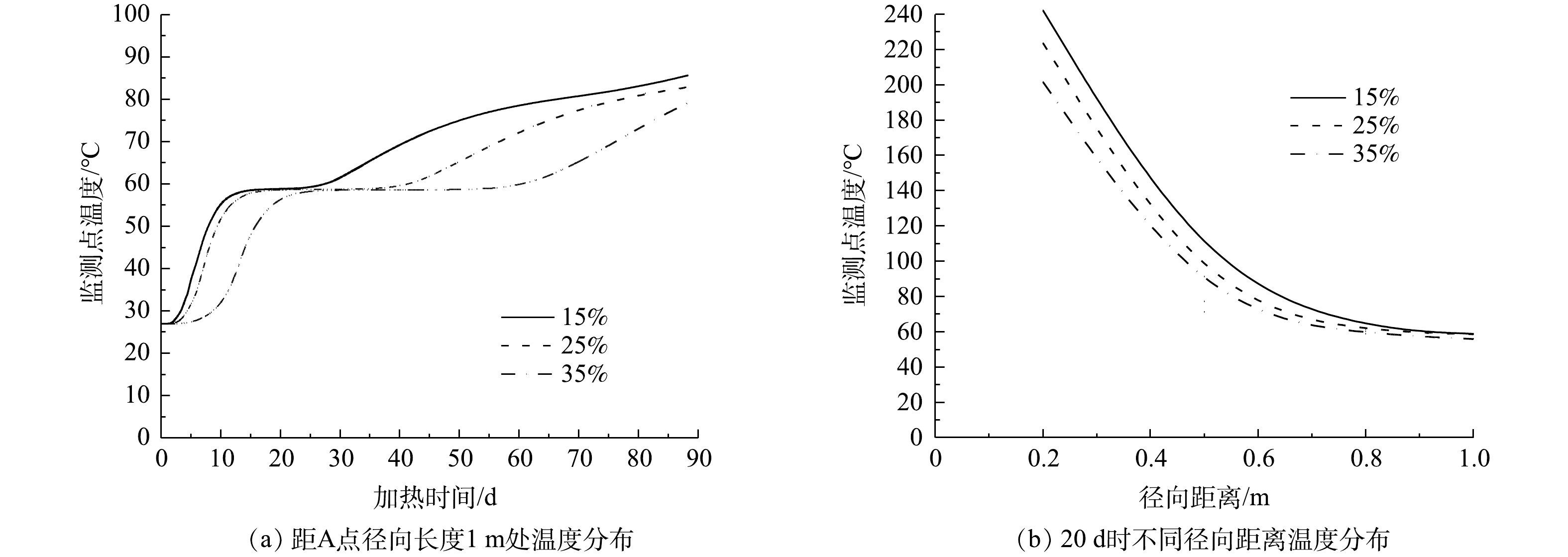
忽略非饱和土壤中水分含量的变化可能导致对热量传递的低估[30]。数值模拟A工况,发现土壤初始含水率对温度的影响可贯穿加热阶段和沸腾阶段,其中初始含水率越低,加热阶段温升速率越大,沸腾阶段维持时间越短,但沸腾阶段温度平台不发生变化。在加热阶段,热源温度(750 ℃)不变,则含水率越大,达到沸点温度过程中吸收的热量越多,升温速率越小。距A点径向长度1 m处,相同热源温度750 ℃影响下不同初始含水率温度分布如图10(a)所示,15%、25%和35%的土壤初始含水率从土壤初始温度27 ℃加热到沸腾温度58 ℃用时分别为12、15和23 d,升温速率分别为2.58、2.07和1.35 ℃ ·d−1。沸腾阶段,水相变潜热值不变,水分越多则相变潜热时间越长,3种初始含水率土壤分别维持13、26和34 d进入过热阶段。沸腾阶段平台温度与饱和蒸汽压和热源温度有关,热源温度一定,冷点处饱和蒸汽压不变,则平台温度不变。
不同初始含水率对热传导性能影响如图10(b)所示。初始含水率越大,温度梯度越低,则影响范围半径越小。图11为不同初始含水率下温度等值面图,可以看出,影响范围半径受初始含水率影响。15%、25%和35%的初始含水率土壤,在径向距离0.2 m处温度分别为242、223和201 ℃,在0.5 m处温度分别为91、77和71 ℃,温度梯度分别为503.33、486.67和433.33 ℃·m−1。不同初始含水率下温度影响半径为1 m。产生此现象原因有3点。1)导热系数和初始含水率呈正相关,初始含水率越大,温度梯度越低,导热系数越大。CAO等[31]阐述了“导热系数随含水率的增加而增大,但增幅随含水率的增加而减小”这一结论。2)影响范围半径是温度梯度和湿度梯度的竞争结果,初始含水率越大,湿度梯度越大,从而降低温度梯度影响,导致温度影响范围半径减小。3)初始含水率越大,水汽化潜热吸收热量越多,影响范围半径越小。
-
1)热湿耦合数值模型与小试实验平台的数据吻合较好,实测值和模拟值最小平均绝对误差0.61,最小平均相对误差1.30 %,本研究提出的热湿耦合数值模型具有可靠性。
2)对场地尺寸的数值模型进行研究,发现沸腾阶段持续时间与热源温度成反比,过热阶段升温速率与热源温度成正比,符合实际预期。模拟1 000 ℃热源温度在场地尺寸下运行90 d结果,在冷点处温度为100 ℃左右且温度仍在继续上升,耗能持续增加,故在原位热传导修复工程实践中应以去除目标为评价标准,而不是冷点温度。
3)场地尺寸原位热传导修复土壤初始含水率在15%~35%范围内,在相同热源温度影响下15%含水率土壤温度梯度大,导热系数高,故原位热传导修复优势场合为低含水率场地,高于15%初始含水率修复场地应进行适当排水,并应设置止水帷幕。
原位热传导修复过程中热量传递的数值模拟
Numerical simulation of heat transfer during in-situ thermal conduction remediation
-
摘要: 目前原位热传导修复技术存在热量传递机理不明、主要影响因子作用关系不清的问题,通过模拟室内土柱实验实现对土壤内部热湿耦合迁移机理的验证,并应用到室外场地尺寸,明确场地尺寸下热源温度、初始含水率对原位热传导修复的影响作用。建立了原位热传导修复耦合模型,利用小试实验对其进行了数值模拟验证,在场地尺寸下探究了热源温度、初始含水率对原位热修复的影响。结果表明,原位热传导修复耦合模型准确度较高,模拟结果与实验结果平均相对误差为1.30%。沸腾阶段持续时间与热源温度成反比,过热阶段升温速率与热源温度成正比,在工程实践中应以去除目标为评价标准而不是冷点温度。土壤初始含水率在15%~35%范围内,相同温度影响下含水率越低导热系数越高,原位热传导修复技术适用于低含水率场地,初始含水率高于15%,在进行修复之前应进行适当排水或设置止水帷幕。该研究结果可为原位热传导修复技术工程实践应用提供理论参考。Abstract: The current in-situ thermal conduction remediation technology has the problems of unclear heat transfer mechanism and unclear relationship between the main influencing factors. The verification of the coupled heat and moisture migration mechanism inside the soil is achieved by simulating indoor soil column experiments, and applied to the outdoor site size to clarify the effect of heat source temperature and initial moisture content on in-situ thermal conduction remediation under site size. An in-situ thermal conduction remediation coupling model was established, and a small-scale experiment was used to verify it by numerical simulation. The influence of the heat source temperature and initial moisture content on the in-situ thermal remediation was explored under the site size. The results showed that the in-situ thermal conduction remediation coupling model had high accuracy, and the average relative error between the simulation results and the experimental results was 1.30%. The duration of the boiling phase was inversely proportional to the temperature of the heat source, and the heating rate during the overheating phase was directly proportional to the temperature of the heat source. In engineering practice, the removal target should be the evaluation criterion instead of the cold spot temperature. The initial soil moisture content was within the range of 15%~35%. The lower the moisture content, the higher the thermal conductivity under the same temperature. The in-situ thermal conduction remediation technology was suitable for sites with low moisture content. If the initial moisture content was higher than 15%, proper drainage or water-stop curtains should be installed before restoration. The research results can provide a theoretical reference for the engineering practice application of in-situ heat conduction repair technology.
-
-
表 1 供试土壤性质
Table 1. Test soil properties
初始土壤
温度/℃土壤
含水率/%土壤干导热
系数/(W·(m·K)−1)土壤湿导热
系数/(W·(m·K)−1)土壤
孔隙率土壤比热容/
(J·(kg·K)−1)土壤密度/
(kg·m−3)乙苯质量分数/
( mg·kg−1)27 15 0.50 0.90 0.30 1 660 1 650 6.74 表 2 数值模拟计算工况
Table 2. Numerical simulation calculation conditions
工况编号 初始湿度/% 加热温度/℃ A-1 15 750 A-2 25 750 A-3 35 750 B-1 15 500 B-2 15 750 B-3 15 1 000 表 3 数值模拟参数
Table 3. Numerical simulation parameters
供试参数 设定值 供试参数 设定值 残余含水率 0.05 Antoine系数A 11.68 水比热容 4 182 J·(kg·K)−1 Antoine系数B 3 516.44 水蒸气比热容 1 800 J·(kg·K)−1 Antoine系数C −45.13 水蒸气密度 0.03 kg·m−3 蒸发速率常数kvap 9×10−6 s−1 -
[1] 杨洁, 黄沈发. 污染场地环境监管的上海路径[J]. 环境经济, 2016(17): 28-31. [2] HOU D, GUTHRIE P, RIGBY M. Assessing the trend in sustainable remediation: A questionnaire survey of remediation professionals in various countries[J]. Environmental Management, 2016, 184: 18-26. [3] SONG Y, HOU D, ZHANG J, et al. Environmental and socio-economic sustainability appraisal of contaminated land remediation strategies: A case study at a mega-site in China[J]. Sicence of the Total Environment, 2018, 610-611: 391-401. doi: 10.1016/j.scitotenv.2017.08.016 [4] DING D, SONG X, WEI C, et al. A review on the sustainability of thermal treatment for contaminated soils[J]. Environmental Pollution, 2019, 253: 449-463. doi: 10.1016/j.envpol.2019.06.118 [5] VIDONISH J E, ZYGOURAKIS K, MASIELLO C A, et al. Thermal treatment of hydrocarbon-impacted soils: A review of technology innovation for sustainable remediation[J]. Engineering, 2016, 2: 426-437. doi: 10.1016/J.ENG.2016.04.005 [6] ARESTA M, DIBENEDETTO A, FRAGALE C, et al. Thermal desorption of polychlorobiphenyls from contaminated soils and their hydrodechlorination using Pd- and Rh-supported catalysts[J]. Chemosphere, 2008, 70(6): 1052-1058. [7] 缪周伟, 吕树光, 邱兆富,等. 原位热处理技术修复重质非水相液体污染场地研究进展[J]. 环境污染与防治, 2012, 34(8): 63-68. doi: 10.3969/j.issn.1001-3865.2012.08.014 [8] 刘惠. 污染土壤热脱附技术的应用与发展趋势[J]. 环境与可持续发展, 2019, 44(4): 144-148. [9] ZHAO C, DONG Y, FENG Y, et al. Thermal desorption for remediation of contaminated soil: A review[J]. Chemosphere, 2019, 221: 841-855. doi: 10.1016/j.chemosphere.2019.01.079 [10] SUN H, QIN X, YANG X, et al. Study on the heat transfer in different aquifer media with different groundwater velocities during thermal conductive heating[J]. Environmental Science Pollution Research International, 2020, 27: 36316-36329. doi: 10.1007/s11356-020-09131-2 [11] BASTON D P, KUEPER B H. Thermal conductive heating in fractured bedrock: Screening calculations to assess the effect of groundwater influx[J]. Advances in Water Resources, 2009, 32: 231-238. doi: 10.1016/j.advwatres.2008.10.019 [12] 迟克宇, 李传维, 籍龙杰,等. 原位电热脱附技术在某有机污染场地修复中的应用效果[J]. 环境工程学报, 2019, 13(9): 2049-2059. doi: 10.12030/j.cjee.201905110 [13] ZHAO C, MUMFORD K G, KUEPER B H. Laboratory study of non-aqueous phase liquid and water co-boiling during thermal treatment[J]. Journal of Contaminant Hydrology, 2014, 164: 49-58. doi: 10.1016/j.jconhyd.2014.05.008 [14] HICKNELL B N, MUMFORD K G, KUEPER B H. Laboratory study of creosote removal from sand at elevated temperatures[J]. Journal of Contaminant Hydrology, 2018, 219: 40-49. doi: 10.1016/j.jconhyd.2018.10.006 [15] XIE Q, MUMFORD K G, KUEPER B H, et al. A numerical model for estimating the removal of volatile organic compounds in laboratory-scale treatability tests for thermal treatment of NAPL-impacted soils[J]. Journal of Contaminant Hydrology, 2019, 226: 103526. doi: 10.1016/j.jconhyd.2019.103526 [16] XU H J, LI Y Z, GAO L J, et al. Planned heating control strategy and thermodynamic modeling of a natural gas thermal desorption system for contaminated soil[J]. Energies, 2020, 13(3): 642. doi: 10.3390/en13030642 [17] 韩伟, 叶渊, 焦文涛,等. 污染场地修复中原位热脱附技术与其他相关技术耦合联用的意义、效果及展望[J]. 环境工程学报, 2019, 13(10): 2302-2310. doi: 10.12030/j.cjee.201906019 [18] XIE Q, MUMFORD K G, KUEPER B H. Modelling gas-phase recovery of volatile organic compounds during in situ thermal treatment[J]. Journal of Contaminant Hydrology, 2020, 234: 103698. doi: 10.1016/j.jconhyd.2020.103698 [19] DAVIS R J, LILJESTRAND H M, KATZ L E. Evidence for multiple removal pathways in low-temperature (200-400 °C) thermal treatment of pentachlorophenol-laden soils[J]. Journal of Hazardous Materials, 2020, 400: 122870. doi: 10.1016/j.jhazmat.2020.122870 [20] YU Y, LIU L, YANG C, et al. Removal kinetics of petroleum hydrocarbons from low-permeable soil by sand mixing and thermal enhancement of soil vapor extraction[J]. Chemosphere, 2019, 236: 124319. doi: 10.1016/j.chemosphere.2019.07.050 [21] 杨玉洁, 王春雨, 沙雪华,等. 烃类污染土壤热强化气相抽提技术的脱附动力学[J]. 环境工程学报, 2019, 13(10): 2328-2335. doi: 10.12030/j.cjee.201905119 [22] 孙袭明. 有机污染土壤热脱附技术的影响因素研究及模拟系统开发[D]. 天津: 天津大学, 2018. [23] 付建英, 徐化, 余权等. 原位热脱附修复污染土壤加热效果模拟和试验研究[J]. 能源工程, 2021(1): 70-73. [24] 於仲义, 胡平放, 袁旭东. 土壤源热泵地埋管换热器传热机制研究[J]. 煤气与热力, 2008, 28(12): 7-11. doi: 10.3969/j.issn.1000-4416.2008.12.003 [25] TOSUN I. Antoine Constants. In: The Thermodynamics of Phase and Reaction Equilibria[M]. Elsevier: the United Stastes, 2013: 667-669 [26] 熊樱, 蔡云, 王永敏,等. 原位燃气热脱附技术在有机污染土壤修复工程的应用[J]. 化工管理, 2020(31): 87-90. doi: 10.3969/j.issn.1008-4800.2020.31.043 [27] WANG W, LI C, LI Y Z, et al. Numerical analysis of heat transfer performance of in situ thermal remediation of large polluted soil areas[J]. Energies, 2019, 12(24): 4622. doi: 10.3390/en12244622 [28] VINEGAR H J, BONN M M. In situ thermal desorption (ISTD) of PCBs[C]//U.S. Department of Energy. Hazwaste World, Superfund XVIII. Washington,1997. [29] 王锦淮. 原位热脱附技术在某有机污染场地修复中试应用[J]. 化学世界, 2018, 59(3): 182-186. [30] LI C, CLEALL P J, MAO J, et al. Numerical simulation of ground source heat pump systems considering unsaturated soil properties and groundwater flow[J]. Applied Thermal Engineering, 2018, 139: 307-316. doi: 10.1016/j.applthermaleng.2018.04.142 [31] CAO D, SHI B, LOHEIDE S P, et al. Investigation of the influence of soil moisture on thermal response tests using active distributed temperature sensing (A-DTS) technology[J]. Energy Buildings, 2018, 173: 239-251. doi: 10.1016/j.enbuild.2018.01.022 -
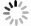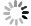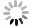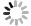


 下载:
下载: