-
随着工农业生产的快速发展,各种污染物质通过多种途径进入土壤环境并共存,造成了严重的土壤污染,其中多环芳烃是主要的污染物之一。近年来,多环芳烃在自然界中有不断累积的趋势,美国环境保护局已将其列为优先控制污染物,因此,开展对其污染土壤的修复治理研究具有重要意义。目前,关于土壤多环芳烃的修复技术主要有热力学、热解吸、焚烧、土地填埋、电动力学、化学淋洗、植物修复以及生物修复等[1]。其中,电动力学修复(electrokinetic repair, EKR)是通过施加一定的电压梯度,利用一系列电动运输现象(电渗透、电迁移、电泳)以及在土壤中发生的热和水力现象来将污染物迁移到受控提取点的土壤修复技术[2]。许多研究人员[3-5]对电场修复PAHs污染的土壤进行了初步的探究,也证明了其修复效果,关于EKR技术的修复PAHs迁移机制,却鲜少报道。
在过去的25年中,关于EKR的数学模型的研究一直在展开。KIM等[6]和WANG等[7]开发了关于化学平衡的一维数学模型,在此模型中考虑了孔隙水中的物质,电化学反应,扩散和电渗透输送以及离子的电迁移等因素。JACOBS等[8]通过添加偶联络合反应、吸附和沉淀/溶解过程来改进该模型,并将模型从一维域扩展到二维域。LÓPEZ-VIZCAÍNO等[9]提出了一个用于估计电动过程中pH分布的一维模型。MASI等[10]提出了一种基于Poisson-Nernst-Planck系统的运输模型,用于计算电渗平流和水化学平衡。PAZ-GARCIA等[11]提出了一种类似的去除镉的模型并由OTTOSEN等[12]推广,这种模型适用于受多种金属污染的土壤。RIBEIRO等[13]开发了一个适用于去除有机污染物阿特拉津的的模型实例,并开发了一个用于模拟在不饱和条件下土壤中离子的电动传输(假设在施加电梯度期间土壤中的电流类似于水流)的三维模型。
尽管关于EKR技术处理重金属和农药类污染物的数学模型已经有了大量的研究和比较成熟的应用,但关于多环芳烃类的数学模型却鲜少报道。因此,对基于实验和建模方法的EKR技术方案的实现是当务之急。本研究构建了电动体系中土壤菲的迁移模型,并探讨了相关因素对修复效果的影响以及土壤菲修复的主要机制,评估了新模型用于土壤中菲的去除可行性,为电动力学修复土壤有机污染物提供参考。
全文HTML
-
M4EKR模块(Multiphysics for EKR)是一种由客户端开发并在COMSOL Multiphysics中实现的多物理场模型。该模型用于模拟在受到外部电压梯度作用下,饱和土壤中溶质的反应性传输的过程。为了简化模型概念,假设温度条件为等温(298.15 K),气体压力(GP)保持不变并等于大气压。该模型并不代表真正被菲污染土壤的EKR过程。
水质平衡的计算方法如式(1)所示。
式中:Iw为水质通量,kg·(m2·s)−1;
$\nabla $ 为发散算子;mw为每单位总体积水的质量,kg·m−3。mw的计算方法见式(2)。式中:φ为土壤的孔隙率;Sr为土壤的饱和度;ρw为水的密度,kg·m−3;Iw为水的质量通量,为水力通量的总和,kg·(m2·s)−1。Iw的计算方法见式(3)。
式中:
$I_{\rm{w}}^{\rm{h}}$ 为用于达西定律和电渗透通量的计算;$I_{\rm{w}}^{{\rm{eo}}}$ 使用Helmholtz-Smoluchowski的半经验公式[14]估算;$q_{\rm{w}}^{\rm{h}}$ 为水力通量,m3·(m2·s)−1;$q_{\rm{w}}^{{\rm{eo}}}$ 为电渗通量,m3·(m2·V)−1;$\nabla $ 为梯度微分算子;g为重力加速度,m·s−2;z为纵坐标;PL为液体孔隙压力,Pa;E为电势,V;$K_{\rm{e}}^{\rm{h}}$ 为土壤有效水力渗透率,m·s−1;$K_{\rm{e}}^{{\rm{eo}}}$ 为电渗透率,m2·(s·V)−1;${K}_{{\rm{sat}}}^{\rm{h}}$ 为饱和水力渗透率,m·s−1;${K}_{{\rm{sat}}}^{{\rm{eo}}}$ 为饱和电渗透率,m2·(s·V)−1;αVG、nVG和mVG为VG拟合参数;s为基质吸力,定义为气体压力和液体压力的差值(PG−PL),假设PG恒为大气压。在M4EKR模块中模拟的一般地球化学系统中,考虑了在它们组合期间能够产生的N种化学物质的j种组分。为了确定系统的化学成分,应通过相应的质量平衡方程式了解每个组分的总量,根据式(9)进行计算。
式中:Ij为j组分的总摩尔通量,mol·(m2·s)−1;
$\nabla $ 为发散算子;mj为每单位总体积j组分的总摩尔质量,mol·m−3;Rj为组分j的生产或消耗率,mol·(m3·s)−1。由于可以通过满足电中性条件来确定系统组分的总质量,并且通过式(1)求解水质通量。因此,可以不必求解j的每一个的微分方程,只需对j的方程组进行求和。计算方法如式(10)所示。式中:
$I_j^{\rm{h}}$ 、$I_j^{{\rm{eo}}}$ 和$I_j^{{\rm{em}}}$ 分别为水力流、电渗流和电迁移产生的平流,$I_j^{{\rm{dif}}}$ 是Fickian扩散分散流。上述参数通过使用经典化学计量方法求解质量平衡和质量作用方程得到。这种方法已在已有研究[15, 8]中广泛描述。
总电荷在整个系统中具有电中性并假设不存在电荷累积容量,总电流密度可根据式(11)进行计算。
式中:
$\nabla $ 为发散算子;i为总电流密度,A·m−2,可根据欧姆定律[16]并使用文献中的方法[17-18]计算得出。在本研究中,放置电极的2个极室为阳极室和阴极室,用于冲洗土壤及除去收集的污染物。每个极室均可推导出如式(12)所示的微分方程,以实现每个组分的质量平衡。
式中:Rj*为组件的生产或消耗流量,mol·s−1;
$\dot M_j^{{\rm{in}},{\rm{*}}}$ 和${\rm{\dot M}}_j^{{\rm{out}},{\rm{*}}}$ 分别为组分j的流量输入和输出的总质量。来自系统的污染物最终通过阴极室流出,并且其朝向电渗水流动的方向移动。M4EKR模型完全在基于拉格朗日乘数的有限元方法的COMSOL Multiphysics的偏微分方程求解器中实现。COMSOL Multiphysics中包含的自动微分技术,提供了用于定义迭代矩阵的符号表达式,可以改善模型的收敛性,并且能在保持解决方案效率的同时提高问题的复杂性[19]。这种方法是地球化学规范中最常见的方法[20],其中一些方法,如PHREEQC程序[21],使用运算符-分裂程序[22]与其他模块耦合,以创建反应性传输代码。以这种方式,必须在每个时间步长和所有情况下以耦合方式解决大量状态变量。最后,为了更清楚地了解反应性传输过程,本研究使用二维域来模拟该过程。
-
实验试剂包括:无水乙醇(CH3CH2OH)、丙酮(CH3COCH3)、四氯化碳(CCl4)、氯化铵(NH4Cl)、重铬酸钾(K2Cr2O7)、乙酸铵(CH3COONH4)、无水硫酸钠(Na2SO4)均为分析纯;菲(C14H10)为优级纯;甲醇(CH3OH)为色谱级。
紫外-可见光分光光度计(UV-2550,日本岛津仪器有限责任公司);水浴恒温振荡器(SHY-2,金坛市大地自动化仪器厂);高速离心机(80-2型,江苏金坛新一佳仪器);索氏提取器(XMTD-4000,上海比朗仪器制造有限公司);旋转蒸发器(RE-2000A,上海亚荣生化仪器厂);氮吹仪(DN-24A,上海比朗仪器制造有限公司);马弗炉(KSW型,湖北英山县建力电炉制造有限公司);高效液相色谱仪(UltiMate 3000,美国戴安有限公司);pH计(ZD-18型,赛多利斯科学仪器有限公司);冷镜式露点仪(GDP-8000CM,武汉国电西高电气有限公司);直流稳压电源(FA-376 PROMAX,瑞轩电子科技(上海)有限公司);蠕动泵(BT100-2J,兰格恒流泵有限公司)。
采用重铬酸钾氧化法测定土壤的有机质含量;采用NH4Cl-C2H5OH法测定阳离子交换容量(CEC);土壤孔隙率根据容重和比重来确定;采用环刀法测定土壤容重;采用比重瓶法测定土壤比重;采用土壤pH计(ZD-18)测定土壤pH。电动力学实验前测得土壤阳离子交换量为12.1 cmol·kg−1,土壤含水率为30.0%,有机质为11.0 g·kg−1,土壤密度为1.640 kg·m−3,土壤pH为8.02,土壤孔隙率为0.380。采用索氏提取法提取土壤中的菲;采用用高效液相色谱仪测定菲的含量(C-18反向柱,250 mm×4.6 mm,5 μm),流动相为甲醇和水(90∶10),流速设置为1.0 mL·min−1,柱温为30 ℃,检测波长为254 nm;采用ASTM D-2435描述的一维固结方法估算水力渗透率
${K}_{{\rm{sat}}}^{\rm{h}}$ ;采用电渗透性细胞法[23]来估计${K}_{{\rm{sat}}}^{{\rm{eo}}}$ 。利用
$K_{{\rm{sat}}}^{\rm{h}}$ 和$K_{{\rm{sat}}}^{{\rm{eo}}}$ 进行拟合计算,得到2种渗透率的表达式,如式(13)和式(14)所示。采用冷镜露点式露点仪测定土壤的保留曲线,根据Van Genuchten模型,结合式(8)进行拟合,拟合方程如式(15)所示。根据拟合结果得到αVG、nVG和mVG的估值,其估值分别为14.7、1.38和0.206。边界参数
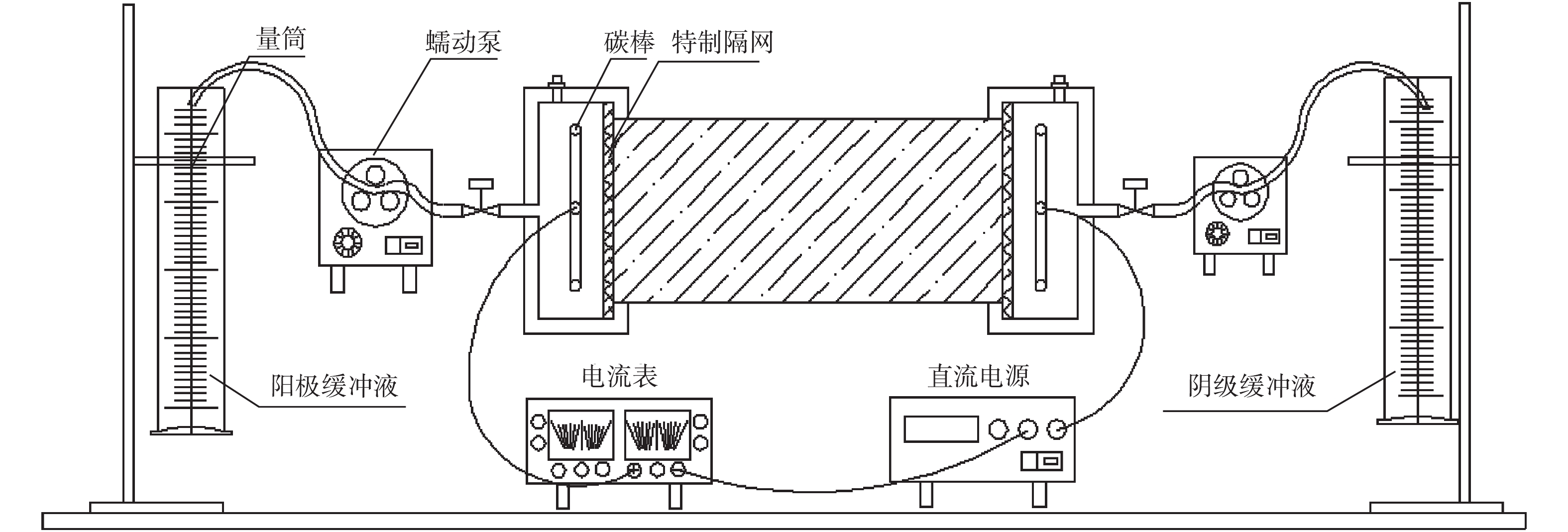
${\delta _T}$ 和Ґ分别取经验值[2]0.010 0和1.00。电动力学修复装置如图1所示。长方体有机玻璃反应器(长×宽×高为13.0 cm×5.00 cm×5.00 cm),阴阳极室(5.00 cm×5.00 cm×5.00 cm)以极室两端固定的石墨电极为反应器主体部分,用导线将阳极和阴极分别与电源正极和负极相连并串入万用表,有机玻璃圆柱与极室之间用滤纸和纱布隔开。阴阳极室分别加入0.104 mol·L−1的醋酸和醋酸钠作为电解缓冲液,并通过直流电源施加恒定电位梯度(0.500,1.00和2.00 V·cm−1)。
受试土壤为校园沙壤土,取自25.0 cm以上的表层土,拣去表面的枯枝和树叶,经风干磨细后过2.00 mm筛后储存待用。先将菲配制成浓度为100 mg·L−1的甲醇贮备液,于冰箱保存。根据文献中的方法[4],用电解质溶液配制菲溶液,并稀释成不同浓度的实验溶液。本研究选择含菲浓度为200 mg·kg−1的模拟污染土壤,实验前测定土壤中菲的初始含量、pH和含水率。装置运行结束后,测定不同区域菲的含量、土壤pH及含水量。
该建模初始条件和边界条件如下:孔隙率为0.380、修复区域长度为13.0 cm、压力为100 kPa、pH=8.02、阳极电压为13.0 V、阴极电压为0、水力梯度为0、菲的浓度为200 mg·kg−1。将水压常数PL0定义为整个区域中的初始水利条件,并且设定为含水率w和土壤孔隙率n的函数。在土壤和电极室界面重合的区域施加Dirichlet边界条件(第1类边界条件),PL=Patm=100 kPa。
1.1. 数学模型
1.2. 实验过程
-
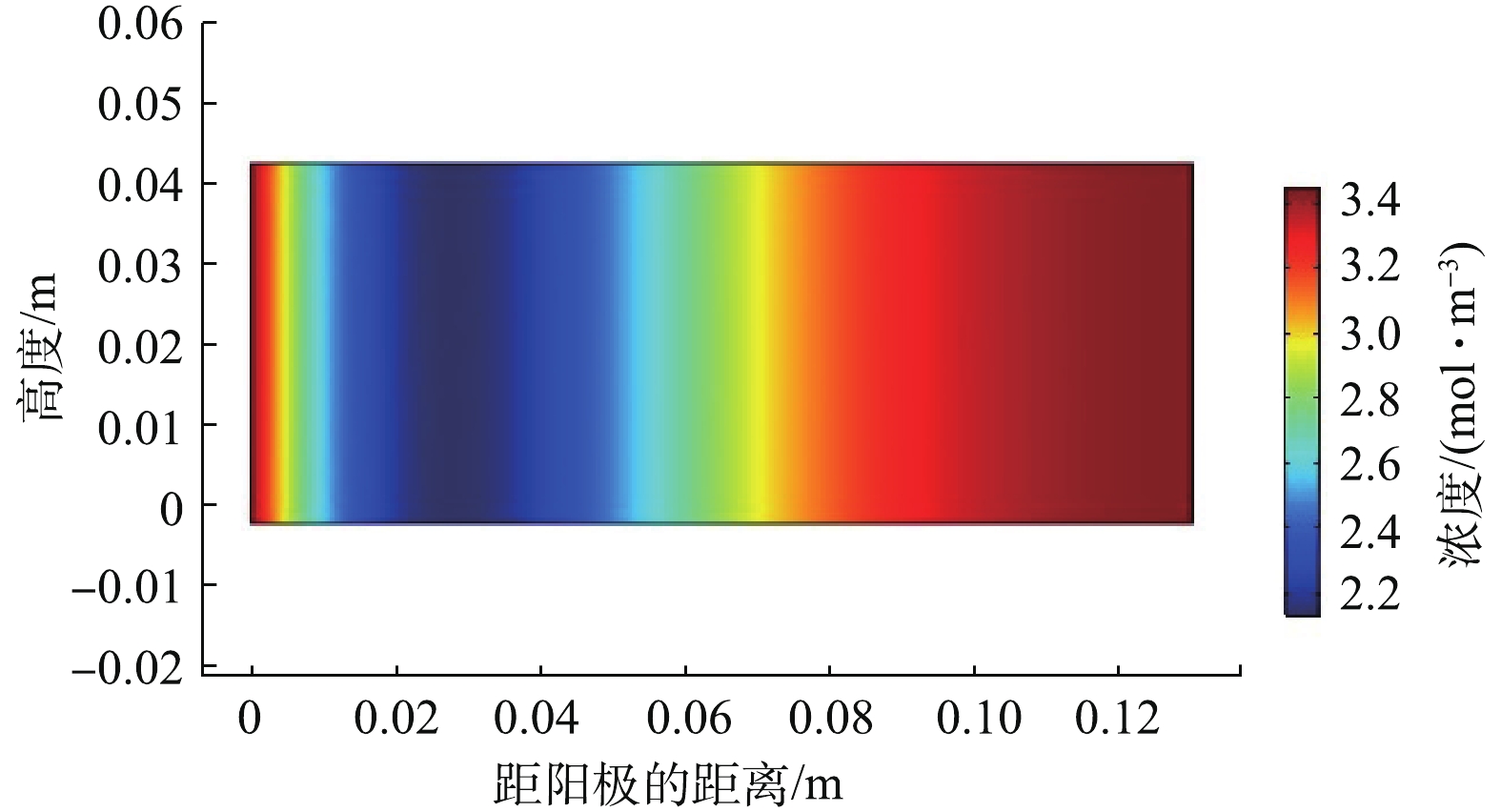
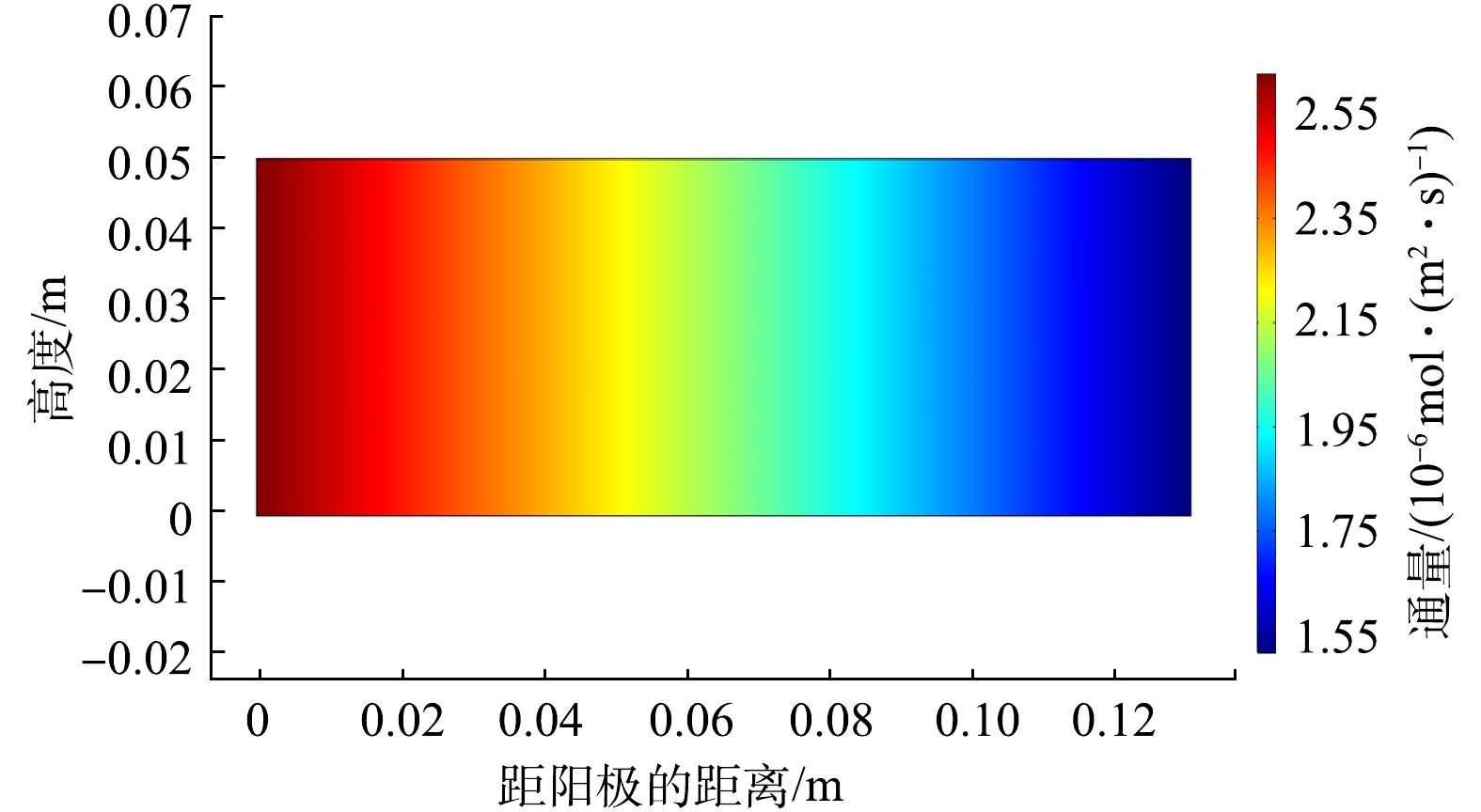
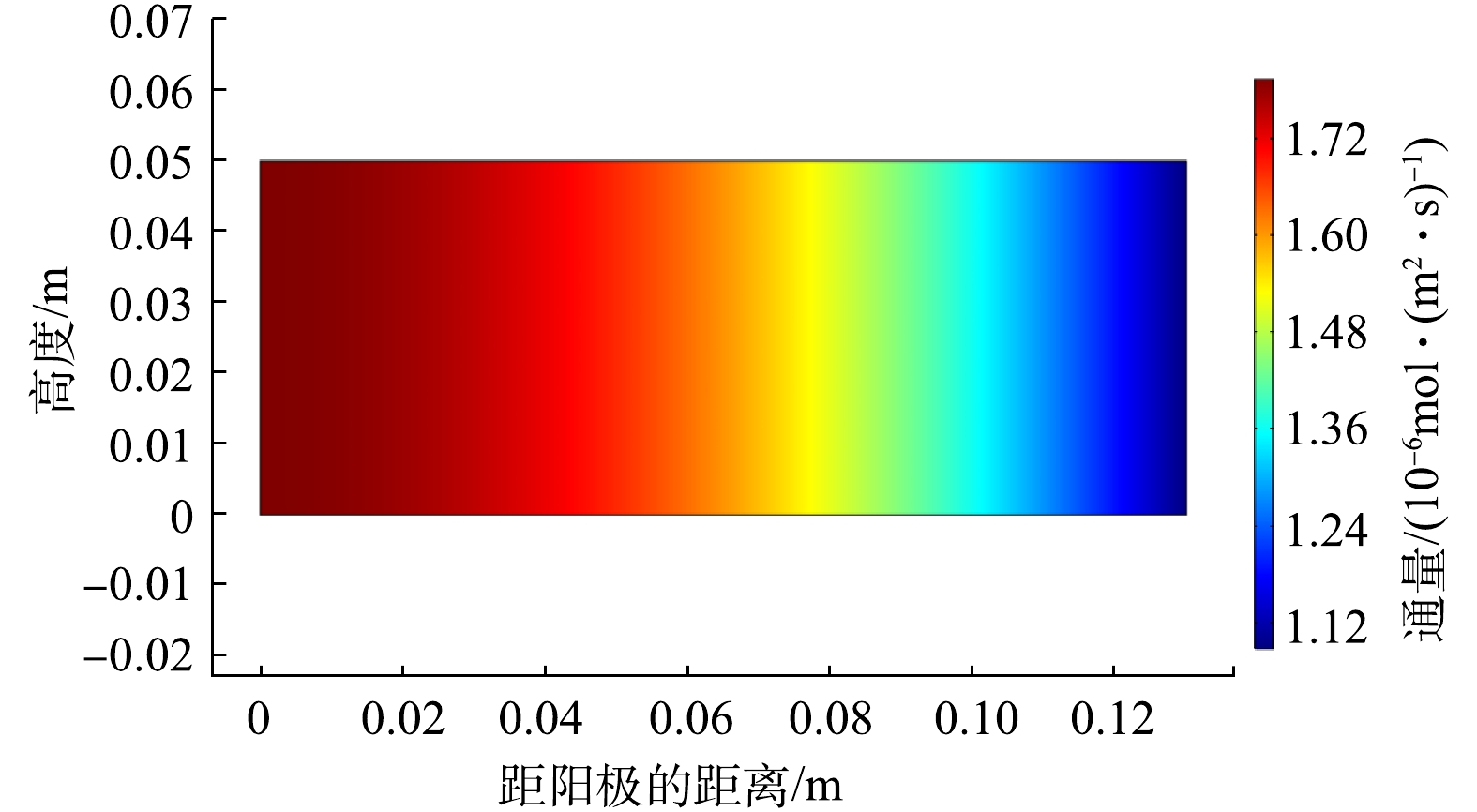
按照模型设定的条件,模型修复时间均为108 h。由图2可知,距离阴极越近,菲的浓度越大,菲的迁移方向主要是向阴极区迁移。电动修复结束后x轴方向总通量和电渗流通量的分布如图3和图4所示。从阳极到阴极,电渗流通量减小,说明电渗流在电动系统中的方向是从阳极指向阴极;而电渗流通量的大小也与总通量的大小比较接近,总通量和电渗流通量的最大值分别为2.63×10−6 mol·(m2·s)−1和1.81×10−6 mol·(m2·s)−1,说明电渗流通量在菲的迁移过程中起主导作用。这一模拟结果正好与PARK等[5]提到的溶解在表面活性剂APG(烷基糖苷)和Brij30(十二烷基聚氧乙烯醚)的高岭土中的菲通过电渗流作用被输送到阴极区域的实验结果相似。此外,这一结果还与PARK等[5]通过在电动土壤修复过程中在阳极引入阴离子表面活性剂(如Calfax 16L-35(十六烷基二苯醚二磺酸钠盐)等)与菲一起被迁移到阴极的迁移机理类似,说明菲的迁移主要以电渗流为主。
根据土壤的双电层理论,即土壤表面的负电荷与孔隙水中可交换阳离子能够形成扩散双电层,而双电层中可移动的阳离子数量比阴离子多,当施加电压时,阳离子对孔隙水的牵引力更甚,导致了土壤孔隙水朝着阴极区域运动,而菲具有非极性的特性,被包裹于孔隙水中,也随之向阴极区域迁移。此外,外加电场的非均匀性导致土壤菲分子被极化,如位移极化、变形极化、偶极趋向极化和驰豫极化。在某种程度上,极化后的菲分子等效于电偶极子,在其两端分别不断地积累正电荷和负电荷,于是导致两端合力不为0。然而土壤中各处的极化率不同,使得土壤菲开始趋向于或者远离场强最大的区域运动,即朝着两极运动。这表明菲的主要迁移方式为电渗流外和介电迁移。
-
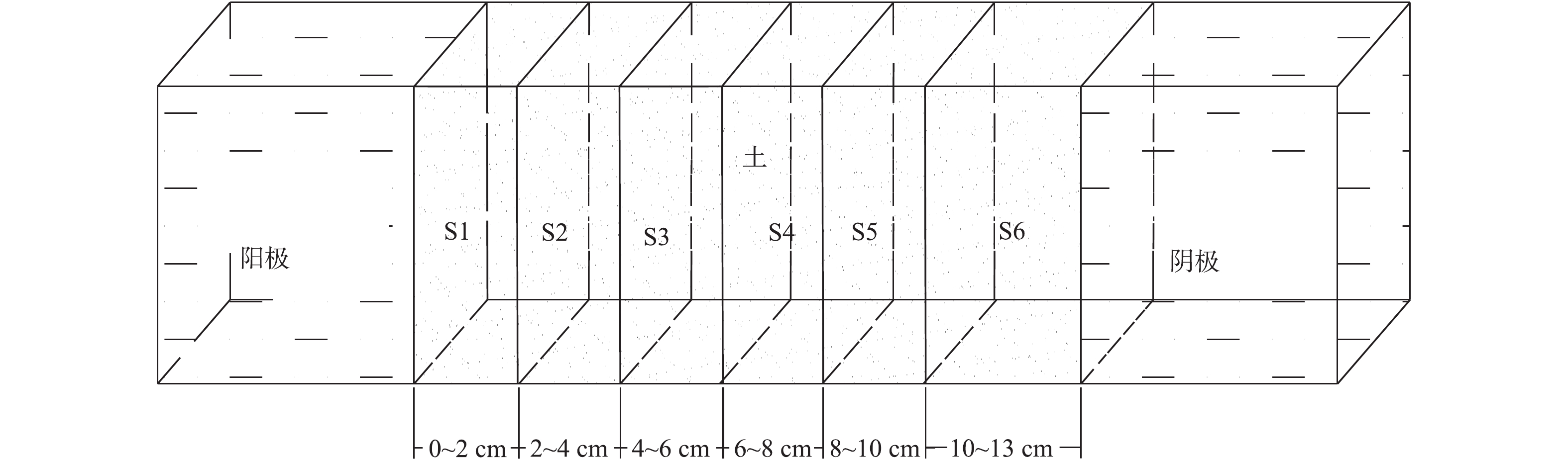
为验证模型的适用性,EK实验结束后,将土壤修复区域划分为S1~S6等6个区域。区域划分如图5所示,实验结束后各部分浓度与初始浓度见表1。
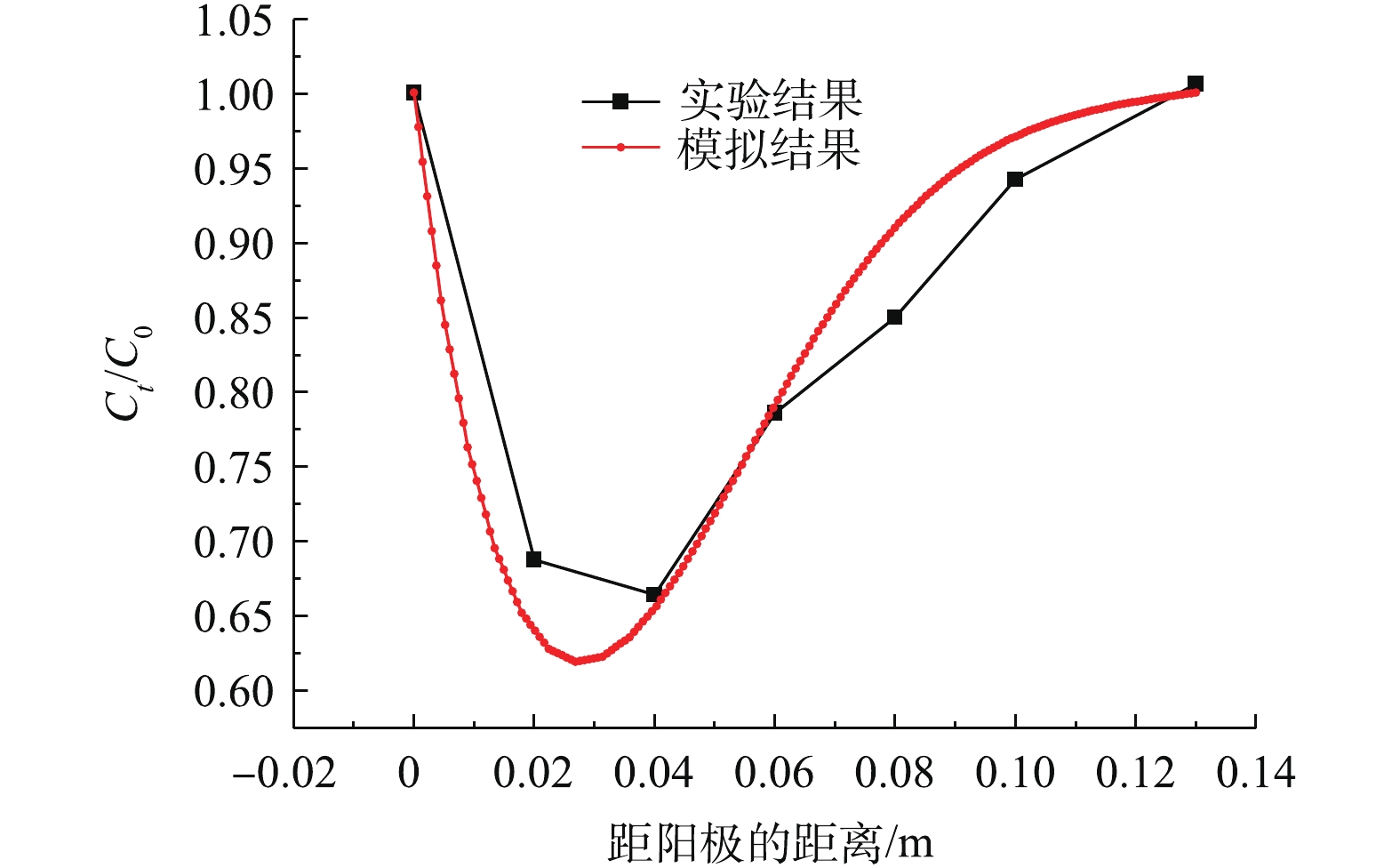
以距阳极的距离为横坐标,Ct/C0(C0为电动处理前菲的浓度,Ct为电动处理后菲的浓度)的比值为纵坐标,得出菲的分布曲线(图6)。可以看出,2条曲线均呈“碗状”分布,在两极区的菲的浓度均高于中间部分,说明菲的迁移方式是向两极区迁移的,这种迁移方式与马建伟等[4]的研究结果一致。而且在距离阳极3.00 cm的区域内,出现了Ct/C0的最小值(0.620),在该处的菲的迁移率达到了最大值(38.0%)。在电渗流的作用下,菲向着阴极方向迁移,由于介电迁移的影响使得菲在中间靠近阳极的部分向两边迁移,浓度达到最小值2.15 mol·m−3。相对模拟曲线而言,实验曲线位于模拟曲线的上方,其原因在于模型不能完全模拟菲在土壤中迁移的所有影响因素。在实际中,影响菲迁移的因素不只有电迁移、电渗流、对流、弥散,还有其他因素,如土壤黏度,pH、土壤的电导率等。
-
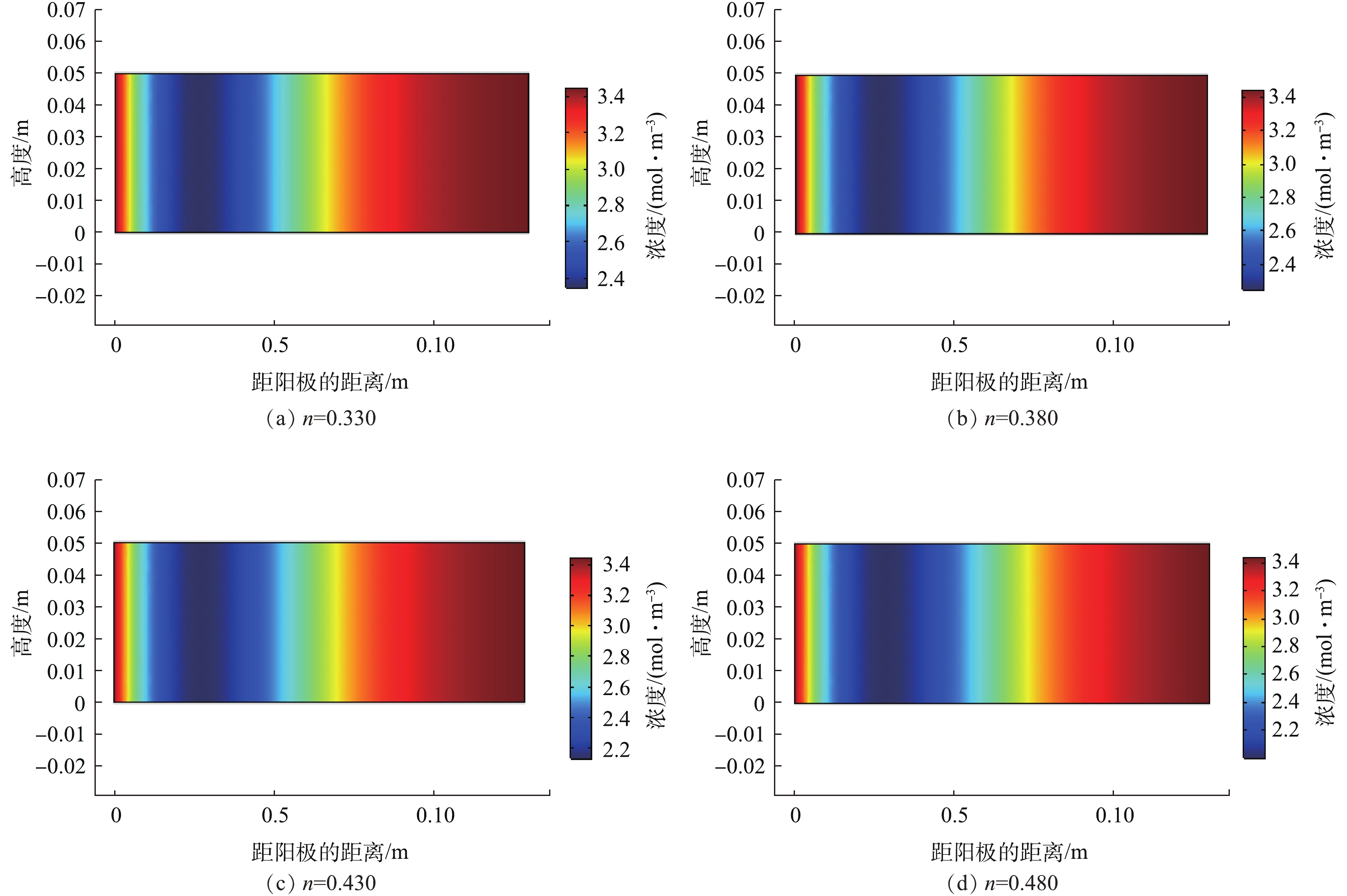
图7展示了土壤孔隙率为0.330、0.380、0.430和0.480时土壤菲浓度分布效果。当土壤孔隙率从0.330、0.380、0.430增加至0.480时,土壤菲浓度的最小值从2.35、2.25、2.14 mol·m−3增至2.01 mol·m−3,菲的迁移率从31.9%、34.8%、38.0%增至41.7%。由于土壤是由大大小小的孔隙、土壤颗粒等组成,土壤孔隙率常常可以反映土壤颗粒间间隙以及土壤的松紧程度,在一定程度上土壤孔隙率能够影响分子的扩散作用。在该模型中,土壤的黏性阻力和惯性阻力受到土壤孔隙率的影响较大。若土壤孔隙率较小,土壤颗粒之间较为密集,那么菲在土壤中扩散时所受到的黏性阻力和惯性阻力较大,其扩散动量也被削减,使得菲的分子速度减慢;相反,若土壤孔隙率较大,土壤颗粒之间较为疏松,那么土壤菲的扩散范围变大,即菲的扩散角度增大。此外,土壤孔隙主要由孔隙水和空气等组成,孔隙水的体积受土壤含水量影响较大,孔隙率可以表示为含水率的函数。若土壤含水率增大,土壤孔隙水的体积也增大,相应地电渗流作用也增强,从而导致菲的迁移效果也越好。
-
图8是电场强度为2.00 V·cm−1和0.500 V·cm−1时菲的浓度分布图。由图8和图2(电场强度为1.00 V·cm−1)可知,在3组电压条件下,菲的最大迁移率分别为44.4%、34. 8%和29.0%。由于菲具有非极性特性,使得菲迁移的驱动力主要来源于电渗流,而电渗流的驱动力主要源于电场力,因此,电场强度是影响电渗流通量大小的重要因素。随着电场强度的增大,土壤中的带电离子受到电场力增大,从而引起电渗流流速增大,电渗流通量也随之增大,即单位时间内通过截面的菲分子变多,菲的迁移速率加快,使得两极区域菲的浓度均变大,最终导致土壤菲的电动修复效果较好。
2.1. 模拟结果
2.2. 模型验证
2.3. 孔隙率对菲迁移的影响
2.4. 电场强度对菲迁移的影响
-
1)通过土壤菲修复的电动力学实验确定模型的边界条件和初始条件,并结合COMSOL Mutiphysics 5.3软件,构建了电动体系中土壤菲的多物理场仿真迁移模型,证明了该模型用于评估土壤菲的去除是可行的。
2)通过该模型探索土壤孔隙率和电压条件对土壤菲迁移效果的影响,可以看出:当孔隙率从0.330、0.380、0.430增大至0.480时,土壤菲的迁移率从31.9%增至41.7%,说明孔隙率对迁移效果影响较大;当电压梯度从0.5 V·cm−1增至2 V·cm−1时,菲的迁移率从28.99%增至44.35%,说明电压对菲的迁移效果影响较大。
3)通过探索土壤孔隙率和电压条件对土壤菲的迁移机制,结果表明:随着土壤孔隙率的增大,土壤菲的分子扩散通量增加,传质效率越高,说明土壤孔隙率的增大在一定程度上促进了土壤菲的迁移;外加电压的施加导致了修复区域电流的增大,电渗流也随之增大,从而加快了土壤菲的迁移。


 下载:
下载: