-
抽出处理技术是有效的地下水修复技术之一，该技术具有快速阻断污染物迁移和有效去除地下水中污染物的特点，在国内外应用较为广泛[1-3]。影响地下水抽出效率的因素主要有抽水流量、抽水方式、抽水井数量及其布设位置[2, 4]。确定抽水井位置及数量，需要掌握污染羽的分布、场地水文地质条件及特定抽水流量下单井捕获半径及驻点值[5-6]。JAVANDEL等[7]用复变函数理论定量研究了均匀流态下承压完整井形成的截获带，以解析解形式表示了单井捕获半径及驻点。从地下水势叠加原理出发，GRUBB[8]提出了潜水和承压水含水层中抽水井形成的稳定态捕获半径及驻点的解析表达式，但该公式未考虑抽水引起的降落漏斗、渗漏及入渗补给等因素对表达式的影响，误差较大，较少应用。关于补给条件下捕获半径及驻点的研究成果，迄今鲜有文献报道。对各向异性含水层中存在补给的捕获半径及驻点定量研究，各国学者趋向于采用数值模拟方法[9-10]。截至目前，定量获取单井及多井捕获半径、驻点的方法主要有3种，分别为抽水实验实测法、解析解公式计算法、数值模拟法；3种方法各有优点，又各自存在局限性。解析解计算公式适用于均质、等厚的承压含水层或水位降深相对总的饱和带厚度很小的潜水含水层[7, 11-12]；解析解公式计算法简便易行，但针对潜水抽水井捕获半径计算尚未有合适的解析解公式。刘明柱等[13]运用数值模拟方法来获取抽水井捕获半径及驻点；数值模拟法更适用于水文地质复杂条件情况，其精度在于对场地水文地质条件掌握程度[14-17]。抽水实验实测法适用条件广、精度高，但须布设较多监测井，成本较高。本研究分别采用上述3种方法对潜水、承压水不同类型场地抽水井的捕获半径及驻点值进行了计算，以确定不同条件下捕获半径及驻点获取的最优方法，为不同类型场地抽水井捕获半径及驻点获取方法提供参考。
-
1)承压水类型场地概况。研究区位于湖南某铁合金厂，厂区面积为55×104 m2。岩性(厚度)由地表向下依次为杂填土(5 m)、粉质黏土(3 m)、细砂圆砾(5 m)、泥质粉砂岩(4 m)。地下水类型为承压水，含水层近于等厚，约为5 m。地下水赋存于细砂及圆砾层，水力坡度约为0.006，地下水埋深约为3 m，地下水流向为自西北向东南，其补给来源主要为上层滞水的越流补给及区域地下径流侧向补给，排泄方式主要为人工排泄及向东侧河流分散排泄。
2)潜水类型场地概况。研究区位于湖南某铬盐厂，厂区面积为14×104 m2。岩性(厚度)由地表向下依次为杂填土(厚度8 m)、细砂圆砾(厚度6 m)、强风化板岩(厚度8 m)。研究区地下水赋存于细砂、圆砾层及强风化板岩层，地下水类型为潜水。本次主要针对第四系松散岩类孔隙潜水含水层开展研究。第四系松散岩类孔隙含水岩组孔隙度为0.25，水力坡度约为0.002。地下水埋深约为8 m，含水层厚度约为6 m，地下水流向为自西北向东南，主要接受大气降雨及区域地下径流侧向补给，排泄方式主要为人工排泄及向东侧河流分散排泄。
-
在水力梯度为i的均匀流含水层中，若以流量Q抽取地下水，含水层中将出现一个地下水的分水线。将地下水分为2个区域，分水线以外的地下水仍将流向下游区域，而分水线以内的地下水则会被抽水井抽出，不再流向下游，称此区域为该抽水井的捕获区域(图1)。在抽水井所在的轴线上，地下水的分水线与轴线相交于点x=−xL，在该点上游的地下水将被抽水井抽出，而该点下游的地下水将流向下游区域。作为临界点，点x=−xL处的地下水流速为零，一般称该点为驻点。科学合理地布设抽水井是应用抽出处理技术的关键，获取单井捕获半径、驻点值可为抽出处理方案中抽出井流量及位置布设提供设计依据。
1)抽水实验实测法。抽水实验实测法是一种利用抽水井抽水的同时观测其周边监测井水位变化，通过实测水位变化来确定抽水井捕获半径及驻点的方法。该方法实测出的抽水井捕获半径与驻点值准确度较高，其精度在于监测井的布设密度，密度越大，精度越高；但该方法操作复杂，实验周期长、费用较高。
2)解析解公式计算法。本研究所用解析解公式为捕获半径及驻点计算的理论公式[7]。假设单个抽水井抽水时位置在原点，则捕获带与非捕获带分水岭的方程[5]见式(1)和式(2)。
式中：yL为捕获半径，m；xL为驻点，m；Q为抽水量，m3·d−1；B为含水层厚度，m；K为渗透系数，m·d−1。
式(1)和式(2)的应用假设条件为含水层承压等厚，其厚度为B；对于潜水，如果水位降深变化相对总的饱和带厚度很小，可利用该公式进行近似计算。如果水位降深变化相对总的饱和带厚度很大，该公式则不适用。
3)数值模拟法。数值模拟法是运用数值模拟软件概化水文地质条件，建立水流模型，进而计算抽水井捕获半径及驻点的方法。该方法操作简单，所需费用较小，计算捕获半径及驻点值的准确程度在于对场地水文地质条件的掌握程度。
-
1)承压水类型场地参数计算。通过3次不同降深的单孔稳定流抽水实验[18-20]，利用裘布依公式计算得承压含水层的平均渗透系数为6.81 m·d−1。
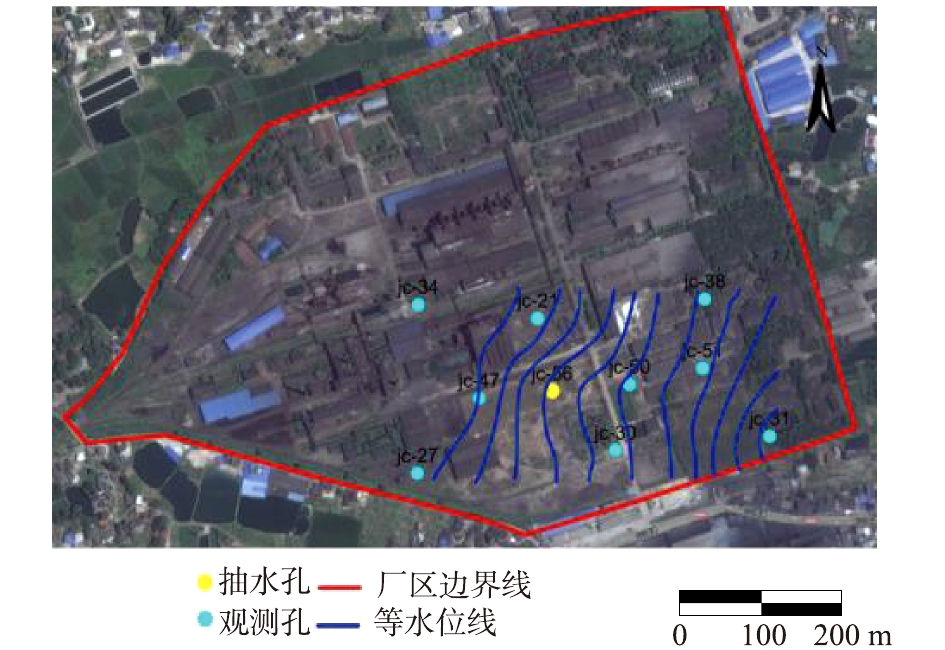
天然条件下区域地下水整体流向自西北向东南。以56号井为抽水井，通过监测抽水前及水位降深稳定后抽水井附近的9个观测孔水位，刻画承压含水层流场的变化(见图2和图3)。结果表明：单井抽水流量为120 m3·d−1时，驻点位于50号井和51号井之间，驻点距离抽水井约95 m，捕获半径约为290 m。
2)潜水类型场地参数计算。为得到场地孔隙含水层的渗透系数，通过3次不同降深的单孔稳定流抽水实验，利用裘布依公式计算得出潜水含水层的渗透系数为18.78 m·d−1。
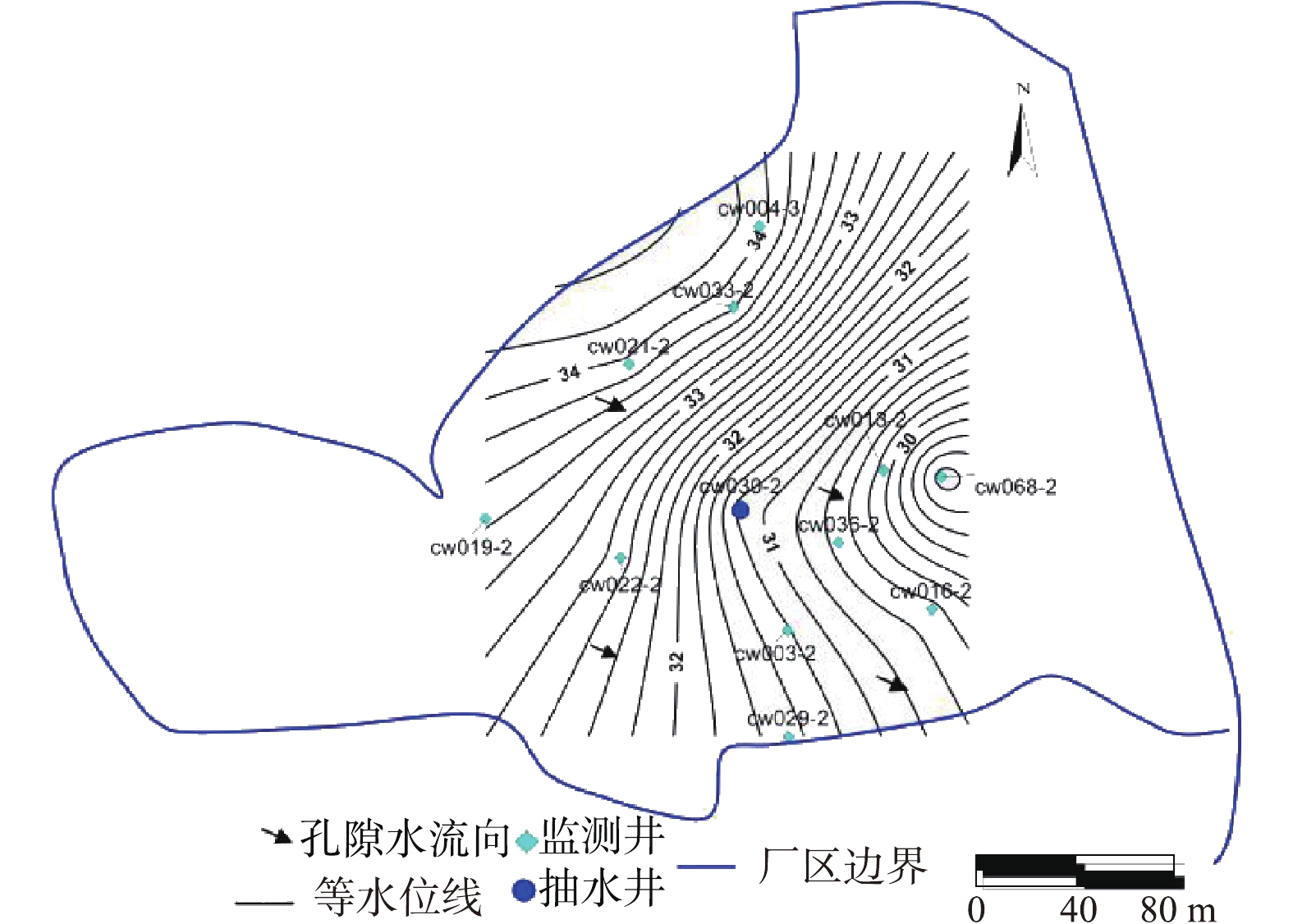
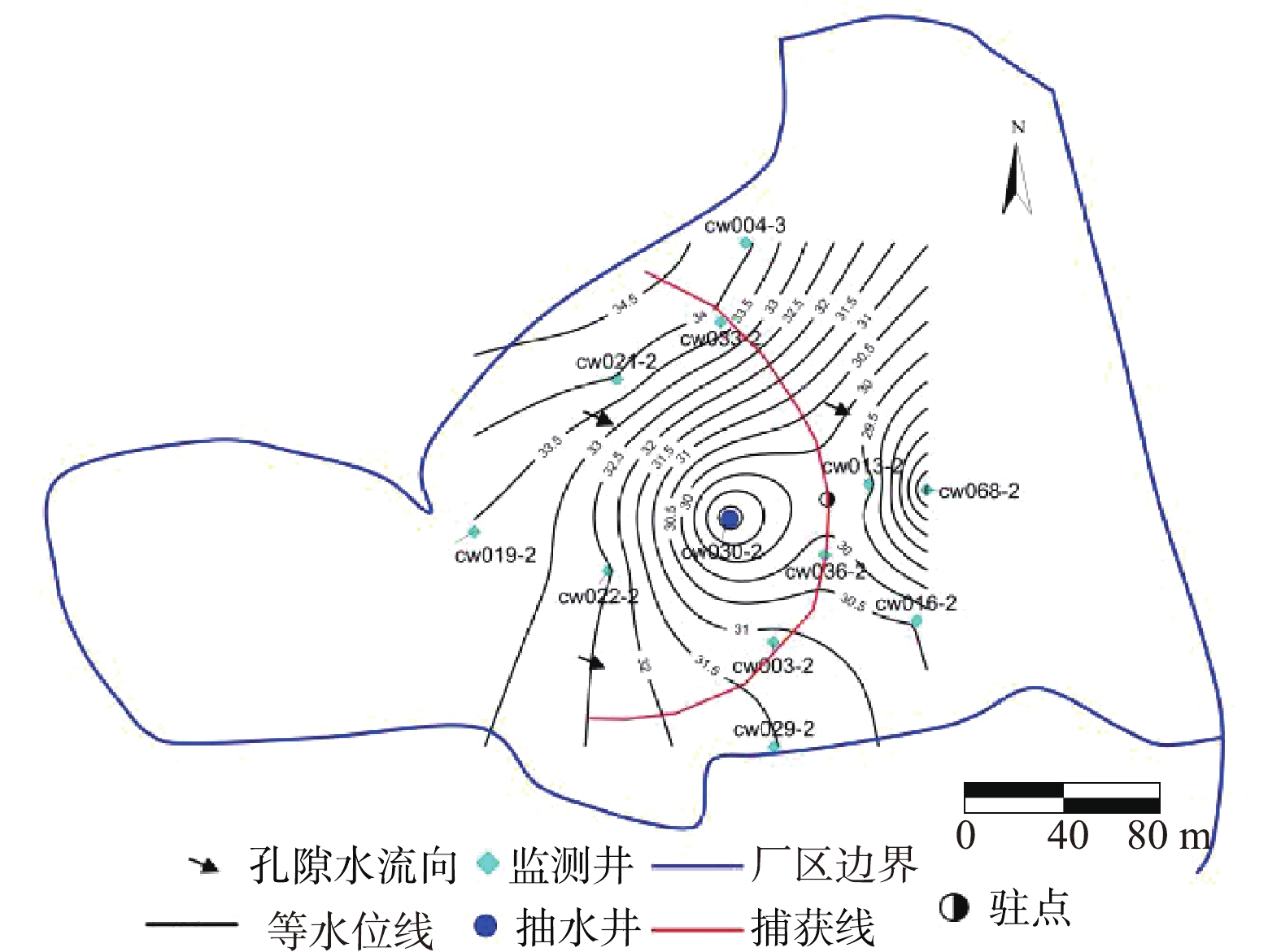
天然条件下区域地下水整体流向自西北向东南。以30号井为抽水井，通过监测抽水前及水位降深稳定后抽水井附近的11个观测孔水位，刻画潜水含水层流场的变化(见图4和图5)。结果表明：单井抽水流量为60 m3·d−1时，驻点位于30号井和13号井之间，驻点距离抽水井约55 m，捕获半径约为88 m。
-
1)承压水类型场地参数计算。单井抽水流量为120 m3·d−1时，水位稳定降深为4.25 m，水位未下降至承压含水层隔水顶板以下，满足式(1)和式(2)的假设条件，利用公式计算得出单井抽出水量为120 m3·d−1时，单井捕获带半径为293.7 m，驻点为93.5 m。
2)潜水类型场地参数计算。单井抽水流量为60 m3·d−1时，稳定水位降深为2.83 m，水位降深相对于含水层厚度不可忽略，利用式(1)和式(2)计算，得研究区单井捕获带半径为33.28 m，驻点为10.60 m。
-
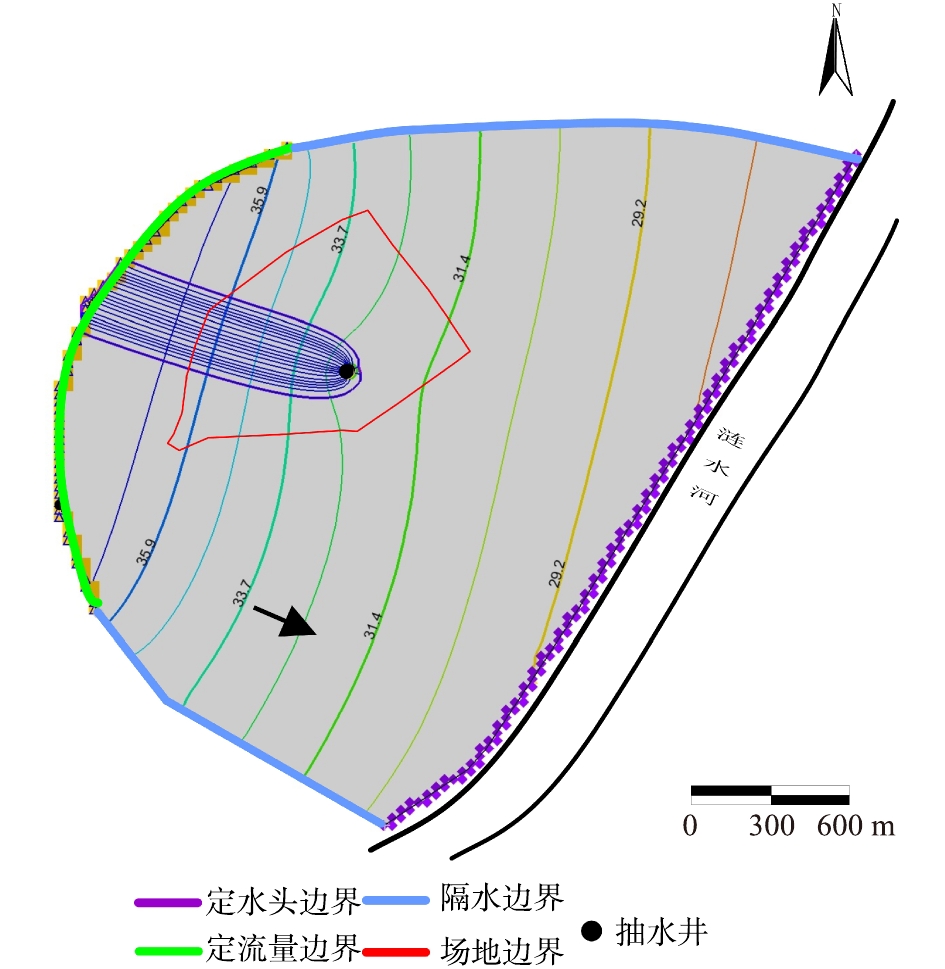
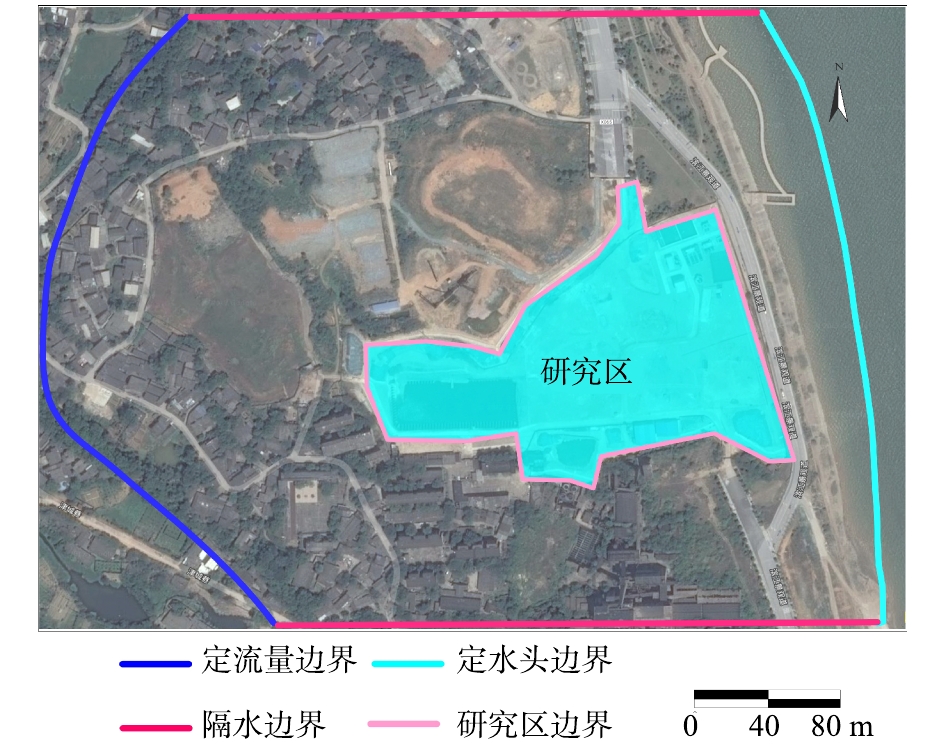
1)承压水类型场地参数计算。研究区承压含水层介质类型单一，可概化为均质各向同性含水层。研究区东部临河，为主要排泄边界，将其设为定水头边界；西部为地下水补给边界，将其概化为定流量边界；北部和南部垂直于地下水流方向设为零流量边界(图6)。承压含水层顶部为粉质黏土，底部为泥质粉砂岩，将其概化为隔水层。
在建立水文地质概念模型的基础上，利用GMS建立地下水流数值模型，网格剖分采用有限差分的离散方法，模型共1层网格，模拟承压含水层，将该区域剖分为100×100的网格。根据研究区场地调查结果确定场地渗透系数为6.81 m·d−1，经模拟识别和模型验证给水度为0.1，孔隙度为0.25，弥散系数为10 m2·d−1。在建立水流模型的基础上，布设抽水井56号孔，抽水流量为120 m3·d−1，从单井捕获半径粒子追踪图(图6)可得，单井捕获半径为285 m，驻点距离抽水井为98 m。
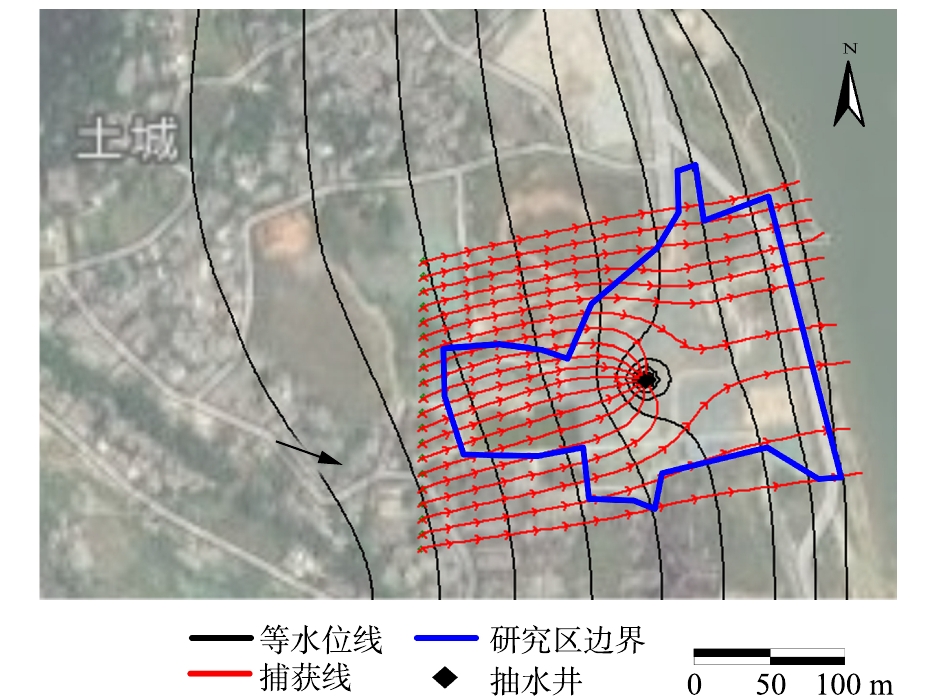
2)潜水类型场地参数计算。研究区为潜水含水层，岩性单一，概化为均质各向同性含水层，地下水概化为二维稳定流，边界条件概化：研究区东部临江，为主要排泄边界，将东部边界设为定水头边界；西部有地下水径流存在，为地下水补给边界，将其概化为定流量边界；北部和南部垂直于地下水流方向概化为隔水边界(图7)。
在建立水文地质概念模型的基础上，利用GMS建立地下水流数值模型，网格剖分采用有限差分的离散方法，模型共1层网格，模拟孔隙潜水含水层，将该区域剖分为80×80的网格。
根据研究区调查结果确定场地渗透系数为18.78 m·d−1，模型识别与模型验证后确定含水层给水度为0.07，孔隙度为0.25，弥散系数为8 m2·d−1。在建立水流模型的基础上，布设抽水井，抽水流量为60 m3·d−1，从单井捕获半径粒子追踪图(图8)可得，单井捕获半径为84 m，驻点距离抽水井约50 m。
-
针对以上2类场地，以抽水实验实测值为准，分别求取了解析解公式计算值及数值模拟值相对于抽水实验实测值的误差。不同方法获取抽水井捕获半径及驻点值误差对比分析结果见表1。从表1中可以看出，对于承压水类型场地，利用解析解公式和数值模拟所得值相对于抽水实验实测值误差较小，分别为1.6%和3.2%，均在5.0%以内。这说明3种方法获取捕获半径、驻点均较为可靠，但实测法成本较高，数值模拟法对水文地质条件掌握程度的要求较高，解析法相对效率高、成本低。因此，对于水文地质条件相对简单的承压水类型场地，建议采用解析法获取不同流量下的捕获半径及驻点值更合理。
对于水位降深变化相对于含水层厚度不可忽略的潜水类型场地，利用解析解公式计算值相对于抽水实验实测值偏离较大，高达80.7%，利用数值模拟方法的计算值相对于抽水实验实测值偏离较小，为9.1%。由此可见，当场地条件不符合解析解计算公式假设条件时，计算得到的捕获半径及驻点值与实际情况偏离较大，数值不具有参考意义。因此，在计算水位降深变化相对于含水层厚度不可忽略的潜水类型场地捕获半径和驻点时，须对场地开展详细的水文地质调查，再采用数值模拟法获取抽水捕获半径和驻点值更适宜，结果见表1。
-
1)对于承压含水层，解析解计算值与实际观测值误差不超过5.0%。对于水位降深变化相对于含水层厚度不可忽略的潜水类型场地，解析解计算值与实际观测值则偏离较大，相对误差为80.7%；水文地质条件数据充分时，数值模拟计算结果与实际观测偏离较小，相对误差为9.1%。
2)对于均质、等厚承压水类型场地，可采用解析解计算公式法来获取单井捕获半径及驻点，该方法简便快捷，获取值与实际观测值较为吻合；对于水位降深相对含水层厚度不可忽略的潜水类型场地，可采用数值模拟法来获取单井捕获半径及驻点值，水文地质条件掌握越充分，模拟结果与实际观测值越相符。
3)在获取捕获半径及驻点时，可优先考虑解析解计算公式法；当水文地质条件不符合公式假设条件时，依次考虑数值模拟法、抽水实验实测法。
单井捕获地下水污染羽的优化方法
Optimal method of groundwater pollution plume capture by single well
-
摘要: 针对不同抽水井捕获半径及驻点获取方法存在局限性和误差的问题，以潜水、承压水2个类型污染场地为例，分别采用实测法、解析解公式法、数值模拟法3种方法计算单井捕获半径及驻点值；通过对比分析，研究了不同条件下3种方法的局限性及精确度；探讨了不同类型污染场地获取捕获半径及驻点的最适宜方法。结果表明：对于承压水类型，解析解计算值与实际观测值误差较小，为3.2%；对于水位降深相对于含水层厚度不可忽略的潜水类型，解析解计算值与实际观测值误差较大，为80.7%；在充分掌握水文地质条件时，数值模型模拟结果与实际观测误差值不超过10%。因此，当场地水文地质情况符合解析解公式假设条件时，可采用解析解公式法获取单井捕获半径及驻点，否则须利用数值模拟方法或实测法获取相关参数。研究成果为不同类型污染场地选择合适方法获取捕获半径及驻点提供了参考。Abstract: In view of the limitations and errors in the acquisition methods of capture radius and stagnation points of different pumping wells, two types of contaminated sites, such as unconfined aquifer and confined aquifer, were taken as examples. Subsequently, the capture radius and stagnation point of a single well are calculated by using the measurement method, the analytical solution formula method and the numerical simulation method, respectively. Through comparative analysis, the limitations and accuracy of the three methods under different conditions were studied. The optimum methods for obtaining the capture radius and stagnation point of different types of contaminated sites were discussed. The results show that for the type of confined aquifer, a low error of 3.2% between the calculated value of analytical solution and the measured value occurred. For the type of unconfined aquifer, its groundwater level drawdown could not be ignored with respect to aquifer thickness, a relatively high error of 80.7% between the calculated value of analytical solution and the measured value occurred. When the hydrogeological conditions were fully mastered, the error between the numerical model simulation result and the measured value did not exceed 10%. Therefore, when the hydrogeological conditions in the field met the assumed conditions of the analytical solution formula, the analytical solution formula could be used to obtain the capture radius and stagnation point of a single well, otherwise, the numerical simulation or field measurement method should be used to obtain the relevant parameters. This study provides a reference for selecting suitable methods to obtain the capture radius and stagnation point of different types of contaminated sites.
-
Key words:
- pumping test method /
- analytic solution formula /
- numerical simulation /
- capture radius /
- stagnation point /
- optimum
-
-
图 2 承压含水层抽水前的等水位线
Figure 2. Contour of groundwater table before pumping in confined aquifer
图 4 潜水含水层抽水前的等水位线图
Figure 4. Contour of groundwater table before pumping in unconfined aquifer
图 5 潜水含水层抽水稳定后的等水位线图
Figure 5. Contour of groundwater table after pumping stability in unconfined aquifer
图 6 承压含水层污染场地单井捕获半径粒子追踪
Figure 6. Particle tracking of single well capture radius in contaminated sites of confined aquifer
图 8 潜水含水层污染场地单井捕获半径粒子追踪
Figure 8. Particle tracking of single well capture radius in contaminated sites of unconfined aquifer
表 1 不同方式获取抽水井捕获半径及驻点值的对比
Table 1. Comparison between the capture radius and stagnation points obtained by different methods
场地类型 参数类型 抽水流量/
(m3·d−1)抽水实验
实测值/m解析解公式
计算值/m数值模
拟值/m解析解公式
法误差值/%数值模拟法
误差值/%承压水类型 捕获半径 120 290 293.7 285 1.3 1.7 驻点 120 95 93.5 98 1.6 3.2 潜水类型 捕获半径 60 88 33.3 84 58.4 4.6 驻点 60 55 10.6 50 80.7 9.1 
下载: 导出CSV
-
[1] 姜烈, 何江涛, 姜永海, 等. 地下水硝酸盐污染抽出处理优化方法模拟研究[J]. 环境科学, 2014, 35(7): 2572-2578. [2] 王燕.硝酸盐地下水污染数值模拟与抽出-处理技术抽水井优化研究[D]. 保定: 河北农业大学, 2014. [3] 蒲敏. 污染场地地下水抽出处理技术研究[J]. 环境工程, 2017, 35(4): 6-10. [4] 万鹏.污染地下水抽出-处理技术的抽水方案优化研究[D]. 北京: 清华大学, 2013. [5] 张艳.污染场地抽出-处理技术影响因素及优化方案研究[D]. 北京: 中国地质大学(北京), 2010. [6] 任增平. 水力截获技术及其研究进展[J]. 水文地质工程地质, 2001(6): 73-77. doi: 10.3969/j.issn.1000-3665.2001.06.026 [7] JAVANDEL I, TSANG C. Capture-zone type curves: A tool for aquifer cleanup[J]. Groundwater, 1986, 24(5): 616-625. [8] GRUBB S. Analytical model for estimation of steady-state capture zones of pumping wells in confined and unconfined aquifers[J]. Groundwater, 1993, 31(1): 27-32. [9] ZLOTNIK V. A Effects of anisotropy on the capture zone of a partially penetrating well[J]. Groundwater, 1997, 35(5): 842-847. [10] BAIR E S, LAHM T D. Variations in capture-zone geometry of a partially penetrating pumping well in an unconfined aquifer[J]. Groundwater, 1996, 34(5): 842-852. [11] SATKIN R L, BEDIENT P B. Effectiveness of various aquifer restoration schemes under variable hydrogeologic conditions[J]. Groundwater, 1988, 26(4): 488-498. [12] KIM J W. Optimal pumping time for a pump-and-treat determined from radial convergent tracer tests[J]. Geosciences Journal, 2014, 18(1): 69-80. doi: 10.1007/s12303-013-0051-x [13] 刘明柱, 陈鸿汉, 胡丽琴, 等. 生物降解作用下地下水中TCE、PCE迁移转化的数值模拟研究[J]. 地学前缘, 2006, 13(1): 155-159. doi: 10.3321/j.issn:1005-2321.2006.01.021 [14] 于虎广. 基于Visual Modflow的曲周县地下水中盐分运移模拟研究[D]. 邯郸: 河北工程大学, 2012. [15] 陈崇希, 王旭升, 胡立堂. 地下水流数值模拟中抽水井水位的校正[J]. 水利学报, 2007, 38(4): 481-485. doi: 10.3321/j.issn:0559-9350.2007.04.016 [16] 张海岛.长治盆地浅层孔隙地下水流数值模拟研究[D]. 邯郸: 河北工程大学, 2017. [17] 白福高, 刘明柱, 刘伟江, 等. 潮白河河道地下水人工回灌包气带水分运移模拟[J]. 环境污染与防治, 2016, 38(6): 88-91. [18] 刘燕, 辛璐君, 郭建青, 等. 抽水实验确定各向异性含水层参数的实例讨论[J]. 勘察科学技术, 2012(6): 5-9. doi: 10.3969/j.issn.1001-3946.2012.06.002 [19] 蒋辉. 基于Aquifer Test的抽水实验参数计算方法分析[J]. 水文地质工程地质, 2011, 38(2): 35-38. doi: 10.3969/j.issn.1000-3665.2011.02.006 [20] 中华人民共和国水利部发布. 中华人民共和国水利行业标准水利水电工程钻孔抽水试验规程: SL 320-2005[M]. 北京: 中国水利水电出版社, 2005. -
点击查看大图
计量
- 文章访问数: 4690
- HTML全文浏览数: 4690
- PDF下载数: 80
- 施引文献: 0
